Intro
Discover 5 ways to apply Spearmans rank in Excel, enhancing data analysis with non-parametric stats, correlation, and ranking methods.
The importance of statistical analysis in today's data-driven world cannot be overstated. With the vast amount of data being generated every day, it's crucial to have the right tools and techniques to make sense of it all. One such technique is Spearman's rank correlation, a non-parametric measure of correlation that assesses the relationship between two variables. In this article, we'll explore the concept of Spearman's rank correlation and how to calculate it in Excel, a popular spreadsheet software used by millions of people around the world.
Spearman's rank correlation is a powerful tool for analyzing data, especially when dealing with ordinal or ranked data. It's widely used in various fields, including social sciences, medicine, and finance. The technique is named after Charles Spearman, who developed it in the early 20th century. In essence, Spearman's rank correlation measures the strength and direction of the relationship between two variables, taking into account the ranks of the data points rather than their actual values.
The use of Excel in data analysis is ubiquitous, and for good reason. Its intuitive interface, powerful formulas, and extensive range of functions make it an ideal tool for data manipulation and analysis. When it comes to calculating Spearman's rank correlation, Excel provides several methods, including the use of formulas, functions, and add-ins. In this article, we'll delve into the details of each method, providing step-by-step instructions and examples to help you get started.
What is Spearman's Rank Correlation?

- ρ = 1 indicates a perfect positive correlation
- ρ = -1 indicates a perfect negative correlation
- ρ = 0 indicates no correlation
The interpretation of the Spearman's rank correlation coefficient is similar to that of the Pearson correlation coefficient, but with a few key differences. While Pearson's correlation is sensitive to outliers and assumes a linear relationship between the variables, Spearman's rank correlation is more robust and can handle non-linear relationships.
Calculating Spearman's Rank Correlation in Excel

- Using the CORREL function: The CORREL function in Excel can be used to calculate the Pearson correlation coefficient, which can then be converted to the Spearman's rank correlation coefficient using a simple formula.
- Using the RANK function: The RANK function in Excel can be used to rank the data points for each variable, and then calculate the Spearman's rank correlation coefficient using the ranked data.
- Using an add-in: There are several add-ins available for Excel that provide a Spearman's rank correlation function, including the Analysis ToolPak and the Real Statistics add-in.
Each method has its advantages and disadvantages, and the choice of method will depend on the specific requirements of the analysis.
Method 1: Using the CORREL Function

ρ = 1 - (6 * Σd^2) / (n^3 - n)
where:
- ρ is the Spearman's rank correlation coefficient
- d is the difference between the ranks of the two variables
- n is the number of data points
To calculate the Spearman's rank correlation coefficient using the CORREL function, follow these steps:
- Enter the data for the two variables in two separate columns.
- Calculate the ranks for each variable using the RANK function.
- Calculate the differences between the ranks using the formula: d = rank_X - rank_Y
- Calculate the sum of the squared differences using the formula: Σd^2 = Σ(d^2)
- Calculate the Spearman's rank correlation coefficient using the formula: ρ = 1 - (6 * Σd^2) / (n^3 - n)
Method 2: Using the RANK Function
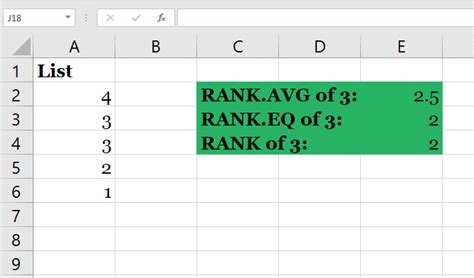
- Enter the data for the two variables in two separate columns.
- Calculate the ranks for each variable using the RANK function.
- Calculate the Spearman's rank correlation coefficient using the formula: ρ = 1 - (6 * Σd^2) / (n^3 - n)
where:
- ρ is the Spearman's rank correlation coefficient
- d is the difference between the ranks of the two variables
- n is the number of data points
Method 3: Using an Add-in

To calculate the Spearman's rank correlation coefficient using an add-in, follow these steps:
- Install the add-in and activate it in Excel.
- Enter the data for the two variables in two separate columns.
- Select the data range and click on the add-in's function to calculate the Spearman's rank correlation coefficient.
Gallery of Spearman's Rank Correlation Images
Spearman's Rank Correlation Image Gallery
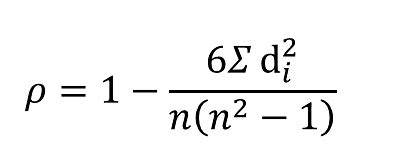



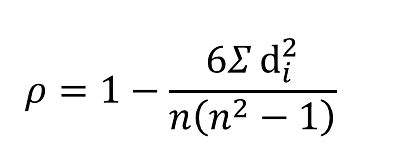

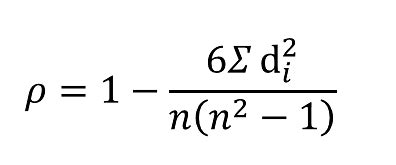

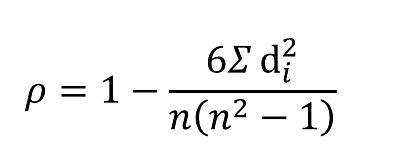

Frequently Asked Questions
What is Spearman's rank correlation?
+Spearman's rank correlation is a statistical measure that assesses the relationship between two variables, typically denoted as X and Y. The technique involves ranking the data points for each variable, and then calculating the correlation coefficient based on these ranks.
How do I calculate Spearman's rank correlation in Excel?
+There are several ways to calculate Spearman's rank correlation in Excel, including using the CORREL function, the RANK function, or an add-in. The choice of method will depend on the specific requirements of the analysis.
What is the difference between Spearman's rank correlation and Pearson's correlation?
+Spearman's rank correlation is a non-parametric measure of correlation that assesses the relationship between two variables based on their ranks, while Pearson's correlation is a parametric measure that assesses the relationship between two variables based on their actual values. Spearman's rank correlation is more robust and can handle non-linear relationships, while Pearson's correlation is sensitive to outliers and assumes a linear relationship.
In conclusion, Spearman's rank correlation is a powerful tool for analyzing data, especially when dealing with ordinal or ranked data. The technique is widely used in various fields, including social sciences, medicine, and finance. By understanding the concept of Spearman's rank correlation and how to calculate it in Excel, you can gain valuable insights into the relationships between variables and make informed decisions. Whether you're a student, researcher, or professional, mastering Spearman's rank correlation is an essential skill for anyone working with data. So why not give it a try? With the methods and examples outlined in this article, you'll be well on your way to becoming a proficient user of Spearman's rank correlation in Excel. Share your thoughts and experiences with us in the comments below, and don't forget to share this article with your friends and colleagues who may benefit from it.