Black Scholes Formula In Excel

The Black Scholes formula is a widely used mathematical model in finance that estimates the value of a call option or a put option. The formula is named after its creators, Fischer Black and Myron Scholes, who first introduced it in their 1973 paper "The Pricing of Options and Corporate Liabilities." The Black Scholes formula is a complex mathematical equation that takes into account various factors, including the current stock price, the strike price of the option, the time to expiration, the risk-free interest rate, and the volatility of the underlying asset. In this article, we will explore how to implement the Black Scholes formula in Excel, a popular spreadsheet software.

The Black Scholes formula is an essential tool for investors, traders, and financial analysts who need to estimate the value of options. The formula is based on several assumptions, including the idea that the price of the underlying asset follows a geometric Brownian motion, and that the risk-free interest rate is constant. While these assumptions may not always hold true in reality, the Black Scholes formula remains a widely accepted and useful tool for estimating option values.

To implement the Black Scholes formula in Excel, we need to use several functions, including the NORM.S.DIST function, which calculates the cumulative distribution function of the standard normal distribution. We also need to use the EXP function, which calculates the exponential of a given number. Additionally, we need to use the SQRT function, which calculates the square root of a given number.

Black Scholes Formula

The Black Scholes formula for a call option is given by the following equation:

C(S, t) = S * N(d1) - K * exp(-r * t) * N(d2)

Where:

C(S, t) is the value of the call option
S is the current stock price
K is the strike price of the option
r is the risk-free interest rate
t is the time to expiration
N(d1) and N(d2) are the cumulative distribution functions of the standard normal distribution
d1 and d2 are calculated using the following equations:

d1 = (ln(S / K) + (r + σ^2 / 2) * t) / (σ * sqrt(t)) d2 = d1 - σ * sqrt(t)

Where σ is the volatility of the underlying asset.

Implementing the Black Scholes Formula in Excel

To implement the Black Scholes formula in Excel, we can use the following steps:

Create a new spreadsheet and enter the following data:
- Current stock price (S)
- Strike price of the option (K)
- Risk-free interest rate (r)
- Time to expiration (t)
- Volatility of the underlying asset (σ)
Calculate d1 and d2 using the following equations:
- d1 = (LN(S / K) + (r + σ^2 / 2) * t) / (σ * SQRT(t))
- d2 = d1 - σ * SQRT(t)
Calculate N(d1) and N(d2) using the NORM.S.DIST function:
- N(d1) = NORM.S.DIST(d1, TRUE)
- N(d2) = NORM.S.DIST(d2, TRUE)
Calculate the value of the call option using the following equation:
- C(S, t) = S * N(d1) - K * EXP(-r * t) * N(d2)

Example Calculation

Let's say we want to calculate the value of a call option with the following parameters:

Current stock price (S) = $100
Strike price of the option (K) = $110
Risk-free interest rate (r) = 5%
Time to expiration (t) = 1 year
Volatility of the underlying asset (σ) = 20%

Using the steps outlined above, we can calculate the value of the call option as follows:

Calculate d1 and d2:
- d1 = (LN(100 / 110) + (0.05 + 0.2^2 / 2) * 1) / (0.2 * SQRT(1)) = -0.514
- d2 = d1 - 0.2 * SQRT(1) = -0.714
Calculate N(d1) and N(d2):
- N(d1) = NORM.S.DIST(-0.514, TRUE) = 0.303
- N(d2) = NORM.S.DIST(-0.714, TRUE) = 0.237
Calculate the value of the call option:
- C(S, t) = 100 * 0.303 - 110 * EXP(-0.05 * 1) * 0.237 = $10.31

Black Scholes Formula for Put Options

The Black Scholes formula for put options is similar to the formula for call options, but with some key differences. The formula for a put option is given by the following equation:

P(S, t) = K * exp(-r * t) * N(-d2) - S * N(-d1)

Where:

P(S, t) is the value of the put option
S is the current stock price
K is the strike price of the option
r is the risk-free interest rate
t is the time to expiration
N(d1) and N(d2) are the cumulative distribution functions of the standard normal distribution
d1 and d2 are calculated using the same equations as before

Implementing the Black Scholes Formula for Put Options in Excel

To implement the Black Scholes formula for put options in Excel, we can use the following steps:

Create a new spreadsheet and enter the following data:
- Current stock price (S)
- Strike price of the option (K)
- Risk-free interest rate (r)
- Time to expiration (t)
- Volatility of the underlying asset (σ)
Calculate d1 and d2 using the same equations as before:
- d1 = (LN(S / K) + (r + σ^2 / 2) * t) / (σ * SQRT(t))
- d2 = d1 - σ * SQRT(t)
Calculate N(d1) and N(d2) using the NORM.S.DIST function:
- N(d1) = NORM.S.DIST(d1, TRUE)
- N(d2) = NORM.S.DIST(d2, TRUE)
Calculate the value of the put option using the following equation:
- P(S, t) = K * EXP(-r * t) * N(-d2) - S * N(-d1)

Example Calculation for Put Options

Let's say we want to calculate the value of a put option with the same parameters as before:

Current stock price (S) = $100
Strike price of the option (K) = $110
Risk-free interest rate (r) = 5%
Time to expiration (t) = 1 year
Volatility of the underlying asset (σ) = 20%

Using the steps outlined above, we can calculate the value of the put option as follows:

Calculate d1 and d2:
- d1 = (LN(100 / 110) + (0.05 + 0.2^2 / 2) * 1) / (0.2 * SQRT(1)) = -0.514
- d2 = d1 - 0.2 * SQRT(1) = -0.714
Calculate N(d1) and N(d2):
- N(d1) = NORM.S.DIST(-0.514, TRUE) = 0.303
- N(d2) = NORM.S.DIST(-0.714, TRUE) = 0.237
Calculate the value of the put option:
- P(S, t) = 110 * EXP(-0.05 * 1) * N(-(-0.714)) - 100 * N(-(-0.514)) = $14.19

Gallery of Black Scholes Formula

Black Scholes Formula Image Gallery

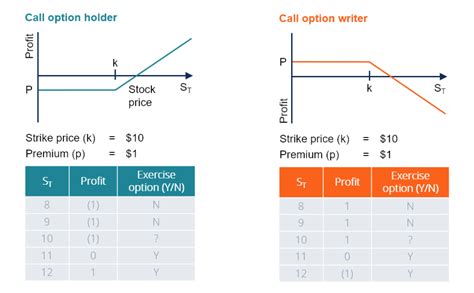
Frequently Asked Questions

What is the Black Scholes formula?

The Black Scholes formula is a mathematical model used to estimate the value of a call option or a put option.

How do I implement the Black Scholes formula in Excel?

To implement the Black Scholes formula in Excel, you need to use the NORM.S.DIST function, the EXP function, and the SQRT function. You also need to enter the current stock price, the strike price of the option, the risk-free interest rate, the time to expiration, and the volatility of the underlying asset.

What are the limitations of the Black Scholes formula?

The Black Scholes formula has several limitations, including the assumption that the price of the underlying asset follows a geometric Brownian motion, and that the risk-free interest rate is constant. Additionally, the formula does not take into account dividends, transaction costs, or other factors that can affect the value of an option.

How do I use the Black Scholes formula to estimate the value of a put option?

To estimate the value of a put option using the Black Scholes formula, you need to use the same equations as for a call option, but with some key differences. You need to calculate the value of the put option using the formula P(S, t) = K \* EXP(-r \* t) \* N(-d2) - S \* N(-d1).

What are some common applications of the Black Scholes formula?

The Black Scholes formula has several common applications, including options pricing, financial modeling, and risk management. It is widely used by investors, traders, and financial analysts to estimate the value of options and to make informed investment decisions.

Final Thoughts

the Black Scholes formula is a powerful tool for estimating the value of options. While it has several limitations, it remains a widely accepted and useful model for investors, traders, and financial analysts. By understanding how to implement the Black Scholes formula in Excel, you can make more informed investment decisions and better manage your risk. We hope this article has provided you with a comprehensive overview of the Black Scholes formula and its applications. If you have any questions or comments, please feel free to share them with us. Additionally, if you found this article helpful, please share it with others who may be interested in learning more about the Black Scholes formula.