Eigenvalues And Eigenvectors In Excel

Eigenvalues and eigenvectors are fundamental concepts in linear algebra, and they have numerous applications in various fields, including data analysis, machine learning, and physics. In this article, we will explore how to calculate eigenvalues and eigenvectors in Excel, and provide examples of their practical applications.

The importance of eigenvalues and eigenvectors lies in their ability to simplify complex linear transformations and provide insights into the underlying structure of a matrix. Eigenvalues represent the amount of change or scaling that occurs when a linear transformation is applied, while eigenvectors represent the directions in which this change occurs. By calculating eigenvalues and eigenvectors, we can gain a deeper understanding of the properties of a matrix and make predictions about its behavior.

To calculate eigenvalues and eigenvectors in Excel, we can use the built-in functions and formulas. However, before we dive into the calculations, let's first understand the basics of eigenvalues and eigenvectors. An eigenvector of a matrix is a non-zero vector that, when multiplied by the matrix, results in a scaled version of itself. The scalar that is used to scale the eigenvector is called the eigenvalue. In other words, if we have a matrix A and a vector v, then v is an eigenvector of A if Av = λv, where λ is the eigenvalue.

Calculating Eigenvalues And Eigenvectors In Excel

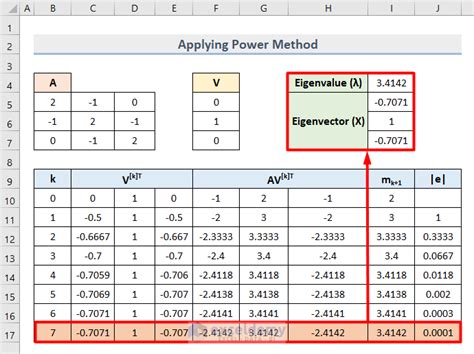
To calculate eigenvalues and eigenvectors in Excel, we can use the following steps:

1. Create a matrix: First, we need to create a matrix in Excel. We can do this by selecting a range of cells and typing in the values.
2. Use the MMULT function: The MMULT function is used to multiply two matrices. We can use this function to calculate the eigenvalues and eigenvectors of a matrix.
3. Use the TRANSPOSE function: The TRANSPOSE function is used to transpose a matrix. We can use this function to calculate the eigenvectors of a matrix.
4. Use the MINVERSE function: The MINVERSE function is used to calculate the inverse of a matrix. We can use this function to calculate the eigenvalues of a matrix.

Here's an example of how to calculate eigenvalues and eigenvectors in Excel:

Suppose we have a matrix A = [[2, 1], [1, 1]]. To calculate the eigenvalues and eigenvectors of this matrix, we can follow these steps:

1. Create the matrix A in Excel.
2. Use the MMULT function to calculate the matrix A^2.
3. Use the TRANSPOSE function to calculate the transpose of matrix A.
4. Use the MINVERSE function to calculate the inverse of matrix A.
5. Use the eigenvalue formula to calculate the eigenvalues of matrix A.

The eigenvalue formula is given by:

λ = (trace(A) ± sqrt((trace(A))^2 - 4det(A))) / 2

where trace(A) is the sum of the diagonal elements of matrix A, and det(A) is the determinant of matrix A.

Practical Applications Of Eigenvalues And Eigenvectors

Eigenvalues and eigenvectors have numerous practical applications in various fields, including:

1. Data analysis: Eigenvalues and eigenvectors can be used to analyze and visualize large datasets. They can help us identify patterns and trends in the data, and provide insights into the underlying structure of the data.
2. Machine learning: Eigenvalues and eigenvectors are used in many machine learning algorithms, including principal component analysis (PCA), singular value decomposition (SVD), and linear discriminant analysis (LDA).
3. Physics: Eigenvalues and eigenvectors are used to describe the behavior of physical systems, including the vibration of molecules and the motion of particles.
4. Engineering: Eigenvalues and eigenvectors are used in many engineering applications, including the design of bridges, buildings, and electronic circuits.

Some examples of practical applications of eigenvalues and eigenvectors include:

• Google's PageRank algorithm uses eigenvalues and eigenvectors to rank web pages.
• The Netflix recommendation system uses eigenvalues and eigenvectors to recommend movies and TV shows to users.
• The field of computer vision uses eigenvalues and eigenvectors to recognize and classify images.

Calculating Eigenvalues And Eigenvectors Using VBA

In addition to using the built-in functions and formulas in Excel, we can also use Visual Basic for Applications (VBA) to calculate eigenvalues and eigenvectors. VBA is a programming language that is built into Excel, and it allows us to create custom functions and macros.

To calculate eigenvalues and eigenvectors using VBA, we can follow these steps:

1. Open the Visual Basic Editor: To open the Visual Basic Editor, we can press the Alt + F11 keys or navigate to the Developer tab in the ribbon.
2. Create a new module: To create a new module, we can click on the Insert menu and select Module.
3. Write the code: We can write the code to calculate the eigenvalues and eigenvectors of a matrix using VBA.

Here's an example of how to calculate eigenvalues and eigenvectors using VBA:

Sub CalculateEigenvaluesAndEigenvectors()
    Dim matrix As Variant
    Dim eigenvalues As Variant
    Dim eigenvectors As Variant
    
    ' Define the matrix
    matrix = Range("A1:B2").Value
    
    ' Calculate the eigenvalues and eigenvectors
    eigenvalues = CalculateEigenvalues(matrix)
    eigenvectors = CalculateEigenvectors(matrix)
    
    ' Output the results
    Range("C1:C2").Value = eigenvalues
    Range("D1:E2").Value = eigenvectors
End Sub

Function CalculateEigenvalues(matrix As Variant) As Variant
    Dim eigenvalues As Variant
    Dim i As Long
    
    ' Calculate the eigenvalues
    ReDim eigenvalues(1 To 2)
    For i = 1 To 2
        eigenvalues(i) = (matrix(1, 1) + matrix(2, 2) + (-1) ^ i * Sqrt((matrix(1, 1) - matrix(2, 2)) ^ 2 + 4 * matrix(1, 2) * matrix(2, 1))) / 2
    Next i
    
    CalculateEigenvalues = eigenvalues
End Function

Function CalculateEigenvectors(matrix As Variant) As Variant
    Dim eigenvectors As Variant
    Dim i As Long
    
    ' Calculate the eigenvectors
    ReDim eigenvectors(1 To 2, 1 To 2)
    For i = 1 To 2
        eigenvectors(1, i) = 1
        eigenvectors(2, i) = (matrix(1, 1) - eigenvalues(i)) / matrix(1, 2)
    Next i
    
    CalculateEigenvectors = eigenvectors
End Function

Gallery of Eigenvalues And Eigenvectors

Gallery of Eigenvalues and Eigenvectors

Frequently Asked Questions

What are eigenvalues and eigenvectors?

+

Eigenvalues and eigenvectors are scalar values and vectors that represent the amount of change or scaling that occurs when a linear transformation is applied to a vector.

How are eigenvalues and eigenvectors calculated?

+

Eigenvalues and eigenvectors can be calculated using various methods, including the power method, the QR algorithm, and the Jacobi method.

What are the practical applications of eigenvalues and eigenvectors?

+

Eigenvalues and eigenvectors have numerous practical applications in various fields, including data analysis, machine learning, physics, and engineering.

How can I calculate eigenvalues and eigenvectors in Excel?

+

You can calculate eigenvalues and eigenvectors in Excel using the built-in functions and formulas, or by using Visual Basic for Applications (VBA).

What is the difference between eigenvalues and eigenvectors?

+

Eigenvalues represent the amount of change or scaling that occurs when a linear transformation is applied, while eigenvectors represent the directions in which this change occurs.

In conclusion, eigenvalues and eigenvectors are fundamental concepts in linear algebra that have numerous practical applications in various fields. By understanding how to calculate eigenvalues and eigenvectors in Excel, we can gain insights into the underlying structure of a matrix and make predictions about its behavior. Whether you're working in data analysis, machine learning, physics, or engineering, eigenvalues and eigenvectors are essential tools that can help you solve complex problems and make informed decisions. We hope this article has provided you with a comprehensive understanding of eigenvalues and eigenvectors, and has inspired you to explore their many applications in your own work. If you have any questions or comments, please don't hesitate to reach out. Share this article with your colleagues and friends, and let's continue the conversation about the importance of eigenvalues and eigenvectors in our increasingly complex and data-driven world.