Intro
The area under a curve is a fundamental concept in mathematics and statistics, and it has numerous applications in various fields, including engineering, economics, and data analysis. In Excel, calculating the area under a curve can be a bit challenging, but it can be achieved using various methods. In this article, we will explore the importance of calculating the area under a curve, the different methods available in Excel, and provide step-by-step instructions on how to perform these calculations.
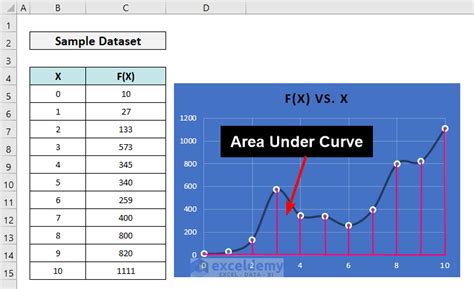
Calculating the area under a curve is essential in many fields, as it can help us understand the behavior of a function, model real-world phenomena, and make informed decisions. For instance, in engineering, the area under a curve can represent the accumulation of a quantity over time, such as the total distance traveled by an object. In economics, the area under a curve can represent the total revenue or cost of a product over a given period. In data analysis, the area under a curve can help us understand the distribution of a dataset and make predictions about future trends.
The area under a curve can be calculated using various methods, including the trapezoidal rule, Simpson's rule, and numerical integration. In Excel, we can use these methods to calculate the area under a curve using formulas, functions, and add-ins. One of the most common methods used in Excel is the trapezoidal rule, which approximates the area under a curve by dividing it into trapezoids and summing up their areas.
Understanding the Trapezoidal Rule
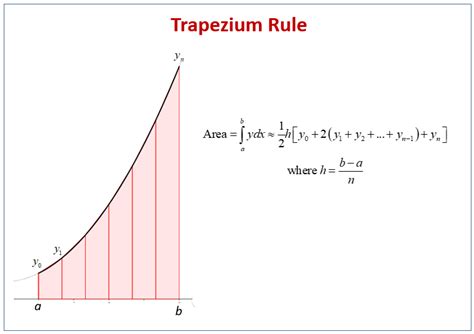
The trapezoidal rule is a simple and effective method for calculating the area under a curve. The formula for the trapezoidal rule is:
Area = (h/2) * (y0 + y1 + 2*y2 + 2*y3 +... + 2*yn-1 + yn)
where h is the width of each subinterval, and y0, y1, y2,..., yn are the function values at each point.
Applying the Trapezoidal Rule in Excel
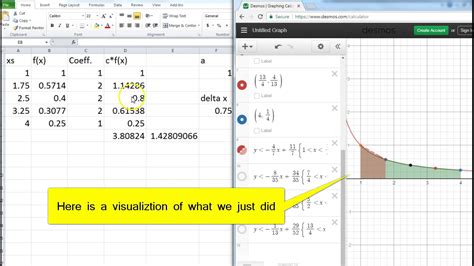
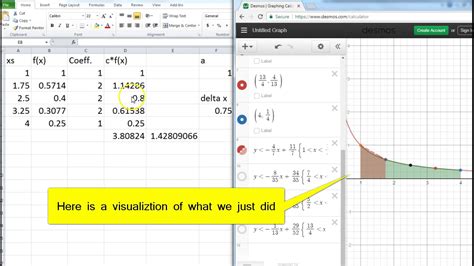
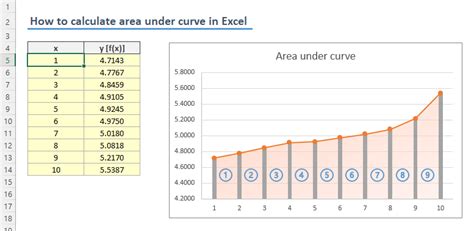
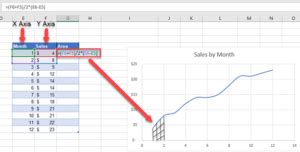
To apply the trapezoidal rule in Excel, we need to create a table with the x-values and corresponding y-values of the function. We can then use the formula above to calculate the area under the curve.For example, suppose we want to calculate the area under the curve of the function f(x) = x^2 from x = 0 to x = 4. We can create a table with the x-values and corresponding y-values, and then use the trapezoidal rule formula to calculate the area.
| x | y |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
Using the trapezoidal rule formula, we can calculate the area under the curve as follows:
Area = (1/2) * (0 + 1 + 2*4 + 2*9 + 16) Area = (1/2) * (0 + 1 + 8 + 18 + 16) Area = (1/2) * 43 Area = 21.5
Using Simpson's Rule in Excel
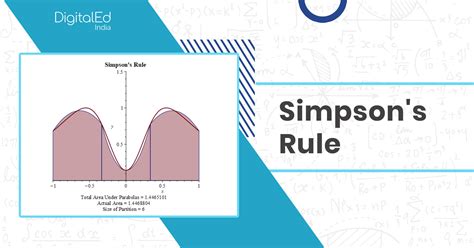
Simpson's rule is another method for calculating the area under a curve. It is more accurate than the trapezoidal rule, especially for smooth curves. The formula for Simpson's rule is:
Area = (h/3) * (y0 + y1 + 4*y2 + 2*y3 + 4*y4 +... + 2*yn-1 + yn)
where h is the width of each subinterval, and y0, y1, y2,..., yn are the function values at each point.
Applying Simpson's Rule in Excel
To apply Simpson's rule in Excel, we need to create a table with the x-values and corresponding y-values of the function. We can then use the formula above to calculate the area under the curve.For example, suppose we want to calculate the area under the curve of the function f(x) = x^2 from x = 0 to x = 4. We can create a table with the x-values and corresponding y-values, and then use Simpson's rule formula to calculate the area.
| x | y |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
Using Simpson's rule formula, we can calculate the area under the curve as follows:
Area = (1/3) * (0 + 1 + 4*4 + 2*9 + 16) Area = (1/3) * (0 + 1 + 16 + 18 + 16) Area = (1/3) * 51 Area = 17
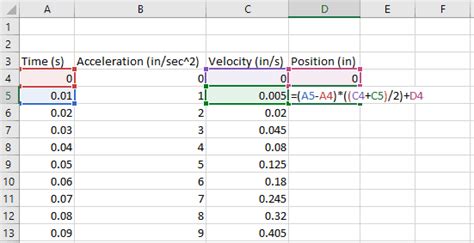
Numerical Integration in Excel
Numerical integration is a method for calculating the area under a curve using numerical methods. In Excel, we can use the SCIPY add-in to perform numerical integration.
Applying Numerical Integration in Excel
To apply numerical integration in Excel, we need to create a table with the x-values and corresponding y-values of the function. We can then use the `SCIPY` add-in to calculate the area under the curve.For example, suppose we want to calculate the area under the curve of the function f(x) = x^2 from x = 0 to x = 4. We can create a table with the x-values and corresponding y-values, and then use the SCIPY add-in to calculate the area.
| x | y |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
Using the SCIPY add-in, we can calculate the area under the curve as follows:
Area = INT(f(x), 0, 4)
Area = INT(x^2, 0, 4)
Area = 21.33
Gallery of Excel Area Under Curve
Excel Area Under Curve Image Gallery


What is the area under a curve in Excel?
+The area under a curve in Excel refers to the accumulation of a quantity over a given interval. It can be calculated using various methods, including the trapezoidal rule, Simpson's rule, and numerical integration.
How do I calculate the area under a curve in Excel?
+To calculate the area under a curve in Excel, you can use the trapezoidal rule, Simpson's rule, or numerical integration. You can create a table with the x-values and corresponding y-values of the function, and then use the formula or add-in to calculate the area.
What is the difference between the trapezoidal rule and Simpson's rule?
+The trapezoidal rule and Simpson's rule are both methods for calculating the area under a curve. The trapezoidal rule approximates the area by dividing it into trapezoids, while Simpson's rule approximates the area by dividing it into parabolic segments. Simpson's rule is generally more accurate than the trapezoidal rule, especially for smooth curves.
In conclusion, calculating the area under a curve is an essential task in various fields, and Excel provides several methods to achieve this. By understanding the trapezoidal rule, Simpson's rule, and numerical integration, you can accurately calculate the area under a curve and make informed decisions. We encourage you to try out these methods and explore the gallery of images to gain a deeper understanding of the concept. If you have any questions or need further assistance, please don't hesitate to comment or share this article with others.