Area Under Curve In Excel

The area under a curve is a fundamental concept in mathematics and statistics, and it has numerous applications in various fields, including engineering, economics, and physics. In Excel, calculating the area under a curve can be a bit tricky, but it is definitely possible. In this article, we will explore the importance of calculating the area under a curve, and we will provide a step-by-step guide on how to do it in Excel.

Calculating the area under a curve is essential in many real-world applications. For instance, in engineering, it is used to calculate the volume of a solid, the length of a curve, or the surface area of a shape. In economics, it is used to calculate the total cost or revenue of a company over a given period. In physics, it is used to calculate the work done by a force or the energy transferred between systems. The area under a curve can also be used to model population growth, chemical reactions, and electrical circuits.

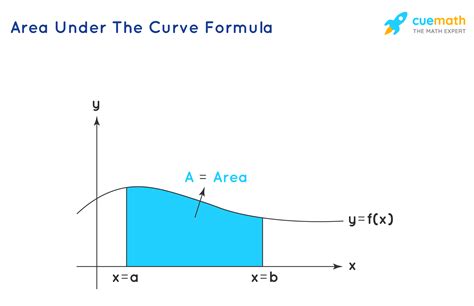
The concept of area under a curve is based on the definite integral, which is a fundamental concept in calculus. The definite integral of a function f(x) from a to b is denoted as ∫[a,b] f(x) dx, and it represents the area under the curve of f(x) between the limits a and b. In Excel, we can calculate the area under a curve using various methods, including the trapezoidal rule, Simpson's rule, and numerical integration.

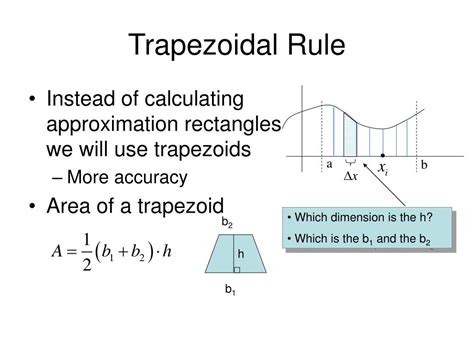
Understanding the Trapezoidal Rule

The trapezoidal rule is a simple method for approximating the area under a curve. It works by dividing the area under the curve into small trapezoids and summing up the areas of these trapezoids. The formula for the trapezoidal rule is: ∫[a,b] f(x) dx ≈ (h/2) \* (f(a) + f(b) + 2\*∑[f(x_i)]), where h is the width of each subinterval, and x_i are the points in the subinterval.

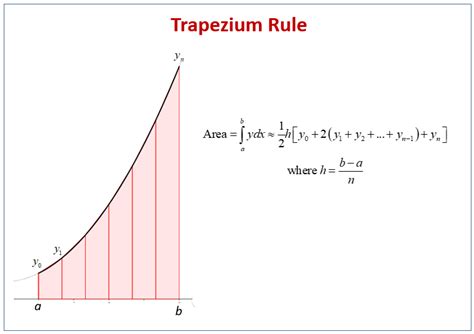
Applying the Trapezoidal Rule in Excel

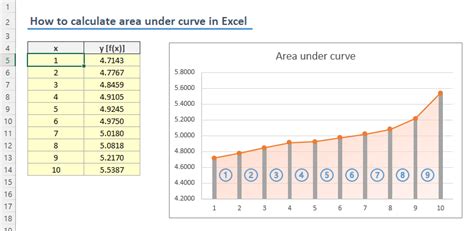
To apply the trapezoidal rule in Excel, we need to create a table with the x-values and corresponding y-values of the function. We can then use the formula =((x2-x1)/2)\*(y1+y2) to calculate the area of each trapezoid, where x1 and x2 are the x-values of the subinterval, and y1 and y2 are the corresponding y-values. We can then sum up the areas of all the trapezoids to get the total area under the curve.

Using Simpson's Rule

Simpson's rule is another method for approximating the area under a curve. It works by dividing the area under the curve into small parabolic segments and summing up the areas of these segments. The formula for Simpson's rule is: ∫[a,b] f(x) dx ≈ (h/3) \* (f(a) + f(b) + 4\*∑[f(x_i)] + 2\*∑[f(x_j)]), where h is the width of each subinterval, x_i are the points in the subinterval, and x_j are the points at the midpoint of each subinterval.

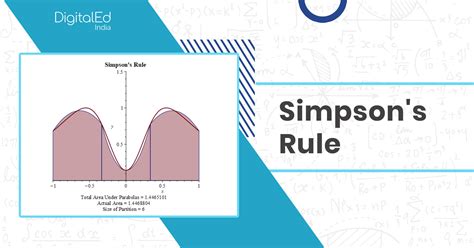
Applying Simpson's Rule in Excel

To apply Simpson's rule in Excel, we need to create a table with the x-values and corresponding y-values of the function. We can then use the formula =((x2-x1)/3)\*(y1+4\*y2+y3) to calculate the area of each parabolic segment, where x1, x2, and x3 are the x-values of the subinterval, and y1, y2, and y3 are the corresponding y-values. We can then sum up the areas of all the parabolic segments to get the total area under the curve.

Numerical Integration

Numerical integration is a method for approximating the area under a curve using numerical methods. It works by dividing the area under the curve into small subintervals and approximating the area of each subinterval using a numerical method such as the trapezoidal rule or Simpson's rule. In Excel, we can use the `SCIPY` library to perform numerical integration.

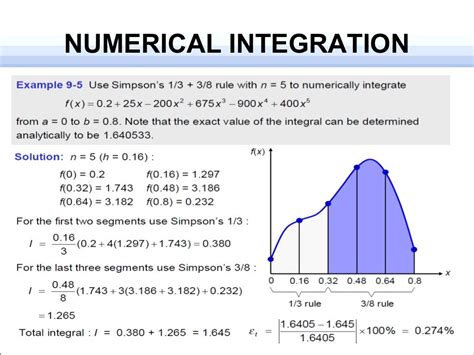
Using the SCIPY Library in Excel

To use the `SCIPY` library in Excel, we need to install the `SCIPY` add-in and then use the `quad` function to perform numerical integration. The `quad` function takes two arguments: the function to integrate and the limits of integration. We can then use the `quad` function to calculate the area under the curve.

Practical Examples

Let's consider a few practical examples of calculating the area under a curve in Excel. Suppose we want to calculate the area under the curve of the function f(x) = x^2 from x = 0 to x = 4. We can use the trapezoidal rule, Simpson's rule, or numerical integration to calculate the area.

Example 1: Trapezoidal Rule

To calculate the area under the curve using the trapezoidal rule, we can create a table with the x-values and corresponding y-values of the function. We can then use the formula =((x2-x1)/2)\*(y1+y2) to calculate the area of each trapezoid. We can then sum up the areas of all the trapezoids to get the total area under the curve.

Example 2: Simpson's Rule

To calculate the area under the curve using Simpson's rule, we can create a table with the x-values and corresponding y-values of the function. We can then use the formula =((x2-x1)/3)\*(y1+4\*y2+y3) to calculate the area of each parabolic segment. We can then sum up the areas of all the parabolic segments to get the total area under the curve.

Example 3: Numerical Integration

To calculate the area under the curve using numerical integration, we can use the `SCIPY` library in Excel. We can install the `SCIPY` add-in and then use the `quad` function to perform numerical integration. The `quad` function takes two arguments: the function to integrate and the limits of integration. We can then use the `quad` function to calculate the area under the curve.

Area Under Curve Image Gallery

What is the area under a curve?

+

The area under a curve is the region bounded by the curve, the x-axis, and the limits of integration.

How do I calculate the area under a curve in Excel?

+

You can calculate the area under a curve in Excel using the trapezoidal rule, Simpson's rule, or numerical integration.

What is the trapezoidal rule?

+

The trapezoidal rule is a method for approximating the area under a curve by dividing the area into small trapezoids and summing up the areas of these trapezoids.

What is Simpson's rule?

+

Simpson's rule is a method for approximating the area under a curve by dividing the area into small parabolic segments and summing up the areas of these segments.

What is numerical integration?

+

Numerical integration is a method for approximating the area under a curve using numerical methods such as the trapezoidal rule or Simpson's rule.

In conclusion, calculating the area under a curve is an essential concept in mathematics and statistics, and it has numerous applications in various fields. In Excel, we can calculate the area under a curve using the trapezoidal rule, Simpson's rule, or numerical integration. We hope this article has provided you with a comprehensive guide on how to calculate the area under a curve in Excel. If you have any questions or need further clarification, please don't hesitate to comment below. We would be happy to help. Additionally, if you found this article helpful, please share it with your friends and colleagues who may benefit from it. Thank you for reading!