Calculate Z Score Excel

Intro

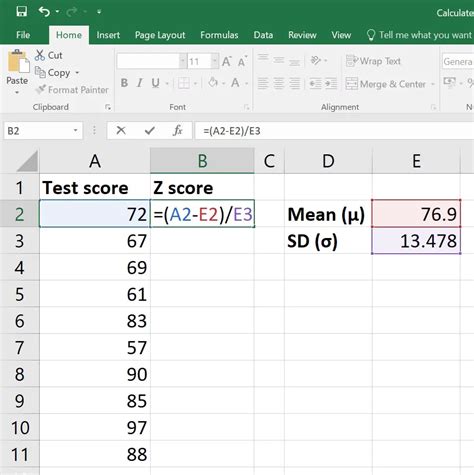
Calculating the Z score in Excel is a straightforward process that can be accomplished using a simple formula or through the use of built-in functions, depending on the version of Excel you are using. The Z score, also known as the standard score, is a measure of how many standard deviations an element is from the mean. It is calculated using the formula: Z = (X - μ) / σ, where X is the value of the element, μ is the mean of the dataset, and σ is the standard deviation.

In many cases, calculating the Z score is useful for understanding how a specific data point compares to the average of a dataset, taking into account the variability of the dataset. This can be particularly useful in statistical analysis, quality control, and data interpretation.

Using the Basic Formula

To calculate the Z score manually in Excel, you first need to know the mean (average) and standard deviation of your dataset. Here’s how you can do it:

  1. Calculate the Mean (μ):

    • Select a cell where you want to display the mean.
    • Type =AVERAGE(range) where "range" is the range of cells containing your data. For example, if your data is in cells A1 through A10, you would type =AVERAGE(A1:A10) and press Enter.

  2. Calculate the Standard Deviation (σ):

    • For a sample standard deviation, use the formula =STDEV.S(range).
    • For a population standard deviation, use =STDEV.P(range).
    • Replace "range" with the actual range of your data.

  3. Calculate the Z Score:

    • Select a cell where you want to display the Z score.
    • Type =(X - μ) / σ, where X is the value for which you want to calculate the Z score, μ is the cell containing the mean, and σ is the cell containing the standard deviation.
    • For example, if the value X is in cell A1, the mean μ is in cell B1, and the standard deviation σ is in cell C1, the formula would be =(A1-B1)/C1.

Using Built-in Functions

Excel 2013 and later versions include the Z.TEST and Z.TEST array formulas, but for a straightforward Z score calculation, you can use the formula as described above. However, there isn't a specific built-in function named "Z SCORE" in Excel. Instead, you apply the Z score formula directly as shown.

Example

Suppose you have a set of exam scores and you want to calculate the Z score for a specific score to understand how it compares to the average, considering the standard deviation of the scores.

Score
80
70
85
90
75
  1. Calculate the mean: =AVERAGE(A1:A5) = 80
  2. Calculate the standard deviation: =STDEV.S(A1:A5) (assuming it's a sample) = 6.708203932
  3. To find the Z score for a score of 85:
    • =(85-80)/6.708203932 = 0.745355992

This Z score of approximately 0.75 means that the score of 85 is 0.75 standard deviations above the mean.

Embedding Images

Calculating Z Score in Excel

Gallery of Z Score Calculations

Z Score Calculations Image Gallery

Z Score Formula
Excel Z Score Calculation
Standard Deviation Calculation
Mean Calculation
Statistical Analysis
Data Interpretation
Excel Formulas
Spreadsheet Analysis
Data Analysis Techniques
Statistics for Beginners

FAQs

What is the Z score used for?

+

The Z score is used to compare a data point to the average of a dataset, taking into account the variability of the dataset.

How do I calculate the Z score in Excel?

+

You can calculate the Z score in Excel using the formula Z = (X - μ) / σ, where X is the value, μ is the mean, and σ is the standard deviation.

What is the difference between sample and population standard deviation?

+

The sample standard deviation (STDEV.S) is used when your data is a sample of a larger population, while the population standard deviation (STDEV.P) is used when your data represents the entire population.

Final Thoughts

Calculating the Z score in Excel is a straightforward process that can enhance your data analysis capabilities. By understanding how to apply the Z score formula and interpret its results, you can gain deeper insights into your data and make more informed decisions. Whether you're working with statistical analysis, quality control, or simply looking to understand your data better, mastering the Z score calculation in Excel is a valuable skill.

Excel Statistics

We hope this guide has been helpful in your journey to calculate Z scores in Excel. Feel free to share your thoughts, ask questions, or provide feedback in the comments below. Your engagement is invaluable in helping us create more relevant and useful content for you and our community.