Intro
Calculating the Annual Percentage Rate (APR) is a crucial task in personal finance, as it helps individuals understand the true cost of borrowing money. With the help of Excel, calculating APR can be a straightforward process. In this article, we will delve into the world of APR calculations, exploring the importance of APR, its components, and how to calculate it using Excel.
The Annual Percentage Rate (APR) is the rate charged on a loan or credit product over a year, including fees and compound interest. It is a critical factor in determining the affordability of a loan or credit card. A higher APR means that the borrower will pay more in interest over the life of the loan. Therefore, understanding how to calculate APR is essential for making informed financial decisions.
The APR calculation involves several components, including the nominal interest rate, fees, and compounding frequency. The nominal interest rate is the rate charged on the loan or credit product, while fees include any charges associated with the loan, such as origination fees or late payment fees. Compounding frequency refers to how often interest is calculated and added to the principal amount. In Excel, we can use formulas to calculate APR, taking into account these components.
Understanding APR Components

To calculate APR, we need to understand the components involved. The nominal interest rate, fees, and compounding frequency are all crucial factors in determining the APR. In Excel, we can use the following formula to calculate APR: APR = (Nominal Interest Rate + Fees) / Principal Amount. However, this formula does not take into account compounding frequency, which can significantly impact the APR.
Calculating APR using Excel Formulas
In Excel, we can use the following formula to calculate APR: APR = (1 + (Nominal Interest Rate / Number of Compounding Periods))^Number of Compounding Periods - 1. This formula takes into account the nominal interest rate, compounding frequency, and fees. By using this formula, we can accurately calculate the APR for a loan or credit product.For example, let's say we have a loan with a nominal interest rate of 12%, a principal amount of $10,000, and a compounding frequency of monthly. Using the formula above, we can calculate the APR as follows: APR = (1 + (0.12 / 12))^12 - 1 = 12.68%. This means that the APR for this loan is 12.68%, which is higher than the nominal interest rate.
Using Excel Functions to Calculate APR
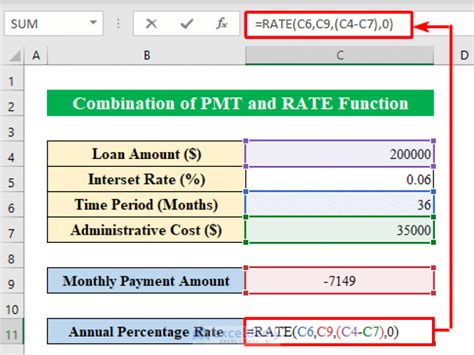
In addition to using formulas, we can also use Excel functions to calculate APR. The EFFECT function in Excel calculates the effective interest rate, which is equivalent to the APR. The syntax for the EFFECT function is: EFFECT(nominal_rate, npery), where nominal_rate is the nominal interest rate and npery is the number of compounding periods per year.
For example, using the same loan example above, we can calculate the APR using the EFFECT function as follows: EFFECT(0.12, 12) = 12.68%. This gives us the same result as the formula above.
Calculating APR for Credit Cards
Calculating APR for credit cards is slightly different than for loans. Credit cards often have a variable APR, which means that the APR can change over time. In Excel, we can use the following formula to calculate the APR for a credit card: APR = (1 + (Nominal Interest Rate / Number of Compounding Periods))^Number of Compounding Periods - 1.For example, let's say we have a credit card with a nominal interest rate of 18%, a principal amount of $5,000, and a compounding frequency of daily. Using the formula above, we can calculate the APR as follows: APR = (1 + (0.18 / 365))^365 - 1 = 19.56%. This means that the APR for this credit card is 19.56%, which is higher than the nominal interest rate.
APR Calculation Examples

To further illustrate the concept of APR calculation, let's consider a few examples. Suppose we have a loan with a nominal interest rate of 10%, a principal amount of $20,000, and a compounding frequency of quarterly. Using the formula above, we can calculate the APR as follows: APR = (1 + (0.10 / 4))^4 - 1 = 10.38%.
Another example is a credit card with a nominal interest rate of 20%, a principal amount of $3,000, and a compounding frequency of monthly. Using the formula above, we can calculate the APR as follows: APR = (1 + (0.20 / 12))^12 - 1 = 21.93%.
APR Calculation Tips and Tricks
When calculating APR, there are several tips and tricks to keep in mind. First, make sure to use the correct formula or function in Excel. Second, ensure that you have the correct inputs, such as the nominal interest rate, fees, and compounding frequency. Third, be aware of any assumptions or limitations of the formula or function used.Additionally, it's essential to consider the impact of fees on the APR calculation. Fees can significantly increase the APR, so it's crucial to include them in the calculation. Finally, be mindful of the compounding frequency, as it can also impact the APR calculation.
Common APR Calculation Mistakes

When calculating APR, there are several common mistakes to avoid. One of the most common mistakes is using the wrong formula or function in Excel. Another mistake is failing to include fees in the calculation. Additionally, not considering the compounding frequency can lead to inaccurate APR calculations.
To avoid these mistakes, it's essential to double-check your inputs and ensure that you are using the correct formula or function. Additionally, be aware of any assumptions or limitations of the formula or function used.
APR Calculation Best Practices
To ensure accurate APR calculations, there are several best practices to follow. First, use the correct formula or function in Excel. Second, ensure that you have the correct inputs, such as the nominal interest rate, fees, and compounding frequency. Third, be aware of any assumptions or limitations of the formula or function used.Additionally, consider using a spreadsheet template to calculate APR, as it can help simplify the process and reduce errors. Finally, always double-check your calculations to ensure accuracy.
Conclusion and Next Steps

In conclusion, calculating APR is a crucial task in personal finance, and Excel can be a powerful tool in this process. By understanding the components of APR, using the correct formulas or functions, and avoiding common mistakes, individuals can make informed financial decisions.
Next steps include applying the knowledge gained from this article to real-world scenarios, such as calculating APR for loans or credit cards. Additionally, individuals can explore other Excel functions and formulas to further enhance their financial analysis skills.
Gallery of APR Calculation Examples
APR Calculation Examples


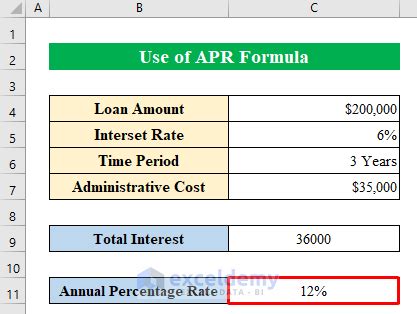



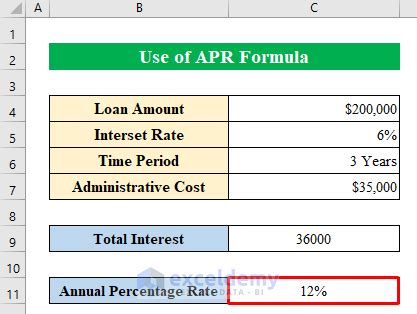



What is APR and why is it important?
+APR stands for Annual Percentage Rate, which is the rate charged on a loan or credit product over a year, including fees and compound interest. It's essential to understand APR because it helps individuals make informed financial decisions and avoid costly borrowing mistakes.
How do I calculate APR using Excel?
+To calculate APR using Excel, you can use the formula: APR = (1 + (Nominal Interest Rate / Number of Compounding Periods))^Number of Compounding Periods - 1. Alternatively, you can use the EFFECT function in Excel, which calculates the effective interest rate, equivalent to the APR.
What are the common mistakes to avoid when calculating APR?
+Common mistakes to avoid when calculating APR include using the wrong formula or function in Excel, failing to include fees in the calculation, and not considering the compounding frequency. To avoid these mistakes, double-check your inputs and ensure you are using the correct formula or function.
We hope this article has provided you with a comprehensive understanding of APR calculation using Excel. If you have any further questions or would like to share your experiences with APR calculation, please don't hesitate to comment below. Additionally, feel free to share this article with others who may benefit from this information. By working together, we can make informed financial decisions and achieve our financial goals.