Intro
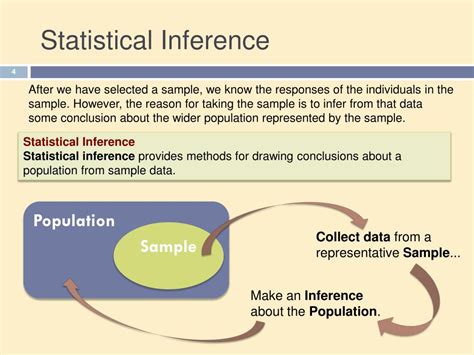
The concept of a confidence interval is crucial in statistics, providing a range of values within which a population parameter is likely to lie. It's a measure of the reliability of an estimate, and Excel, being a powerful tool for data analysis, offers various ways to visualize and calculate confidence intervals. In this article, we'll delve into how to create a confidence interval Excel graph, exploring its importance, the steps to create it, and interpreting the results.
Creating a confidence interval in Excel can significantly enhance your data analysis by giving you a clearer picture of the variability in your estimates. This is particularly useful in research, business, and social sciences, where understanding the margin of error in estimates is vital for making informed decisions. The confidence interval Excel graph serves as a visual representation, making it easier to understand complex statistical concepts at a glance.
To begin with, let's consider why confidence intervals are important. They offer a way to quantify the amount of uncertainty associated with a sample estimate, providing a range of values that is likely to include the true population parameter. This is crucial because sample estimates can vary from one sample to another, and confidence intervals give us a sense of how much the estimate might vary.
Understanding Confidence Intervals
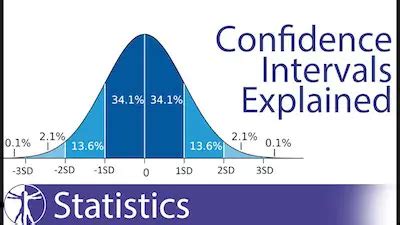
Before we dive into creating a confidence interval Excel graph, it's essential to understand the basics. A confidence interval is constructed from a sample of data and is used to estimate the population parameter. The width of the interval gives an indication of the precision of the estimate. Wider intervals indicate less precision, while narrower intervals suggest more precision.
Calculating Confidence Intervals in Excel
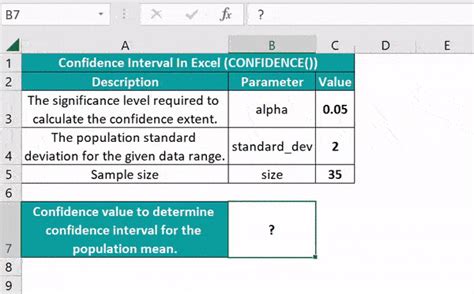
Excel provides several functions to calculate confidence intervals, such as the CONFIDENCE function for specific distributions. However, for more general cases, especially when dealing with large datasets, using the STDEV function to calculate the standard deviation of the sample and then applying the formula for the confidence interval can be more straightforward.
The formula for a confidence interval is given by: Sample Mean ± (Z-score * (Standard Deviation / sqrt(Sample Size))). Here, the Z-score corresponds to the desired confidence level, which can be looked up in a standard normal distribution table or calculated directly in Excel.
Creating a Confidence Interval Excel Graph
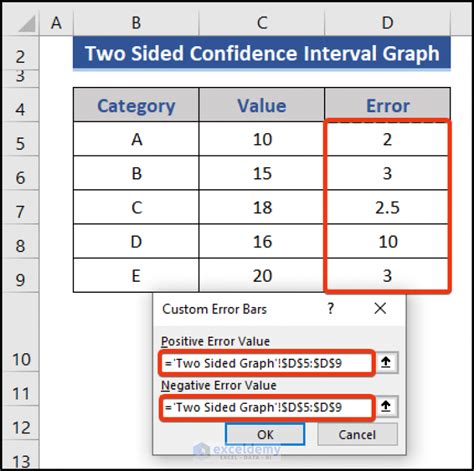
To create a confidence interval graph in Excel, follow these steps:
- Calculate the Sample Mean and Standard Deviation: Use the
AVERAGEandSTDEVfunctions to find these values. - Determine the Z-score: Based on your desired confidence level (e.g., 95%), find the corresponding Z-score.
- Calculate the Margin of Error: Use the formula Margin of Error = Z-score * (Standard Deviation / sqrt(Sample Size)).
- Find the Confidence Interval: Add and subtract the margin of error from the sample mean to get the upper and lower bounds of the interval.
- Plot the Data: Use Excel's charting tools to create a graph. A simple line chart or a bar chart can be effective for displaying the mean and the confidence interval.
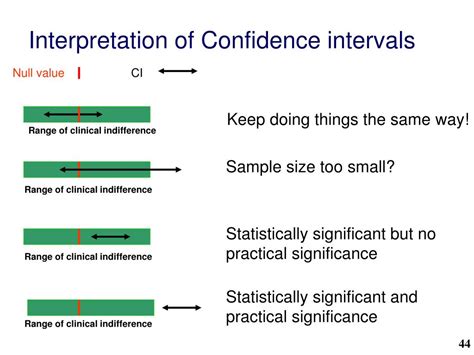
Interpreting the Confidence Interval Graph
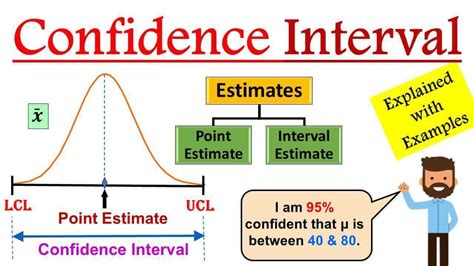
Interpreting the confidence interval graph involves understanding what the graph represents. The interval itself gives a range within which the true population parameter is likely to lie. If the interval is wide, it indicates less precision in the estimate, suggesting that more data might be needed to narrow down the interval.
Practical Applications

Confidence intervals have numerous practical applications across various fields. In business, they can be used to estimate market sizes or customer preferences. In medicine, confidence intervals are crucial for understanding the efficacy of treatments or the prevalence of diseases. They provide a statistical basis for decision-making, helping professionals to quantify uncertainty and make more informed choices.
Challenges and Limitations
While confidence intervals are powerful tools, they also come with challenges and limitations. The assumption of a normal distribution, the impact of sample size, and the choice of confidence level can all affect the interpretation of the results. Additionally, in real-world scenarios, data may not always meet the assumptions required for confidence interval calculations, necessitating the use of alternative methods or adjustments.
Advanced Topics and Future Directions

As statistical analysis evolves, so do the methods for constructing and interpreting confidence intervals. Advanced topics include the use of bootstrapping for non-parametric confidence intervals and the application of Bayesian methods for incorporating prior knowledge into interval estimates. These approaches offer more flexibility and can be particularly useful in complex data scenarios.
Conclusion and Recommendations

In conclusion, confidence intervals are a fundamental concept in statistical analysis, providing a quantitative measure of uncertainty. Excel, with its comprehensive set of statistical functions and graphing capabilities, is an ideal tool for calculating and visualizing confidence intervals. By understanding how to create and interpret confidence interval graphs in Excel, professionals can enhance their data analysis skills, making more accurate and informed decisions.
Confidence Interval Image Gallery





What is a confidence interval, and why is it important in statistics?
+A confidence interval provides a range of values within which a population parameter is likely to lie. It's a measure of the reliability of an estimate and is crucial for understanding the uncertainty associated with sample estimates.
How do I calculate a confidence interval in Excel?
+To calculate a confidence interval in Excel, you can use the CONFIDENCE function or calculate it manually using the formula: Sample Mean ± (Z-score * (Standard Deviation / sqrt(Sample Size))).
What are the practical applications of confidence intervals?
+Confidence intervals have numerous practical applications across various fields, including business, medicine, and social sciences. They are used to estimate population parameters, understand the efficacy of treatments, and make informed decisions.
We hope this comprehensive guide to confidence intervals and their visualization in Excel has been informative and helpful. Whether you're a student looking to understand statistical concepts better or a professional seeking to enhance your data analysis skills, mastering the art of creating and interpreting confidence interval graphs can significantly benefit your work. Feel free to share your thoughts, ask questions, or provide feedback in the comments section below.