Intro
Discover 3 ways to calculate matrix determinants, including expansion by minors, cofactor expansion, and rule of Sarrus, for linear algebra and math applications.
Determinants are a fundamental concept in linear algebra, and they play a crucial role in various mathematical and real-world applications. The determinant of a matrix can be calculated using different methods, each with its own advantages and disadvantages. In this article, we will explore three ways to calculate the determinant of a matrix, including the expansion by minors, the rule of Sarrus, and the LU decomposition method.
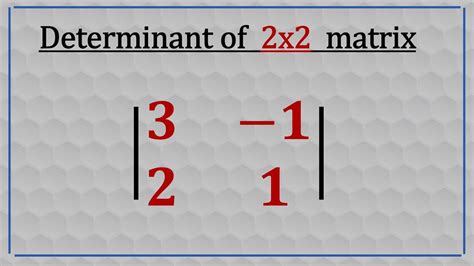
The determinant of a matrix is a scalar value that can be used to describe the scaling effect of the matrix on a region of space. It is a measure of the "volume" of the parallelepiped spanned by the column vectors of the matrix. The determinant is denoted as det(A) or |A| and is calculated using the elements of the matrix.
Introduction to Matrix Determinant

The determinant of a matrix has several important properties, including the fact that it is equal to zero if and only if the matrix is singular. This means that if the determinant of a matrix is zero, the matrix does not have an inverse. The determinant is also used in many applications, such as solving systems of linear equations, finding the inverse of a matrix, and calculating the eigenvalues and eigenvectors of a matrix.
Expansion by Minors Method

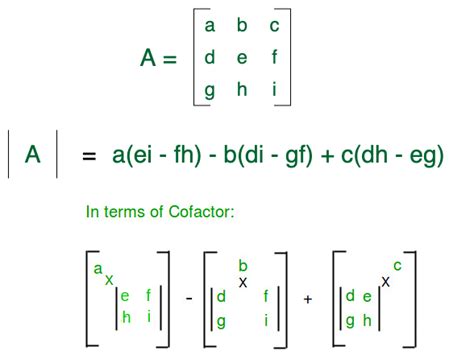
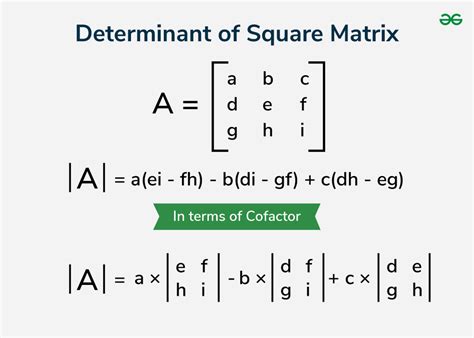
The expansion by minors method is a popular method for calculating the determinant of a matrix. This method involves expanding the determinant along a row or column of the matrix, using the minors of the elements in that row or column. The minor of an element is the determinant of the submatrix formed by removing the row and column containing that element.
To calculate the determinant using the expansion by minors method, we first choose a row or column to expand along. We then calculate the minor of each element in that row or column and multiply it by the cofactor of the element. The cofactor of an element is the minor of the element multiplied by (-1)^(i+j), where i and j are the row and column indices of the element.
Steps to Calculate Determinant using Expansion by Minors
- Choose a row or column to expand along.
- Calculate the minor of each element in the chosen row or column.
- Calculate the cofactor of each element by multiplying the minor by (-1)^(i+j).
- Multiply each element in the chosen row or column by its cofactor.
- Sum the products of the elements and their cofactors.
Rule of Sarrus Method
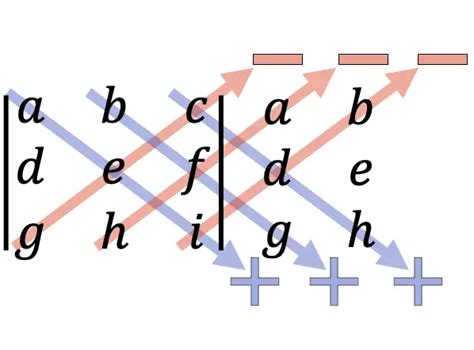
The rule of Sarrus is a method for calculating the determinant of a 3x3 matrix. This method involves duplicating the first two columns of the matrix and then calculating the sum of the products of the elements in the diagonals.
To calculate the determinant using the rule of Sarrus, we first duplicate the first two columns of the matrix. We then calculate the sum of the products of the elements in the diagonals, starting from the top-left element and moving down to the right. We also calculate the sum of the products of the elements in the diagonals, starting from the top-right element and moving down to the left.
Steps to Calculate Determinant using Rule of Sarrus
- Duplicate the first two columns of the matrix.
- Calculate the sum of the products of the elements in the diagonals, starting from the top-left element and moving down to the right.
- Calculate the sum of the products of the elements in the diagonals, starting from the top-right element and moving down to the left.
- Subtract the second sum from the first sum to get the determinant.
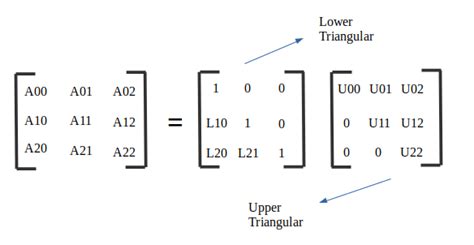
LU Decomposition Method

The LU decomposition method is a method for calculating the determinant of a matrix by decomposing it into a lower triangular matrix and an upper triangular matrix. This method involves using Gaussian elimination to transform the matrix into upper triangular form, and then calculating the determinant of the upper triangular matrix.
To calculate the determinant using the LU decomposition method, we first decompose the matrix into a lower triangular matrix and an upper triangular matrix. We then calculate the determinant of the upper triangular matrix by multiplying the elements on the diagonal.
Steps to Calculate Determinant using LU Decomposition
- Decompose the matrix into a lower triangular matrix and an upper triangular matrix.
- Calculate the determinant of the upper triangular matrix by multiplying the elements on the diagonal.
Matrix Determinant Image Gallery





What is the determinant of a matrix?
+The determinant of a matrix is a scalar value that can be used to describe the scaling effect of the matrix on a region of space.
How do I calculate the determinant of a 3x3 matrix?
+You can calculate the determinant of a 3x3 matrix using the rule of Sarrus or the expansion by minors method.
What is the LU decomposition method?
+The LU decomposition method is a method for calculating the determinant of a matrix by decomposing it into a lower triangular matrix and an upper triangular matrix.
In conclusion, calculating the determinant of a matrix is a crucial step in many mathematical and real-world applications. The expansion by minors, rule of Sarrus, and LU decomposition methods are three ways to calculate the determinant of a matrix, each with its own advantages and disadvantages. By understanding these methods and how to apply them, you can become proficient in calculating the determinant of a matrix and unlock the secrets of linear algebra. We invite you to share your thoughts and experiences with matrix determinants in the comments below, and don't forget to share this article with your friends and colleagues who may benefit from this information.