Enter Formula To Find Rank

Ranking systems are used in various fields, including education, sports, and information retrieval, to determine the position or standing of an item within a list or set. The formula to find the rank of an item depends on the specific ranking system being used. Here, we'll explore a general approach to ranking and provide a basic formula, along with explanations and examples to help illustrate the concept.

In many cases, ranking involves assigning a numerical score to each item based on certain criteria, and then sorting these scores in ascending or descending order to determine the rank. For instance, in a class, students might be ranked based on their grades, with the highest grade receiving the highest rank (often ranked as 1st) and the lowest grade receiving the lowest rank.

A basic formula to find the rank of an item, assuming you have a list of scores or values, could be considered as follows:

Arrange all scores in descending order (for a system where higher scores are better) or ascending order (for a system where lower scores are better).
Assign the rank based on the position in the sorted list, starting from 1 for the top score (in a descending order system) or the lowest score (in an ascending order system).

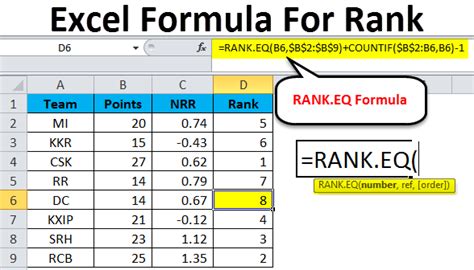
Mathematically, if you have a set of scores (S = {s_1, s_2,..., s_n}), and you want to find the rank (R_i) of a specific score (s_i), you first need to sort (S) in the appropriate order. Then, (R_i) is the position of (s_i) in the sorted set, with the first position being 1, the second being 2, and so on.

However, in more complex scenarios, such as in competitive ranking systems or when dealing with tied scores, the formula might need adjustments. For example, in a system that uses "standard competition ranking" (also known as "1224 ranking"), if two competitors are tied for the same rank, the next competitor ranks below both of them. In a "dense ranking" system, competitors with the same score receive the same rank, and the next rank is assigned without gaps.

To calculate ranks when there are ties, you might use a formula like this:

Identify all unique scores and their counts.
Assign ranks based on the unique scores, considering ties.
For each unique score, assign the same rank to all items with that score.
The next rank after a set of tied items is determined by the number of items in the tie plus one (for standard competition ranking) or simply the next rank without considering gaps (for dense ranking).

For instance, if you have scores 90, 85, 85, and 80, and you're using standard competition ranking:

The highest score (90) gets rank 1.
The tied scores (85) both get rank 2.
The next score (80) gets rank 4, because it ranks below both of the tied scores.

In a dense ranking system, the scores would be ranked as follows:

The highest score (90) gets rank 1.
The tied scores (85) both get rank 2.
The next score (80) gets rank 3, with no gap in ranking.

Given the complexity and variability of ranking systems, the specific formula or approach can vary significantly depending on the context and the rules of the ranking system being applied.

Understanding Ranking Systems

Ranking systems are essential in various aspects of life, from education and employment to sports and entertainment. They provide a way to compare and evaluate items or individuals based on specific criteria, helping to determine their standing or position within a group.

Types of Ranking Systems

There are several types of ranking systems, each with its own method of assigning ranks. Some common types include:

Standard Competition Ranking: This system assigns the same rank to tied items and then skips the next rank value. For example, if two items are tied for first place, the next item would be ranked third.
Dense Ranking: In this system, tied items receive the same rank, but the next item receives the next rank without skipping any rank values. Using the previous example, if two items are tied for first place, the next item would be ranked second.
Ordinal Ranking: This involves assigning a unique rank to each item based on its position in a sorted list. Ties are not allowed in ordinal ranking.
Fractional Ranking: This method assigns a fractional rank to items that are tied, based on the number of items tied and their position in the ranking.

Applications of Ranking Systems

Ranking systems have a wide range of applications across different fields. They are used in:

Education: To rank students based on their academic performance, helping to identify top performers and areas where students may need additional support.
Sports: To determine the standing of teams or individuals in a league or tournament, based on their win-loss records or points scored.
Employment: To evaluate job applicants or employees based on their qualifications, performance, or potential, aiding in hiring, promotion, or retention decisions.
Information Retrieval: In search engines, to rank web pages based on their relevance to a search query, ensuring that the most useful results appear at the top of the search results list.

Benefits and Challenges of Ranking Systems

Ranking systems offer several benefits, including facilitating comparison, encouraging competition, and providing a clear measure of performance or standing. However, they also present challenges, such as dealing with ties, ensuring fairness and transparency, and mitigating the potential for bias in the ranking criteria or process.

Implementing Ranking Systems Effectively

To implement a ranking system effectively, it's crucial to define clear criteria, ensure transparency in the ranking process, and regularly review and adjust the system as needed to maintain its relevance and fairness.

Effective Implementation of Ranking Systems

Future of Ranking Systems

As technology advances and data analysis becomes more sophisticated, ranking systems are likely to evolve, incorporating more nuanced and multidimensional criteria to provide a more accurate and comprehensive assessment of items or individuals being ranked.

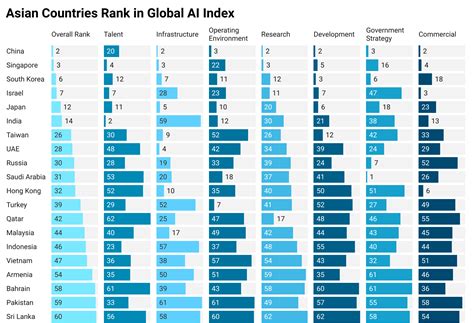
Ranking Systems Image Gallery

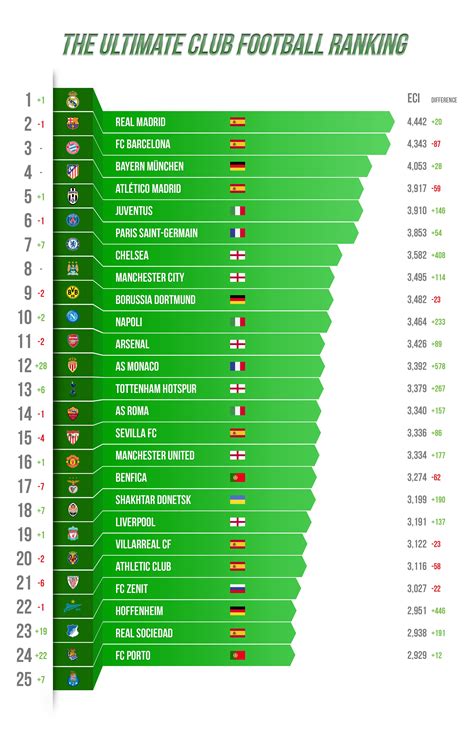
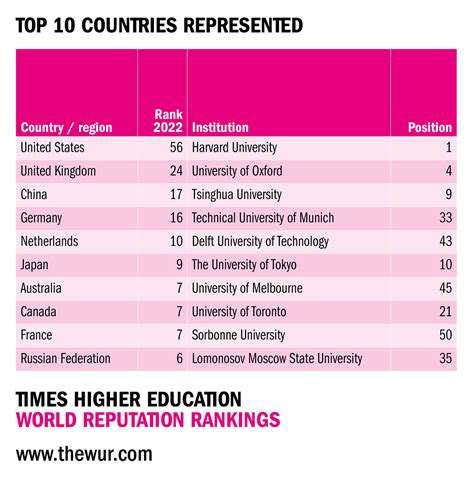
What is the purpose of a ranking system?

The primary purpose of a ranking system is to evaluate and compare items or individuals based on specific criteria, providing a clear and ordered list that reflects their relative standing or performance.

How do ranking systems handle ties?

Ranking systems handle ties in various ways, including standard competition ranking, where the next rank is skipped, and dense ranking, where the next rank is assigned without gaps. The method used depends on the specific system and its rules.

What are the benefits of using a ranking system?

The benefits of using a ranking system include facilitating comparison, encouraging competition, and providing a clear measure of performance or standing. Ranking systems can also help in decision-making processes by highlighting top performers or items that meet specific criteria.

We hope this comprehensive overview of ranking systems, including their types, applications, and challenges, has been informative and helpful. Whether you're looking to implement a ranking system in an educational setting, a sports league, or any other context, understanding the principles and methods behind ranking can help you make more informed decisions and evaluations. Feel free to share your thoughts or ask questions about ranking systems in the comments below.