Excel F-Test Two Sample Variances

Intro

The F-test is a statistical test used to determine whether two samples have the same variance. In Excel, the F-test can be used to compare the variances of two samples. This test is commonly used in statistical analysis to determine whether the variance of one sample is significantly different from the variance of another sample.

The F-test is a ratio of the variance of one sample to the variance of another sample. The test statistic is calculated as the ratio of the larger variance to the smaller variance. The F-test is sensitive to the assumption of normality, so it is essential to check for normality before performing the test.

The F-test can be used in a variety of situations, such as comparing the variability of two different manufacturing processes, comparing the variability of two different measurement instruments, or comparing the variability of two different populations. In each of these situations, the F-test can help determine whether the variability of one sample is significantly different from the variability of another sample.

To perform the F-test in Excel, you can use the F.TEST function or the Analysis ToolPak add-in. The F.TEST function takes two ranges of data as input and returns the p-value of the F-test. The Analysis ToolPak add-in provides a more comprehensive set of statistical tools, including the F-test.

How to Perform the F-Test in Excel

Excel F-Test

To perform the F-test in Excel, follow these steps:

  1. Enter the data for the two samples into two separate columns.
  2. Select the range of data for the first sample and go to the Formulas tab.
  3. Click on the Statistical button and select F-Test Two-Sample for Variances.
  4. Select the range of data for the second sample and click OK.
  5. The F-test statistic and p-value will be displayed in the output range.

Alternatively, you can use the F.TEST function to perform the F-test. The syntax for the F.TEST function is F.TEST(array1, array2), where array1 and array2 are the ranges of data for the two samples.

Interpreting the Results of the F-Test

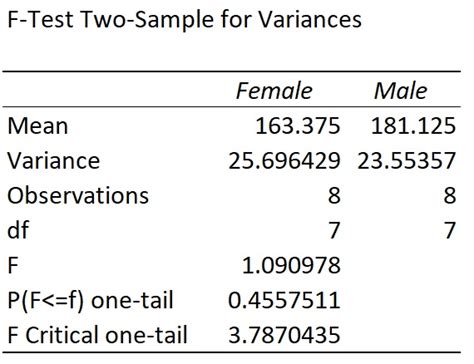
F-Test Results

The results of the F-test include the F-test statistic and the p-value. The F-test statistic is a ratio of the variance of one sample to the variance of another sample. The p-value is the probability of observing an F-test statistic as extreme or more extreme than the one observed, assuming that the variances of the two samples are equal.

If the p-value is less than a certain significance level (e.g. 0.05), you can reject the null hypothesis that the variances of the two samples are equal. This means that the variability of one sample is significantly different from the variability of another sample.

On the other hand, if the p-value is greater than the significance level, you cannot reject the null hypothesis that the variances of the two samples are equal. This means that the variability of one sample is not significantly different from the variability of another sample.

Assumptions of the F-Test

F-Test Assumptions

The F-test assumes that the data are normally distributed and that the samples are independent. If these assumptions are not met, the results of the F-test may not be reliable.

To check for normality, you can use the NORM.DIST function in Excel or the Normality Test in the Analysis ToolPak add-in. If the data are not normally distributed, you can transform the data to make it more normal.

To check for independence, you can use the CORREL function in Excel or the Correlation tool in the Analysis ToolPak add-in. If the samples are not independent, you may need to use a different statistical test.

Common Applications of the F-Test

F-Test Applications

The F-test has a wide range of applications in statistics and data analysis. Some common applications of the F-test include:

  • Comparing the variability of two different manufacturing processes
  • Comparing the variability of two different measurement instruments
  • Comparing the variability of two different populations
  • Determining whether a new manufacturing process is more variable than an existing process
  • Determining whether a new measurement instrument is more variable than an existing instrument

In each of these situations, the F-test can help determine whether the variability of one sample is significantly different from the variability of another sample.

Limitations of the F-Test

F-Test Limitations

The F-test has several limitations that should be considered when interpreting the results. Some limitations of the F-test include:

  • The F-test assumes that the data are normally distributed and that the samples are independent. If these assumptions are not met, the results of the F-test may not be reliable.
  • The F-test is sensitive to outliers and non-normality.
  • The F-test may not be suitable for small samples.
  • The F-test may not be suitable for comparing the variability of more than two samples.

In addition to these limitations, the F-test should be used in conjunction with other statistical tests and techniques to ensure that the results are reliable and accurate.

Alternatives to the F-Test

F-Test Alternatives

There are several alternatives to the F-test that can be used to compare the variability of two samples. Some alternatives to the F-test include:

  • The Levene test: This test is used to compare the variability of two or more samples and is more robust to non-normality than the F-test.
  • The Brown-Forsythe test: This test is used to compare the variability of two or more samples and is more robust to non-normality than the F-test.
  • The Bartlett test: This test is used to compare the variability of two or more samples and is more robust to non-normality than the F-test.

These alternatives to the F-test should be considered when the assumptions of the F-test are not met or when the results of the F-test are not reliable.

Excel F-Test Image Gallery

Excel F-Test
F-Test Results
F-Test Assumptions
F-Test Applications
F-Test Limitations
F-Test Alternatives
Excel Statistics
Statistical Analysis
Data Analysis
Excel Formulas

What is the F-test used for?

+

The F-test is used to compare the variances of two samples and determine whether they are significantly different.

What are the assumptions of the F-test?

+

The F-test assumes that the data are normally distributed and that the samples are independent.

What is the difference between the F-test and the Levene test?

+

The F-test is used to compare the variances of two samples, while the Levene test is used to compare the variances of two or more samples and is more robust to non-normality.

How do I perform the F-test in Excel?

+

To perform the F-test in Excel, you can use the `F.TEST` function or the `Analysis ToolPak` add-in.

What is the p-value of the F-test?

+

The p-value of the F-test is the probability of observing an F-test statistic as extreme or more extreme than the one observed, assuming that the variances of the two samples are equal.

In conclusion, the F-test is a powerful statistical tool used to compare the variances of two samples. By following the steps outlined in this article and using the F.TEST function or the Analysis ToolPak add-in in Excel, you can easily perform the F-test and determine whether the variability of one sample is significantly different from the variability of another sample. Remember to check the assumptions of the F-test and consider alternative tests if the assumptions are not met. With practice and experience, you can become proficient in using the F-test to analyze and interpret data in a variety of fields. We encourage you to share your thoughts and experiences with the F-test in the comments section below.