5 Ways Avoid Decimals

When dealing with numbers, decimals can sometimes be a nuisance, especially in certain mathematical operations or when presenting data in a specific format. There are several strategies to avoid decimals, each applicable in different contexts. Understanding these methods can help simplify calculations, improve data presentation, and enhance overall mathematical accuracy.

The importance of avoiding decimals lies in their potential to complicate calculations, especially when working with fractions or whole numbers. Decimals can lead to rounding errors, which might significantly affect the outcome of mathematical operations, particularly in fields like engineering, finance, and science. Moreover, in some educational contexts, students are encouraged to work with fractions to develop a deeper understanding of mathematical concepts before moving on to decimals.

Avoiding decimals can also make data more interpretable. For instance, in statistical analysis, presenting data in fractional form can sometimes offer a clearer insight into proportions and ratios than decimal representations. This is particularly true when communicating results to a general audience, as fractions can be more intuitive than decimals for certain types of data.

Furthermore, the ability to work without decimals enhances mathematical flexibility. It allows for a smoother transition between different mathematical operations and can simplify complex problems by reducing the need for conversion between decimal and fractional forms. This skill is invaluable in both academic and professional settings, where the ability to approach problems from multiple angles can be a significant advantage.

Avoiding Decimals in Mathematical Operations

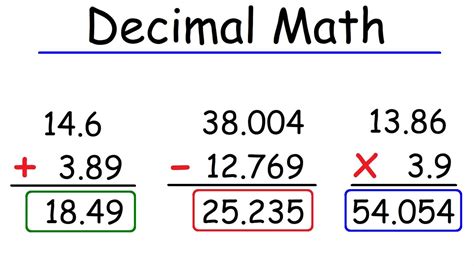
One of the primary ways to avoid decimals is by working with fractions instead of converting them into decimal form. This approach is particularly useful in algebra and geometry, where many problems can be solved using fractional coefficients and constants. By keeping numbers in fractional form, calculations can be performed without the introduction of decimals, thus avoiding potential rounding errors.

Another strategy involves using specific mathematical properties or identities that allow for the elimination of decimals. For example, in trigonometry, certain identities can be used to express trigonometric functions in terms of each other, potentially avoiding the need for decimal calculations. Similarly, in algebra, factoring and simplifying expressions can sometimes eliminate decimal coefficients.

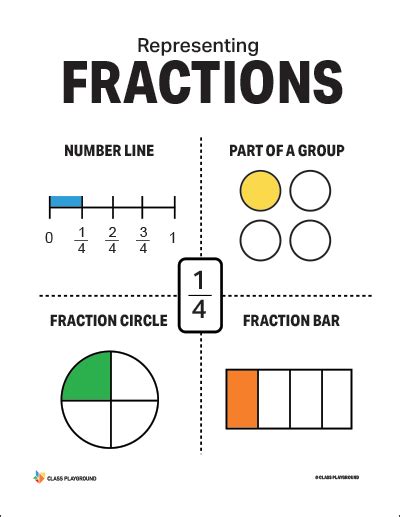
Using Fractions to Simplify Calculations

Fractions offer a powerful tool for avoiding decimals, as they can represent parts of a whole in a way that is often more intuitive and less prone to rounding errors than decimals. When performing calculations, especially multiplication and division, working with fractions can simplify the process by allowing for the cancellation of common factors, which reduces the complexity of the calculation and avoids the introduction of decimals.

Moreover, fractions can be easily converted into percentages or ratios, which are commonly used in statistical analysis and data presentation. This conversion can be particularly useful when comparing different datasets or when expressing changes over time, as it provides a clear and interpretable format for the data.

Benefits of Fractional Representation

The benefits of using fractions include:

• Accuracy: Fractions can represent numbers exactly, without the rounding errors associated with decimals.
• Simplicity: Fractions can simplify calculations by allowing for the cancellation of common factors.
• Intuitiveness: Fractions can provide a more intuitive understanding of proportions and ratios, especially when dealing with whole numbers.

Practical Applications of Avoiding Decimals

In practical terms, avoiding decimals can have significant implications in various fields. For instance, in engineering, precise calculations are crucial for the design and construction of structures, machines, and electronic devices. By working with fractions, engineers can ensure accuracy and avoid the potential for rounding errors that could compromise the safety and functionality of their designs.

Similarly, in finance, decimal places can significantly impact financial calculations, such as interest rates, investment returns, and currency exchange rates. Working with fractions can provide a more precise and transparent way of performing these calculations, reducing the risk of errors and ensuring fairness in financial transactions.

Fields Benefiting from Decimal Avoidance

Fields that benefit from avoiding decimals include:

• Engineering: For precise design and construction calculations.
• Finance: For accurate financial calculations and transactions.
• Science: For precise measurements and calculations in experiments and data analysis.

Technological Tools for Decimal Avoidance

With the advent of technology, various tools and software have been developed to assist in mathematical calculations, including those that help avoid decimals. Computer algebra systems (CAS), for example, can perform symbolic calculations, keeping numbers in fractional form and avoiding decimals unless specifically instructed to convert them.

Additionally, certain programming languages and mathematical software packages offer functions and libraries designed to work with fractions, providing precise control over numerical representations and calculations. These tools can be invaluable in both educational and professional settings, facilitating complex calculations and ensuring accuracy.

Features of Mathematical Software

Key features of mathematical software for decimal avoidance include:

• Symbolic Calculation: Performing calculations with symbols rather than numbers.
• Fractional Arithmetic: Supporting calculations with fractions.
• Precision Control: Allowing users to control the precision of calculations.

Conclusion and Future Directions

In conclusion, avoiding decimals in mathematical operations and data presentation offers several benefits, including enhanced accuracy, simplicity, and intuitiveness. By leveraging fractions, mathematical properties, and technological tools, individuals can simplify calculations, improve data interpretation, and reduce the risk of rounding errors.

As technology continues to evolve, we can expect to see further developments in tools and software designed to support decimal avoidance. These advancements will likely play a critical role in enhancing mathematical education, professional practices, and research methodologies, ultimately contributing to more precise and reliable outcomes across various fields.

Decimal Avoidance Image Gallery

What are the benefits of avoiding decimals in mathematical operations?

+

Avoiding decimals can enhance accuracy, simplify calculations, and provide a more intuitive understanding of proportions and ratios.

How can fractions be used to avoid decimals?

+

Fractions can represent parts of a whole exactly, without the need for decimals, and can be used to simplify calculations by canceling common factors.

What technological tools are available to assist in avoiding decimals?

+

Computer algebra systems, certain programming languages, and mathematical software packages offer functions and libraries designed to work with fractions and perform symbolic calculations, assisting in decimal avoidance.

We hope this article has provided valuable insights into the importance and methods of avoiding decimals in mathematical operations and data presentation. Whether you're a student looking to improve your mathematical skills, a professional seeking to enhance your calculation accuracy, or simply someone interested in the nuances of numerical representation, the strategies outlined here can offer significant benefits. Feel free to share your thoughts, experiences, or questions regarding decimal avoidance in the comments below, and don't hesitate to share this article with others who might find it useful.