Calculate Weighted Variance In Excel

Calculating weighted variance in Excel is a statistical process that takes into account the varying importance or weights of different data points. Unlike the standard variance calculation, which treats all data points equally, weighted variance allows for a more nuanced analysis by emphasizing certain data points over others. This can be particularly useful in scenarios where some observations have a greater impact on the overall outcome than others.

The concept of weighted variance is essential in many fields, including finance, engineering, and social sciences, where the importance of data points can vary significantly. For instance, in investment portfolios, different assets may have varying weights based on their proportion of the total portfolio, and calculating the weighted variance of returns can provide a more accurate picture of the portfolio's risk.

To calculate weighted variance in Excel, you can follow these steps, which involve using the formulas for weighted mean and weighted variance.

Understanding Weighted Mean and Variance

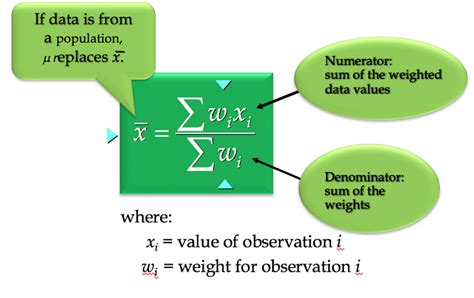
Before diving into the Excel implementation, it's crucial to understand the formulas for weighted mean and weighted variance. The weighted mean is calculated as the sum of the product of each data point and its weight, divided by the sum of all weights. The weighted variance is calculated using the formula:

[ \sigma^2 = \frac{\sum_{i=1}^{n} w_i (x_i - \mu)^2}{\sum_{i=1}^{n} w_i} ]

where:

• (x_i) is the (i)th data point,
• (w_i) is the weight of the (i)th data point,
• (\mu) is the weighted mean,
• (n) is the number of data points.

Implementing in Excel

To implement this calculation in Excel, follow these steps:

1. Prepare Your Data: Set up your data in two columns, one for the data points ((x_i)) and one for their corresponding weights ((w_i)).

2. Calculate Weighted Mean: Use the formula for weighted mean, which in Excel can be implemented using the SUMPRODUCT and SUM functions. Assuming your data is in column A and weights in column B, starting from row 1, the weighted mean formula would look something like this:

   =SUMPRODUCT(A1:A10, B1:B10) / SUM(B1:B10)
   

   Replace A1:A10 with your data range and B1:B10 with your weight range.

3. Calculate Weighted Variance: With the weighted mean calculated, you can proceed to calculate the weighted variance. This involves calculating the squared differences from the mean for each data point, multiplying by the weights, summing these, and then dividing by the sum of the weights. The formula for this, assuming the weighted mean is in cell C1, would be:

   =SUMPRODUCT(B1:B10, (A1:A10-C1)^2) / SUM(B1:B10)
   

   Again, adjust the ranges A1:A10 and B1:B10 according to your data.

Visualizing the Process

For better understanding, let's visualize the steps with an example:

Suppose we have the following data points and their respective weights:

Data Point	Weight
10	2
20	3
30	1

Step 1: Calculate Weighted Mean

Using the formula for weighted mean:

Weighted Mean = (10*2 + 20*3 + 30*1) / (2 + 3 + 1)
               = (20 + 60 + 30) / 6
               = 110 / 6
               = 18.33

Step 2: Calculate Weighted Variance

First, calculate the squared differences from the mean for each data point, then multiply by the weights, and sum these values.

Data Point	Weight	Difference from Mean	Squared Difference	Weighted Squared Difference
10	2	10 - 18.33 = -8.33	(-8.33)^2 = 69.39	69.39 * 2 = 138.78
20	3	20 - 18.33 = 1.67	(1.67)^2 = 2.79	2.79 * 3 = 8.37
30	1	30 - 18.33 = 11.67	(11.67)^2 = 136.19	136.19 * 1 = 136.19

Sum of weighted squared differences = 138.78 + 8.37 + 136.19 = 283.34

Sum of weights = 2 + 3 + 1 = 6

Weighted Variance = 283.34 / 6 = 47.22

Embedding Images

Practical Applications

• Portfolio Risk Assessment: In finance, calculating the weighted variance of a portfolio's assets helps in understanding the overall risk, where weights are based on the proportion of each asset in the portfolio.
• Quality Control: In manufacturing, weighted variance can be used to assess the quality of products, where certain defects may be weighted more heavily than others based on their impact on the final product.

Gallery of Weighted Variance Calculations

Weighted Variance Calculation Gallery

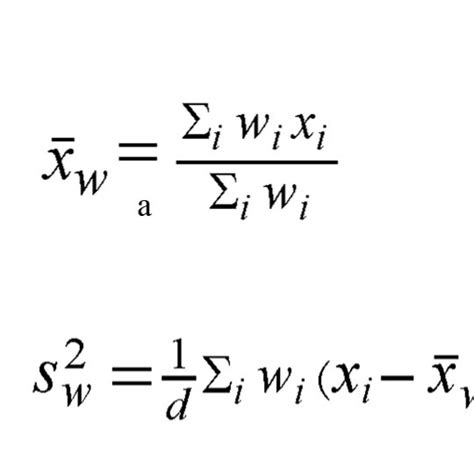
FAQs

What is weighted variance, and why is it important?

+

Weighted variance is a measure of dispersion that takes into account the varying importance of different data points. It's crucial in statistical analysis, especially in scenarios where some observations have a greater impact than others.

How do you calculate weighted variance in Excel?

+

To calculate weighted variance in Excel, first, calculate the weighted mean using the SUMPRODUCT and SUM functions. Then, use the weighted mean to calculate the weighted variance with the formula that involves the sum of the product of weights and squared differences from the mean, divided by the sum of weights.

What are some practical applications of weighted variance?

+

Weighted variance has practical applications in portfolio risk assessment, quality control, and any scenario where the importance of data points varies. It helps in understanding the dispersion of data points that have different weights or importance.

Final Thoughts

Calculating weighted variance is a powerful tool in statistical analysis, allowing for a more nuanced understanding of data dispersion when not all data points are equally important. By following the steps outlined and understanding the practical applications, individuals can leverage weighted variance to make more informed decisions in various fields. Whether it's assessing portfolio risk, evaluating quality control measures, or analyzing data with varying importance, weighted variance provides a valuable insight into the characteristics of the data.

We invite you to share your thoughts and experiences with calculating weighted variance, especially in how it has helped in your data analysis or decision-making processes. Your insights can be invaluable to others looking to apply weighted variance in their work or studies. Feel free to comment below or share this article with others who might benefit from understanding the concept and application of weighted variance.