Intro
The concept of computing years is crucial in various fields, including finance, technology, and environmental science. Understanding how to calculate years can help individuals and organizations make informed decisions about investments, project timelines, and resource allocation. In this article, we will explore five ways to compute years, highlighting their applications, benefits, and limitations.
Computing years is essential in finance, where it is used to calculate interest rates, investment returns, and loan repayment periods. It is also critical in technology, where it helps estimate the lifespan of equipment, software, and hardware. Moreover, computing years is vital in environmental science, where it is used to predict climate change, track population growth, and estimate the impact of human activities on the environment.
The importance of computing years cannot be overstated. It helps individuals and organizations plan for the future, make informed decisions, and avoid potential pitfalls. By understanding how to compute years, individuals can better manage their finances, make smart investment decisions, and achieve their long-term goals. Organizations can also use computing years to optimize their operations, reduce costs, and improve their overall performance.
Introduction to Computing Years

Computing years involves calculating the time it takes for a quantity to change or grow at a specific rate. It can be used to estimate the future value of an investment, the payoff period of a loan, or the lifespan of a product. There are various methods for computing years, each with its strengths and weaknesses. In this article, we will explore five common methods, including the rule of 72, the rule of 115, the present value formula, the future value formula, and the amortization schedule.
The Rule of 72

The rule of 72 is a simple and effective method for computing years. It estimates the number of years it takes for an investment to double in value, based on the interest rate. The formula is: years = 72 / interest rate. For example, if the interest rate is 8%, it will take approximately 9 years for the investment to double in value (72 / 8 = 9). This method is useful for estimating the growth rate of investments and comparing different investment options.
Benefits and Limitations of the Rule of 72
The rule of 72 is a useful tool for estimating the growth rate of investments. It is simple, easy to use, and provides a quick estimate of the time it takes for an investment to double in value. However, it has some limitations. It assumes a constant interest rate, which may not be the case in reality. It also does not take into account compounding interest, which can significantly impact the growth rate of an investment.
The Rule of 115

The rule of 115 is similar to the rule of 72, but it estimates the number of years it takes for an investment to triple in value. The formula is: years = 115 / interest rate. For example, if the interest rate is 8%, it will take approximately 14.4 years for the investment to triple in value (115 / 8 = 14.4). This method is useful for estimating the growth rate of investments and comparing different investment options.
Benefits and Limitations of the Rule of 115
The rule of 115 is a useful tool for estimating the growth rate of investments. It is simple, easy to use, and provides a quick estimate of the time it takes for an investment to triple in value. However, it has some limitations. It assumes a constant interest rate, which may not be the case in reality. It also does not take into account compounding interest, which can significantly impact the growth rate of an investment.
The Present Value Formula

The present value formula is a more complex method for computing years. It estimates the present value of a future cash flow, based on the interest rate and the time period. The formula is: present value = future value / (1 + interest rate)^years. For example, if the future value is $100, the interest rate is 8%, and the time period is 5 years, the present value would be approximately $68.44 ($100 / (1 + 0.08)^5).
Benefits and Limitations of the Present Value Formula
The present value formula is a useful tool for estimating the present value of future cash flows. It takes into account the interest rate and the time period, providing a more accurate estimate of the present value. However, it has some limitations. It assumes a constant interest rate, which may not be the case in reality. It also requires a detailed understanding of the formula and its application.
The Future Value Formula

The future value formula is similar to the present value formula, but it estimates the future value of a present cash flow. The formula is: future value = present value x (1 + interest rate)^years. For example, if the present value is $100, the interest rate is 8%, and the time period is 5 years, the future value would be approximately $146.93 ($100 x (1 + 0.08)^5).
Benefits and Limitations of the Future Value Formula
The future value formula is a useful tool for estimating the future value of present cash flows. It takes into account the interest rate and the time period, providing a more accurate estimate of the future value. However, it has some limitations. It assumes a constant interest rate, which may not be the case in reality. It also requires a detailed understanding of the formula and its application.
The Amortization Schedule
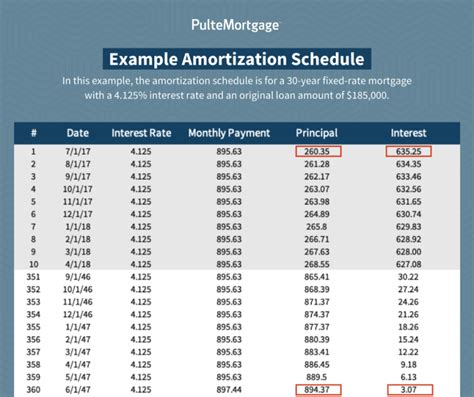
The amortization schedule is a method for computing years that is used to estimate the payoff period of a loan. It takes into account the loan amount, interest rate, and monthly payment, providing a detailed schedule of the loan payments and the outstanding balance. For example, if the loan amount is $100,000, the interest rate is 8%, and the monthly payment is $1,000, the amortization schedule would show the loan payments and the outstanding balance over the life of the loan.
Benefits and Limitations of the Amortization Schedule
The amortization schedule is a useful tool for estimating the payoff period of a loan. It provides a detailed schedule of the loan payments and the outstanding balance, helping individuals and organizations plan for the future. However, it has some limitations. It assumes a constant interest rate, which may not be the case in reality. It also requires a detailed understanding of the formula and its application.
Computing Years Image Gallery






What is computing years?
+Computing years involves calculating the time it takes for a quantity to change or grow at a specific rate.
What are the different methods for computing years?
+There are several methods for computing years, including the rule of 72, the rule of 115, the present value formula, the future value formula, and the amortization schedule.
What is the rule of 72?
+The rule of 72 is a simple and effective method for computing years. It estimates the number of years it takes for an investment to double in value, based on the interest rate.
What is the present value formula?
+The present value formula is a more complex method for computing years. It estimates the present value of a future cash flow, based on the interest rate and the time period.
What is the amortization schedule?
+The amortization schedule is a method for computing years that is used to estimate the payoff period of a loan. It takes into account the loan amount, interest rate, and monthly payment, providing a detailed schedule of the loan payments and the outstanding balance.
In conclusion, computing years is a crucial concept in various fields, including finance, technology, and environmental science. By understanding the different methods for computing years, individuals and organizations can make informed decisions about investments, project timelines, and resource allocation. We hope this article has provided you with a comprehensive understanding of computing years and its applications. If you have any questions or comments, please feel free to share them below. Additionally, if you found this article helpful, please share it with others who may benefit from this information.