Intro
Learn how to perform a Chi Square test in Excel, including hypothesis testing, statistical analysis, and data interpretation, using chi-squared distribution and Excel formulas.
The Chi Square test is a statistical method used to determine whether there is a significant association between two categorical variables. In Excel, you can perform a Chi Square test using the Analysis ToolPak add-in or by using formulas and functions. The test is commonly used in various fields, including social sciences, medicine, and marketing research, to analyze and understand the relationships between different variables.
Performing a Chi Square test on Excel can be a bit complex, but with the right steps, you can easily analyze your data and draw meaningful conclusions. The test is particularly useful when working with categorical data, such as yes/no responses, categories, or rankings. By using the Chi Square test, you can determine whether the observed frequencies in your data are significantly different from the expected frequencies, and make informed decisions based on your findings.
The importance of the Chi Square test lies in its ability to help researchers and analysts identify patterns and relationships in their data. By using this test, you can gain a deeper understanding of your data and make more accurate predictions and decisions. In this article, we will guide you through the process of performing a Chi Square test on Excel, and provide you with the knowledge and skills needed to analyze and interpret your results.
What is the Chi Square Test?

χ2 = Σ [(observed frequency - expected frequency)^2 / expected frequency]
where χ2 is the Chi Square statistic, observed frequency is the actual frequency of each category, and expected frequency is the frequency that would be expected if there were no association between the variables.
How to Calculate the Expected Frequencies
To calculate the expected frequencies, you need to multiply the row total by the column total and divide by the grand total. For example, if you have a 2x2 contingency table with the following frequencies:| Yes | No | Total | |
|---|---|---|---|
| Male | 20 | 30 | 50 |
| Female | 30 | 20 | 50 |
| Total | 50 | 50 | 100 |
The expected frequency for the cell "Male" and "Yes" would be:
Expected frequency = (50 x 50) / 100 = 25
How to Perform a Chi Square Test on Excel
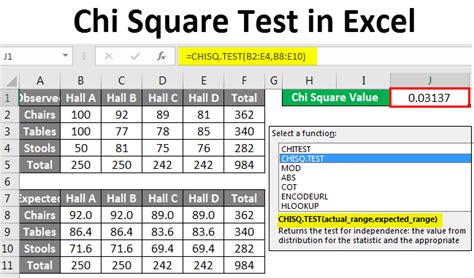
- Enter your data into a contingency table, with the categories for one variable in the rows and the categories for the other variable in the columns.
- Calculate the expected frequencies for each cell using the formula described above.
- Calculate the Chi Square statistic using the formula:
χ2 = Σ [(observed frequency - expected frequency)^2 / expected frequency]
- Determine the degrees of freedom for the test, which is (number of rows - 1) x (number of columns - 1).
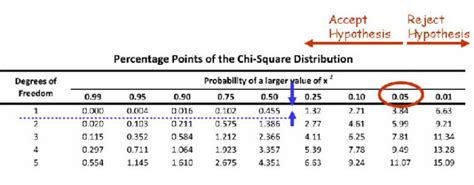
- Look up the critical value for the Chi Square distribution using a Chi Square table or calculator.
- Compare the calculated Chi Square statistic to the critical value. If the calculated statistic is greater than the critical value, you can reject the null hypothesis and conclude that there is a significant association between the variables.
Using the Analysis ToolPak Add-in
Alternatively, you can use the Analysis ToolPak add-in in Excel to perform a Chi Square test. To do this, follow these steps:- Go to the "Data" tab and click on "Data Analysis".
- Select "Chi-Square Test" from the list of available tests.
- Enter the range of cells that contains your data.
- Click "OK" to run the test.
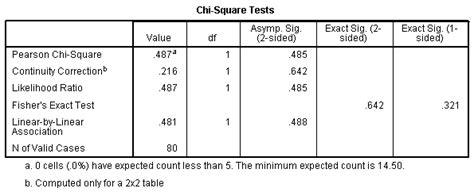
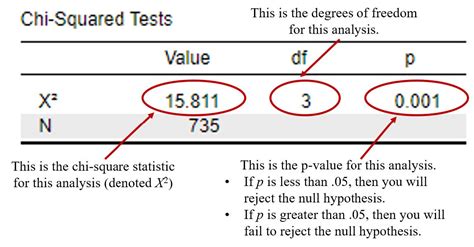
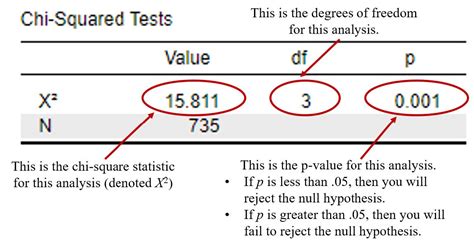
- The output will include the Chi Square statistic, the degrees of freedom, and the p-value.
Interpreting the Results
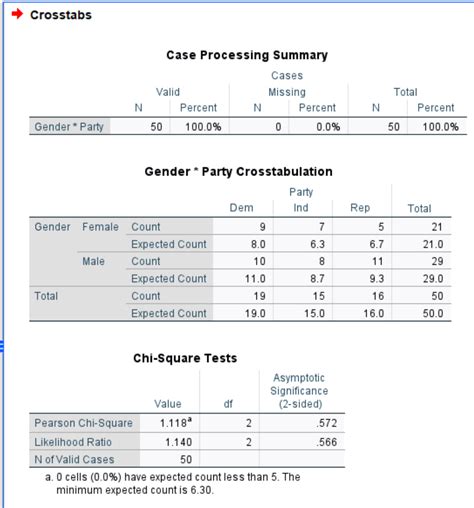
- The Chi Square statistic (χ2)
- The degrees of freedom (df)
- The p-value
The p-value represents the probability of obtaining the observed frequencies (or more extreme frequencies) assuming that there is no association between the variables. If the p-value is less than a certain significance level (usually 0.05), you can reject the null hypothesis and conclude that there is a significant association between the variables.
For example, if the p-value is 0.01, this means that there is only a 1% chance of obtaining the observed frequencies (or more extreme frequencies) assuming that there is no association between the variables. In this case, you can reject the null hypothesis and conclude that there is a significant association between the variables.
Common Mistakes to Avoid
When performing a Chi Square test, there are several common mistakes to avoid, including:- Failing to check the assumptions of the test, such as independence of observations and adequate sample size.
- Failing to calculate the expected frequencies correctly.
- Failing to determine the degrees of freedom correctly.
- Failing to look up the critical value for the Chi Square distribution correctly.
- Failing to interpret the results correctly, including failing to consider the p-value and the significance level.
By avoiding these common mistakes, you can ensure that your Chi Square test is performed correctly and that your results are valid and reliable.
Gallery of Chi Square Test Images
Chi Square Test Image Gallery




What is the purpose of the Chi Square test?
+The purpose of the Chi Square test is to determine whether there is a significant association between two categorical variables.
How do I calculate the expected frequencies for the Chi Square test?
+To calculate the expected frequencies, you need to multiply the row total by the column total and divide by the grand total.
What is the significance level for the Chi Square test?
+The significance level for the Chi Square test is usually 0.05, which means that if the p-value is less than 0.05, you can reject the null hypothesis and conclude that there is a significant association between the variables.
How do I interpret the results of the Chi Square test?
+The output of the Chi Square test will include the Chi Square statistic, the degrees of freedom, and the p-value. If the p-value is less than the significance level, you can reject the null hypothesis and conclude that there is a significant association between the variables.
What are some common mistakes to avoid when performing a Chi Square test?
+Some common mistakes to avoid when performing a Chi Square test include failing to check the assumptions of the test, failing to calculate the expected frequencies correctly, and failing to interpret the results correctly.
In final thoughts, performing a Chi Square test on Excel can be a bit complex, but with the right steps and knowledge, you can easily analyze your data and draw meaningful conclusions. By following the steps outlined in this article and avoiding common mistakes, you can ensure that your Chi Square test is performed correctly and that your results are valid and reliable. We encourage you to share your experiences and tips for performing a Chi Square test on Excel in the comments below, and to share this article with others who may be interested in learning more about this statistical method.