Intro
Calculate area under curves in Excel using integral functions, numerical methods, and graphing tools, with step-by-step guides and formulas for accurate results.
Calculating the area under a curve is a fundamental concept in mathematics and statistics, and it has numerous applications in various fields such as physics, engineering, economics, and computer science. In Excel, calculating the area under a curve can be achieved using several methods, including the use of formulas, charts, and add-ins. In this article, we will explore the different methods of calculating the area under a curve in Excel, along with their advantages and disadvantages.
The importance of calculating the area under a curve cannot be overstated. It is used to determine the definite integral of a function, which has numerous applications in physics, engineering, and economics. For instance, it can be used to calculate the area under a velocity-time graph to determine the distance traveled by an object. Similarly, it can be used to calculate the area under a probability density function to determine the probability of a random variable falling within a certain range.
Calculating the area under a curve can be challenging, especially when dealing with complex functions. However, with the use of Excel, this task can be simplified. Excel provides a range of tools and formulas that can be used to calculate the area under a curve, including the use of numerical integration methods such as the trapezoidal rule and Simpson's rule.
Introduction to Calculating Area Under A Curve
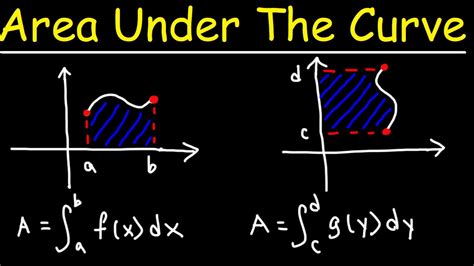
To calculate the area under a curve in Excel, we need to understand the concept of definite integrals. A definite integral is a mathematical operation that calculates the area under a curve between two points. It is denoted by the symbol ∫ and is calculated using the formula ∫f(x)dx, where f(x) is the function and dx is the infinitesimal change in x.
Methods of Calculating Area Under A Curve
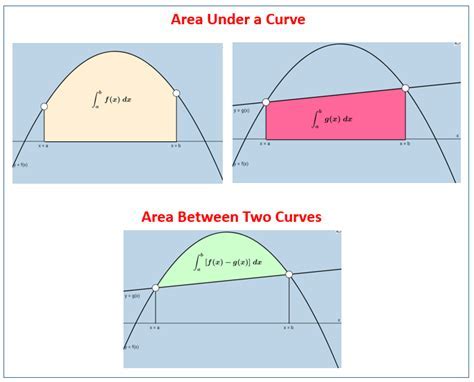
There are several methods of calculating the area under a curve in Excel, including:
- Using the
=INTfunction to calculate the definite integral of a function - Using the
=SUMfunction to calculate the area under a curve using the trapezoidal rule - Using the
=SUMfunction to calculate the area under a curve using Simpson's rule - Using charts to visualize the area under a curve
- Using add-ins such as the Analysis ToolPak to calculate the area under a curve
Each of these methods has its advantages and disadvantages, and the choice of method depends on the complexity of the function and the desired level of accuracy.
Using the =INT Function

The =INT function is used to calculate the definite integral of a function. It takes two arguments: the function and the upper limit of integration. For example, to calculate the definite integral of the function x^2 from 0 to 4, we can use the formula =INT(x^2,0,4).
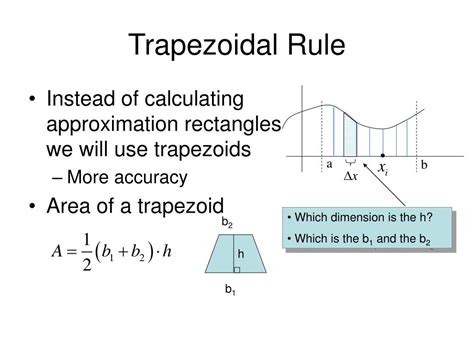
Using the =SUM Function with the Trapezoidal Rule

The trapezoidal rule is a numerical integration method that calculates the area under a curve by dividing the area into trapezoids and summing the areas of the trapezoids. To use the trapezoidal rule in Excel, we can use the =SUM function to calculate the sum of the areas of the trapezoids.
Using the =SUM Function with Simpson's Rule

Simpson's rule is another numerical integration method that calculates the area under a curve by dividing the area into parabolic segments and summing the areas of the parabolic segments. To use Simpson's rule in Excel, we can use the =SUM function to calculate the sum of the areas of the parabolic segments.
Advantages and Disadvantages of Each Method
Each of the methods of calculating the area under a curve in Excel has its advantages and disadvantages. The =INT function is easy to use but may not be accurate for complex functions. The trapezoidal rule and Simpson's rule are more accurate but require more complex formulas and may be time-consuming to set up.
Advantages of the =INT Function
The =INT function is easy to use and requires minimal setup. It is also relatively fast and can handle complex functions.
Disadvantages of the =INT Function
The =INT function may not be accurate for complex functions and may not be able to handle functions with multiple local maxima or minima.
Advantages of the Trapezoidal Rule
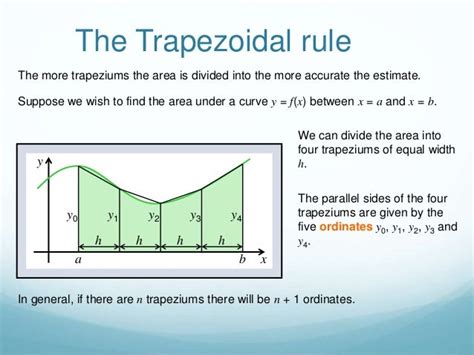
The trapezoidal rule is more accurate than the =INT function and can handle complex functions. It is also relatively easy to set up and use.
Disadvantages of the Trapezoidal Rule
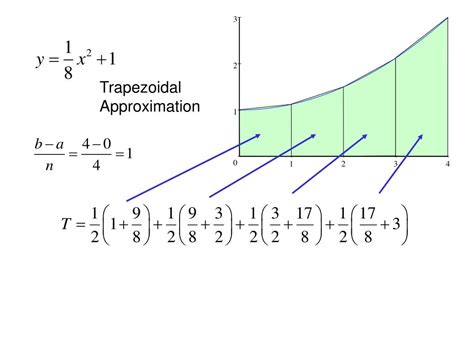
The trapezoidal rule requires more complex formulas and may be time-consuming to set up. It also may not be as accurate as Simpson's rule for very complex functions.
Advantages of Simpson's Rule

Simpson's rule is more accurate than the trapezoidal rule and can handle very complex functions. It is also relatively easy to set up and use.
Disadvantages of Simpson's Rule
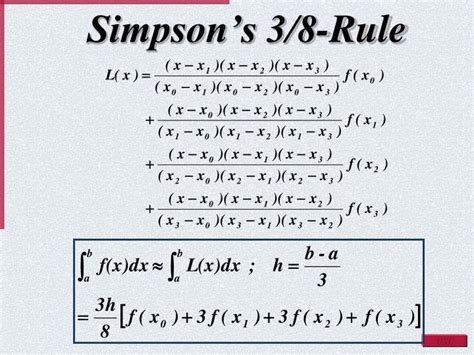
Simpson's rule requires more complex formulas and may be time-consuming to set up. It also may not be as fast as the =INT function or the trapezoidal rule.
Calculating Area Under Curve Image Gallery





What is the area under a curve?
+The area under a curve is the definite integral of a function, which represents the area between the curve and the x-axis.
How do I calculate the area under a curve in Excel?
+There are several methods to calculate the area under a curve in Excel, including using the `=INT` function, the trapezoidal rule, and Simpson's rule.
What is the difference between the trapezoidal rule and Simpson's rule?
+The trapezoidal rule and Simpson's rule are both numerical integration methods, but Simpson's rule is more accurate and can handle more complex functions.
Can I use Excel to calculate the area under a curve for any function?
+Yes, Excel can be used to calculate the area under a curve for any function, but the accuracy of the result may depend on the complexity of the function and the method used.
What are some common applications of calculating the area under a curve?
+Calculating the area under a curve has numerous applications in physics, engineering, economics, and computer science, including calculating distances, velocities, and probabilities.
In conclusion, calculating the area under a curve is an important concept in mathematics and statistics, and it has numerous applications in various fields. Excel provides several methods to calculate the area under a curve, including the use of formulas, charts, and add-ins. By understanding the different methods and their advantages and disadvantages, users can choose the best method for their specific needs and calculate the area under a curve with accuracy and precision. We encourage readers to share their experiences and tips on calculating the area under a curve in Excel, and to ask any questions they may have on this topic.