Intro
Learn to calculate area under curves in Excel using integrals, charts, and formulas, with tips on numerical integration and curve fitting for accurate results.
Calculating the area under a curve is a fundamental concept in mathematics and statistics, and it has numerous applications in various fields, including physics, engineering, economics, and finance. In Excel, calculating the area under a curve can be done using several methods, including numerical integration, approximation formulas, and built-in functions. In this article, we will explore the different methods for calculating the area under a curve in Excel, their advantages and limitations, and provide examples and illustrations to help readers understand the concepts.
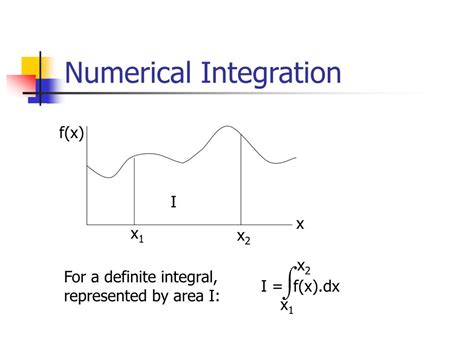
The area under a curve is a measure of the total amount of change or accumulation of a quantity over a given interval. It is commonly used to calculate the definite integral of a function, which represents the area between the curve and the x-axis. The area under a curve can be calculated using various methods, including the rectangle method, trapezoidal rule, and Simpson's rule. Each method has its own advantages and limitations, and the choice of method depends on the specific application and the desired level of accuracy.
Introduction to Numerical Integration in Excel
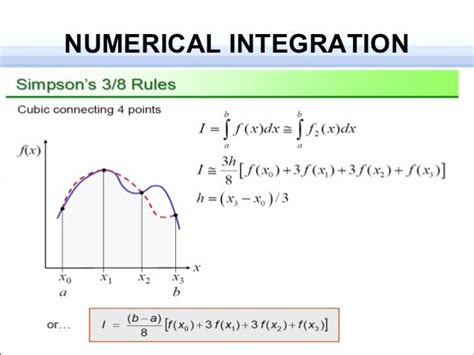
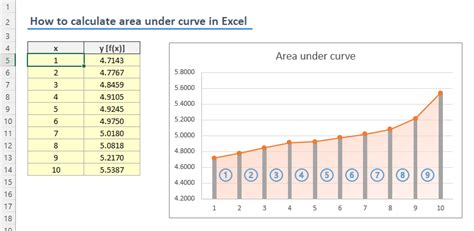
Numerical integration is a method for approximating the value of a definite integral using numerical techniques. In Excel, numerical integration can be performed using the SUM function, which calculates the sum of a series of values. The SUM function can be used to approximate the area under a curve by dividing the area into small rectangles and summing the areas of the rectangles. This method is simple and easy to implement, but it may not be accurate for curves with complex shapes or rapid changes.
Approximation Formulas for Calculating Area Under a Curve

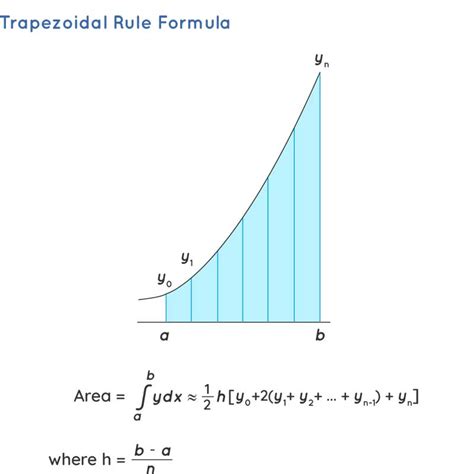
Approximation formulas are mathematical formulas that can be used to approximate the area under a curve. These formulas are based on the shape of the curve and the number of data points available. Some common approximation formulas include the trapezoidal rule, Simpson's rule, and the rectangle method. The trapezoidal rule approximates the area under a curve by dividing the area into trapezoids and summing the areas of the trapezoids. Simpson's rule approximates the area under a curve by dividing the area into parabolic segments and summing the areas of the segments.
Trapezoidal Rule
The trapezoidal rule is a simple and widely used method for approximating the area under a curve. The formula for the trapezoidal rule is:Area = (h/2) * (y0 + y1 + 2*y2 + 2*y3 +... + 2*yn-1 + yn)
where h is the width of each subinterval, and y0, y1, y2,..., yn are the function values at the subinterval points.
Simpson's Rule
Simpson's rule is a more accurate method for approximating the area under a curve. The formula for Simpson's rule is:Area = (h/3) * (y0 + 4*y1 + 2*y2 + 4*y3 +... + 2*yn-1 + yn)
where h is the width of each subinterval, and y0, y1, y2,..., yn are the function values at the subinterval points.
Using Built-in Functions in Excel to Calculate Area Under a Curve

Excel provides several built-in functions that can be used to calculate the area under a curve, including the INT function, SUM function, and LINEST function. The INT function calculates the definite integral of a function, while the SUM function calculates the sum of a series of values. The LINEST function calculates the linear regression of a set of data points.
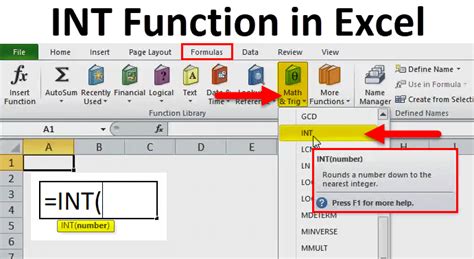
INT Function
The `INT` function calculates the definite integral of a function. The syntax for the `INT` function is:INT(x, y, lower_limit, upper_limit)
where x and y are the input arrays, lower_limit is the lower limit of integration, and upper_limit is the upper limit of integration.
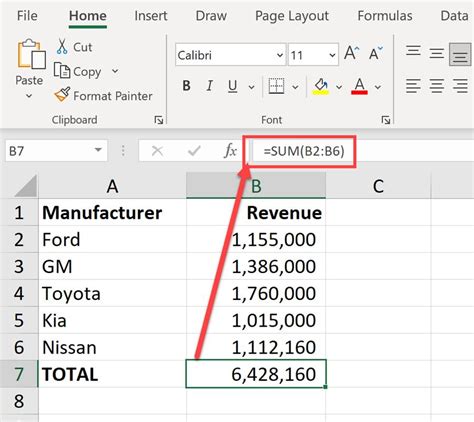
SUM Function
The `SUM` function calculates the sum of a series of values. The syntax for the `SUM` function is:SUM(range)
where range is the range of cells that contains the values to be summed.
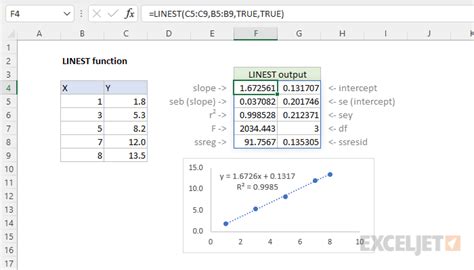
LINEST Function
The `LINEST` function calculates the linear regression of a set of data points. The syntax for the `LINEST` function is:LINEST(y, x, const)
where y is the dependent variable, x is the independent variable, and const is a logical value that specifies whether to force the intercept to be 0.
Practical Examples of Calculating Area Under a Curve in Excel
Calculating the area under a curve has numerous practical applications in various fields, including physics, engineering, economics, and finance. For example, in physics, the area under a curve can be used to calculate the work done by a force, while in economics, it can be used to calculate the total revenue or total cost of a firm.
Example 1: Calculating the Work Done by a Force
Suppose we have a force F(x) that varies with distance x, and we want to calculate the work done by the force in moving an object from x = 0 to x = 10. We can use the `INT` function to calculate the definite integral of the force function, which represents the work done by the force.Example 2: Calculating the Total Revenue of a Firm
Suppose we have a firm that produces a product with a demand function p(x) that varies with quantity x, and we want to calculate the total revenue of the firm. We can use the `SUM` function to calculate the sum of the revenue at each quantity level, which represents the total revenue of the firm.Gallery of Calculating Area Under a Curve
Calculating Area Under a Curve Image Gallery


Frequently Asked Questions
What is the area under a curve?
+The area under a curve is a measure of the total amount of change or accumulation of a quantity over a given interval.
How can I calculate the area under a curve in Excel?
+You can calculate the area under a curve in Excel using numerical integration, approximation formulas, or built-in functions such as the INT function, SUM function, and LINEST function.
What is the difference between the trapezoidal rule and Simpson's rule?
+The trapezoidal rule approximates the area under a curve by dividing the area into trapezoids, while Simpson's rule approximates the area under a curve by dividing the area into parabolic segments.
Can I use the INT function to calculate the area under a curve?
+Yes, you can use the INT function to calculate the definite integral of a function, which represents the area under a curve.
What are some practical applications of calculating the area under a curve?
+Calculating the area under a curve has numerous practical applications in various fields, including physics, engineering, economics, and finance, such as calculating the work done by a force, total revenue of a firm, and total cost of a firm.
In conclusion, calculating the area under a curve is a fundamental concept in mathematics and statistics, and it has numerous applications in various fields. Excel provides several methods for calculating the area under a curve, including numerical integration, approximation formulas, and built-in functions. By understanding these methods and their advantages and limitations, readers can apply them to solve real-world problems and make informed decisions. We invite readers to share their experiences and ask questions about calculating the area under a curve in Excel, and we hope that this article has provided a comprehensive and informative guide to this important topic.