Intro
Calculate distances with the Euclidean Distance Formula in Excel, using metrics like coordinates and dimensions to find proximity, similarity, and clustering, making data analysis and visualization easier with precise measurements.
The Euclidean distance formula is a fundamental concept in mathematics and statistics, used to calculate the distance between two points in a multi-dimensional space. In Excel, this formula can be implemented using various methods, making it a powerful tool for data analysis and visualization. In this article, we will delve into the world of Euclidean distance, exploring its importance, applications, and implementation in Excel.
The Euclidean distance formula is essential in various fields, including physics, engineering, computer science, and data analysis. It is used to calculate the straight-line distance between two points in a multi-dimensional space, which is crucial in understanding the relationships between data points. The formula is named after the ancient Greek mathematician Euclid, who first introduced the concept of distance in his book "Elements." The Euclidean distance formula is a simple yet powerful tool that has been widely used in various applications, from calculating distances between cities to analyzing gene expression data.
In data analysis, the Euclidean distance formula is used to calculate the similarity or dissimilarity between data points. It is a measure of how far apart two points are, which can be used to identify patterns, clusters, and relationships in the data. The formula is also used in machine learning algorithms, such as k-means clustering and k-nearest neighbors, to classify data points into different categories. The importance of the Euclidean distance formula cannot be overstated, as it provides a simple yet effective way to analyze and understand complex data.
What is Euclidean Distance Formula?
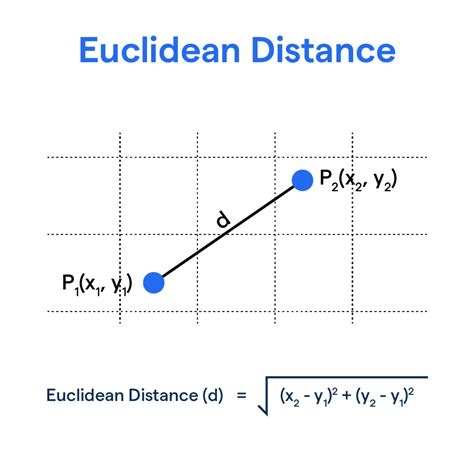
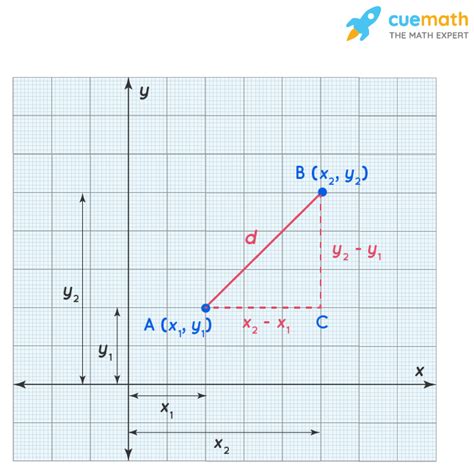
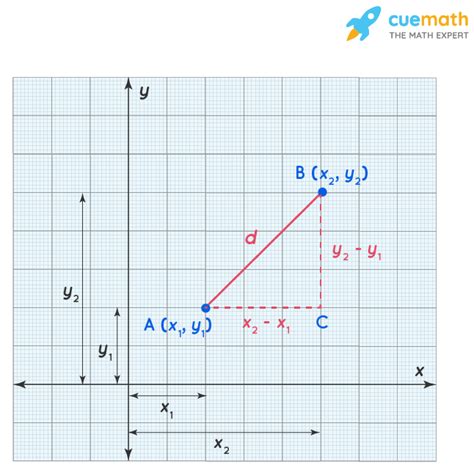
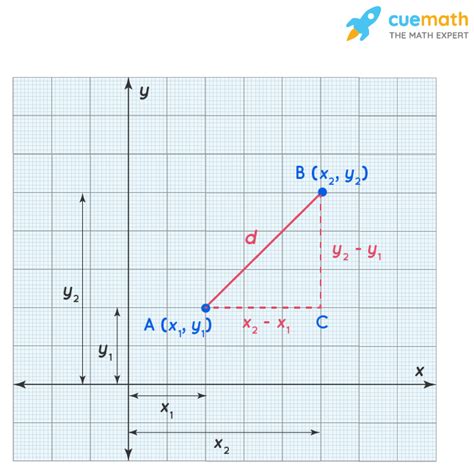
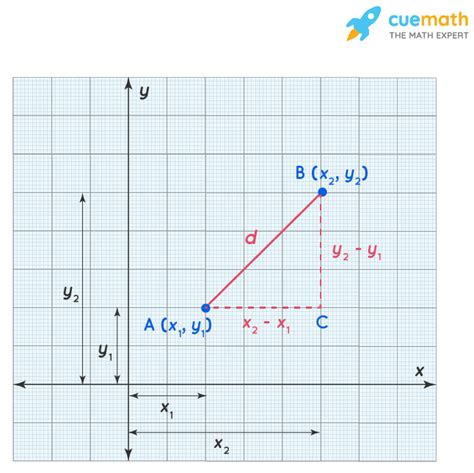
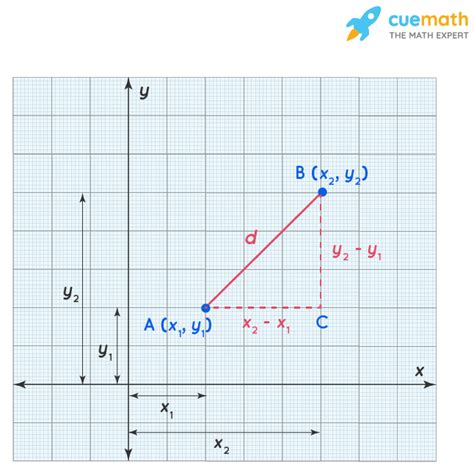
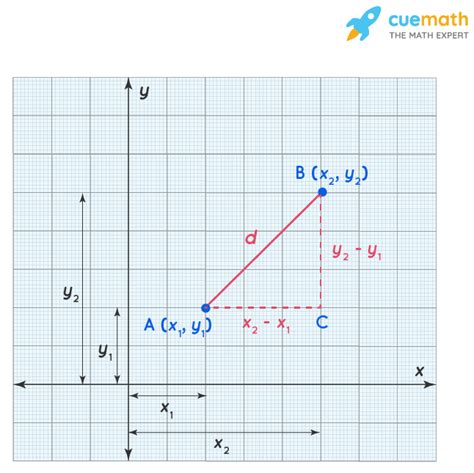
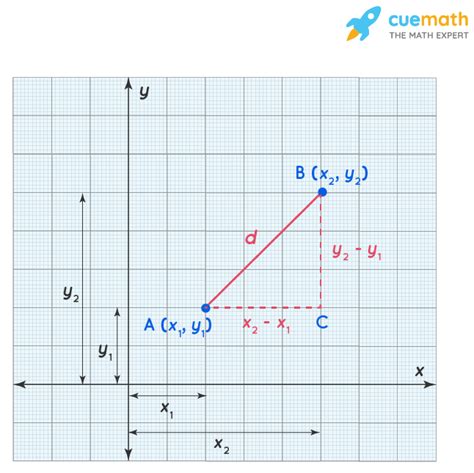
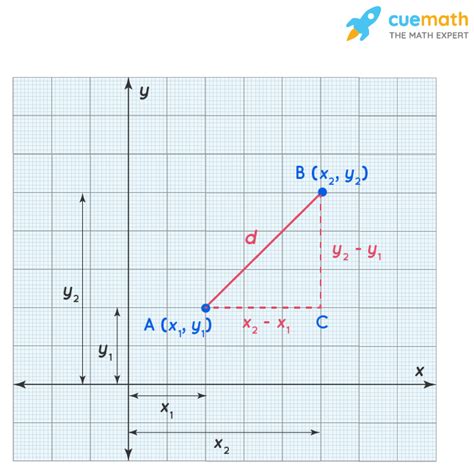
The Euclidean distance formula is a mathematical formula that calculates the distance between two points in a multi-dimensional space. The formula is based on the Pythagorean theorem, which states that the square of the length of the hypotenuse of a right triangle is equal to the sum of the squares of the lengths of the other two sides. The Euclidean distance formula is a direct application of this theorem, where the distance between two points is calculated as the square root of the sum of the squares of the differences between the corresponding coordinates.
The Euclidean distance formula can be expressed mathematically as:
d = √((x2 - x1)^2 + (y2 - y1)^2)
where d is the distance between the two points, (x1, y1) and (x2, y2) are the coordinates of the two points, and ^2 denotes the square of the difference.
How to Calculate Euclidean Distance in Excel

Calculating the Euclidean distance in Excel can be done using various methods, including using formulas, functions, and add-ins. One of the simplest ways to calculate the Euclidean distance is by using the formula:
=SQRT((x2-x1)^2+(y2-y1)^2)
where x1, y1, x2, and y2 are the coordinates of the two points.
Alternatively, you can use the Euclidean distance function in Excel, which is available in the Analysis ToolPak add-in. To use this function, follow these steps:
- Install the Analysis ToolPak add-in in Excel.
- Select the cell where you want to calculate the Euclidean distance.
- Type "=EUCLIDEAN(x1, y1, x2, y2)" and press Enter.
where x1, y1, x2, and y2 are the coordinates of the two points.
Example of Euclidean Distance Calculation in Excel
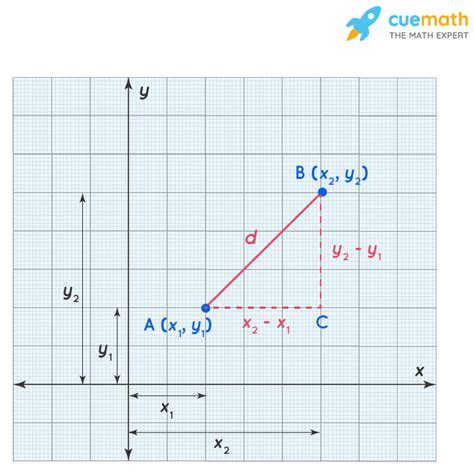
Suppose we have two points, (3, 4) and (6, 8), and we want to calculate the Euclidean distance between them. Using the formula, we get:
=SQRT((6-3)^2+(8-4)^2) =SQRT(3^2+4^2) =SQRT(9+16) =SQRT(25) =5
Therefore, the Euclidean distance between the two points is 5 units.
Applications of Euclidean Distance Formula
The Euclidean distance formula has numerous applications in various fields, including:
- Data analysis and visualization
- Machine learning and artificial intelligence
- Physics and engineering
- Computer science and programming
- Geography and mapping
In data analysis, the Euclidean distance formula is used to calculate the similarity or dissimilarity between data points. It is a measure of how far apart two points are, which can be used to identify patterns, clusters, and relationships in the data.
In machine learning, the Euclidean distance formula is used in algorithms such as k-means clustering and k-nearest neighbors to classify data points into different categories.
In physics and engineering, the Euclidean distance formula is used to calculate the distance between objects, which is crucial in understanding the behavior of physical systems.
In computer science, the Euclidean distance formula is used in programming languages such as Python and R to calculate the distance between data points.
In geography and mapping, the Euclidean distance formula is used to calculate the distance between locations, which is crucial in understanding the relationships between different places.
Advantages and Disadvantages of Euclidean Distance Formula
The Euclidean distance formula has several advantages, including:
- Simple and easy to implement
- Fast and efficient
- Accurate and reliable
However, the Euclidean distance formula also has some disadvantages, including:
- Sensitive to outliers and noise
- Assumes a linear relationship between data points
- Not suitable for high-dimensional data
Despite these limitations, the Euclidean distance formula remains a widely used and powerful tool in data analysis and visualization.
Gallery of Euclidean Distance Formula
Euclidean Distance Formula Image Gallery
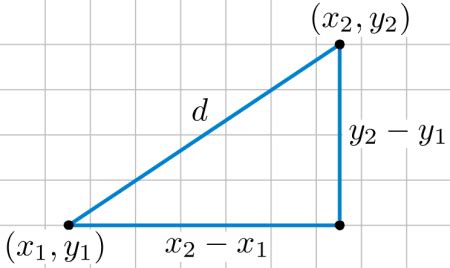

What is the Euclidean distance formula?
+The Euclidean distance formula is a mathematical formula that calculates the distance between two points in a multi-dimensional space.
How to calculate Euclidean distance in Excel?
+To calculate the Euclidean distance in Excel, you can use the formula =SQRT((x2-x1)^2+(y2-y1)^2) or use the Euclidean distance function in the Analysis ToolPak add-in.
What are the advantages and disadvantages of the Euclidean distance formula?
+The advantages of the Euclidean distance formula include its simplicity, speed, and accuracy. However, it is sensitive to outliers and noise, assumes a linear relationship between data points, and is not suitable for high-dimensional data.
In conclusion, the Euclidean distance formula is a powerful tool in data analysis and visualization, with numerous applications in various fields. Its simplicity, speed, and accuracy make it a widely used formula, despite its limitations. By understanding the Euclidean distance formula and its applications, you can gain valuable insights into your data and make informed decisions. We invite you to share your thoughts and experiences with the Euclidean distance formula in the comments below.