5 Ways Average Decimals

Calculating averages is a fundamental mathematical operation that we use in various aspects of life, from statistics and science to everyday decision-making. When dealing with decimals, the process of finding an average, also known as a mean, remains straightforward but requires attention to detail, especially when adding and dividing numbers that are not whole. The importance of accurately calculating averages cannot be overstated, as it directly impacts the reliability of the conclusions we draw from data. Whether in academic research, financial analysis, or personal budgeting, understanding how to work with decimals is crucial.

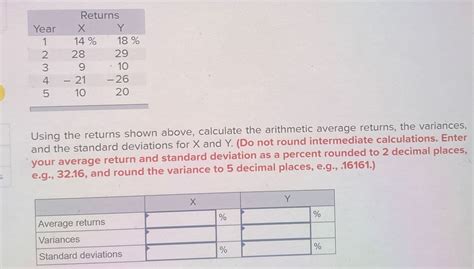
The process of averaging decimals involves summing all the decimal numbers in a dataset and then dividing by the count of the numbers. This simple yet powerful operation helps in understanding the central tendency of a dataset, providing insights into trends, patterns, and outliers. For instance, in finance, calculating the average return on investment (ROI) for a portfolio that includes assets with decimal values (such as stocks or currencies) requires precise handling of decimals to make informed investment decisions.

Moreover, the application of averaging decimals extends beyond numerical analysis into fields like quality control, where the average dimension of a product part might be critical for its functionality and compatibility. In such scenarios, slight deviations in averages can lead to significant differences in performance or even safety. Thus, mastering the calculation of averages, especially with decimals, is not only a mathematical skill but also a valuable tool for making informed decisions across various disciplines.

Averaging Decimals: Basic Principles

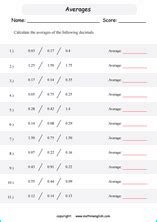
Averaging decimals starts with understanding the basic principle of addition and division. When adding decimals, it's essential to line up the decimal points to ensure that the digits are correctly aligned. This step is critical because it affects the accuracy of the sum. After adding all the numbers, the next step is to divide the sum by the total count of numbers. This division gives the average.

For example, to find the average of 3.5, 2.8, and 4.2, first add these numbers: 3.5 + 2.8 + 4.2 = 10.5. Then, divide the sum by the count of the numbers, which is 3. So, 10.5 / 3 = 3.5. This result means that the average of these three numbers is 3.5.

Step-by-Step Guide to Averaging Decimals

To average decimals, follow these steps: 1. List all the decimal numbers. 2. Add the decimal numbers together, ensuring to line up the decimal points. 3. Count how many numbers are in the list. 4. Divide the sum of the numbers by the count of the numbers. 5. The result of this division is the average of the decimal numbers.

Real-World Applications of Averaging Decimals

Averaging decimals has numerous real-world applications. In education, teachers might calculate the average score of their students on a test that includes decimal-point answers. In sports, the average speed or distance covered by athletes during training can be crucial for optimizing performance. Businesses use averages to understand customer behavior, such as the average amount spent by customers in a store or the average time spent on a website.

Moreover, in environmental science, averages are used to track changes in temperature, sea levels, and other metrics over time. These averages help scientists and policymakers understand the impact of human activities on the environment and make informed decisions about conservation and sustainability efforts.

Common Challenges in Averaging Decimals

One of the common challenges in averaging decimals is ensuring accuracy during the addition and division steps. Rounding errors can occur if the decimals are not handled properly, especially when using calculators or computers that might round numbers differently. Another challenge is dealing with negative decimals, which require careful handling to avoid errors in the calculation.

Tools and Techniques for Averaging Decimals

Several tools and techniques can make averaging decimals easier and more accurate. Spreadsheets, like Microsoft Excel, are powerful tools that can automatically calculate averages, including those of decimal numbers, with high precision. Online calculators specifically designed for statistical calculations can also simplify the process.

For those who prefer manual calculations, using a calculator with a memory function can help in storing the sum of the decimals and then dividing by the count, reducing the chance of error. Additionally, double-checking calculations, especially in critical applications, is a good practice to ensure accuracy.

Best Practices for Accurate Calculations

To ensure accurate calculations when averaging decimals: - Always line up the decimal points when adding numbers. - Use a calculator or computer for complex calculations to minimize human error. - Double-check calculations, especially in applications where accuracy is critical. - Consider rounding the average to a specific decimal place that makes sense for the context of the calculation.

Advanced Topics in Averaging Decimals

Beyond basic averaging, there are advanced topics that involve more complex calculations and considerations. Weighted averages, where some numbers are given more importance than others, require a different approach. Calculating moving averages, which involve averaging a set of numbers over time, can help in smoothing out fluctuations in data and highlighting trends.

In statistical analysis, the average is just one of several measures of central tendency, alongside the median and mode. Understanding when to use each and how they relate to averaging decimals is essential for a deeper analysis of data.

Applications in Data Analysis

In data analysis, averaging decimals is a fundamental skill that underpins more advanced techniques. From data visualization to predictive modeling, accurate averages are crucial for building reliable models and drawing meaningful conclusions. The ability to work with decimals precisely allows analysts to uncover subtle patterns and trends that might be obscured by less precise calculations.

Gallery of Averaging Decimals

Averaging Decimals Image Gallery

Frequently Asked Questions

What is the importance of averaging decimals in real-world applications?

+

Averaging decimals is crucial in various fields, including finance, education, and science, as it helps in understanding trends, making informed decisions, and ensuring accuracy in calculations.

How do you calculate the average of decimal numbers?

+

To calculate the average, add all the decimal numbers together and then divide by the count of the numbers. Ensure to line up the decimal points during addition.

What tools can be used to simplify the process of averaging decimals?

+

Spreadsheets, online calculators, and computers can significantly simplify and accurate the process of averaging decimals, reducing the chance of human error.

In conclusion, averaging decimals is a fundamental mathematical operation with widespread applications across various disciplines. By understanding the principles, tools, and techniques involved, individuals can enhance their ability to work with decimals accurately, leading to better decision-making and analysis. Whether in personal, academic, or professional contexts, mastering the skill of averaging decimals can open up new insights and opportunities, making it an essential skill for anyone looking to navigate and understand the world through data. We invite you to share your thoughts, experiences, and questions about averaging decimals in the comments below, and to explore further resources and tutorials for a deeper dive into this critical mathematical skill.