Intro
Calculating percentages is a fundamental mathematical operation that is used in various aspects of life, including finance, statistics, and everyday problem-solving. Understanding how to work with percentages is crucial for making informed decisions and analyzing data effectively. Here, we'll explore five ways to add percentages, each with its own set of applications and considerations.
The importance of percentage calculations cannot be overstated. In finance, for instance, percentages are used to calculate interest rates, investment returns, and discounts. In statistics, percentages help in understanding proportions and trends within data sets. Moreover, in everyday life, percentages are used to compare prices, calculate tips, and understand nutritional information. Given the widespread application of percentages, it's essential to grasp the different methods of adding them together.
Whether you're a student looking to improve your mathematical skills, a professional seeking to enhance your data analysis capabilities, or simply an individual aiming to make more informed financial decisions, understanding how to add percentages is a valuable skill. The methods outlined below cater to different scenarios and levels of complexity, ensuring that readers can apply them to a variety of situations.
Introduction to Percentage Calculations

Before diving into the methods of adding percentages, it's essential to understand the basics of percentage calculations. A percentage is a fraction or ratio in which the denominator is 100. It is often denoted using the percent sign, "%". To calculate a percentage, you divide the part by the whole and then multiply by 100. For example, if you want to find 20% of 50, you would calculate (20/100) * 50 = 10.
Method 1: Adding Percentages to a Base Number
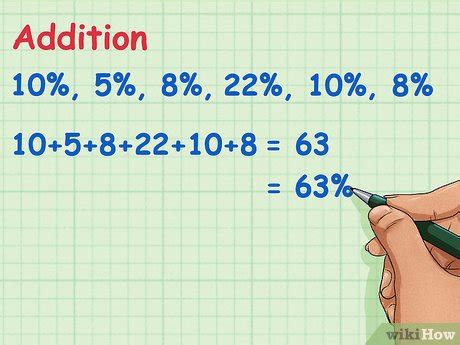
The first method involves adding percentages to a base number. This is commonly used in scenarios where you're applying successive discounts or increases to an initial value. For instance, if you have a product priced at $100 and you apply a 10% discount followed by a 20% discount, you would first calculate the price after the first discount: $100 - (10% of $100) = $100 - $10 = $90. Then, you apply the second discount: $90 - (20% of $90) = $90 - $18 = $72.
Step-by-Step Process
- Identify the base number.
- Calculate the first percentage of the base number.
- Subtract or add the calculated percentage from/to the base number to get the new value.
- Repeat steps 2 and 3 for each successive percentage.
Method 2: Combining Percentages

The second method involves combining percentages directly. This is useful when you need to find the total effect of multiple percentage changes without knowing the base number. For example, if you want to combine a 10% increase and a 20% increase, you can add the percentages but also need to account for the compounding effect. The formula to combine percentages is: Total Percentage Change = (1 + Percentage 1) * (1 + Percentage 2) - 1.
Example Calculation
- Percentage 1: 10% or 0.10
- Percentage 2: 20% or 0.20
- Total Percentage Change = (1 + 0.10) * (1 + 0.20) - 1 = 1.10 * 1.20 - 1 = 1.32 - 1 = 0.32 or 32%
Method 3: Using Decimal Forms

The third method involves converting percentages to their decimal forms and then performing operations. This is particularly useful for calculating percentages of percentages or for combining percentages in complex scenarios. To convert a percentage to a decimal, divide by 100. For example, 25% becomes 0.25.
Application in Calculations
- To find 25% of 200: 0.25 * 200 = 50
- To apply a 10% discount and then a 15% tax on a $100 item:
- Discount: $100 * 0.10 = $10, Price after discount = $100 - $10 = $90
- Tax: $90 * 0.15 = $13.50, Final price = $90 + $13.50 = $103.50
Method 4: Successive Percentage Changes

The fourth method deals with successive percentage changes, where each change is applied to the result of the previous change. This is common in financial calculations, such as calculating the future value of an investment with annual interest rates. The formula for successive percentage changes is: Final Value = Initial Value * (1 + Percentage Change 1) * (1 + Percentage Change 2) *... * (1 + Percentage Change N).
Example of Successive Changes
- Initial investment: $1,000
- Annual interest rate: 5% for the first year, 10% for the second year
- Value after first year = $1,000 * (1 + 0.05) = $1,050
- Value after second year = $1,050 * (1 + 0.10) = $1,155
Method 5: Geometric Progression

The fifth method involves using geometric progression to model scenarios where percentages are compounded over time or iterations. This is particularly useful in population growth models, chemical reactions, or any situation where the rate of change is proportional to the current value. The formula for the nth term of a geometric progression is: an = a1 * r^(n-1), where a1 is the first term, r is the common ratio (1 + percentage change in decimal form), and n is the term number.
Geometric Progression Example
- Initial population: 100
- Annual growth rate: 20%
- Population after 5 years = 100 * (1 + 0.20)^5
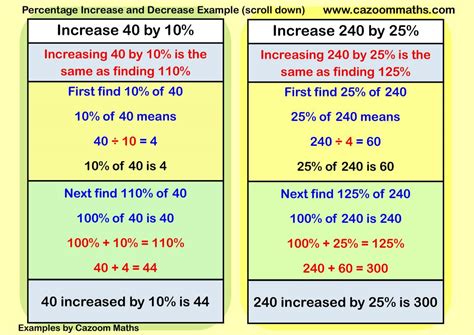
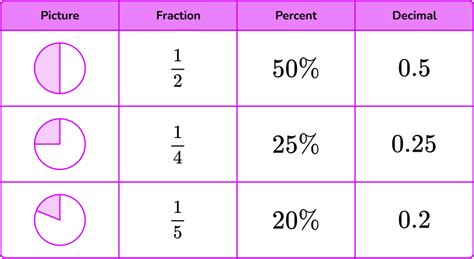
Gallery of Percentage Calculations
Percentage Calculations Image Gallery







Frequently Asked Questions
What is the formula to calculate a percentage of a number?
+The formula to find a percentage of a number is: (Percentage / 100) * Number.
How do you add two percentages together?
+To add two percentages, convert them to decimals by dividing by 100, add them together, and then convert back to a percentage by multiplying by 100.
What is the difference between a percentage increase and a percentage decrease?
+A percentage increase adds a percentage of the original value to itself, while a percentage decrease subtracts a percentage of the original value from itself.
Understanding and applying these methods for adding percentages can significantly enhance your ability to analyze and solve problems in various fields. Whether it's calculating discounts, understanding investment growth, or comparing statistical data, mastering percentage calculations is a fundamental skill that can benefit you in numerous ways. By practicing these methods and applying them to real-world scenarios, you can develop a deeper understanding of how percentages work and how they can be used to make informed decisions. If you have any further questions or would like to explore more topics related to percentage calculations, feel free to comment or share your thoughts.