Find Interquartile Range Excel

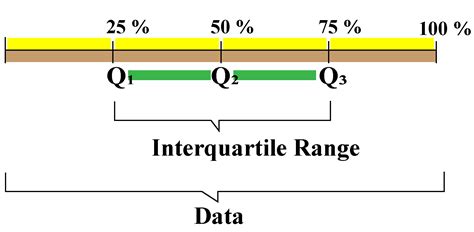
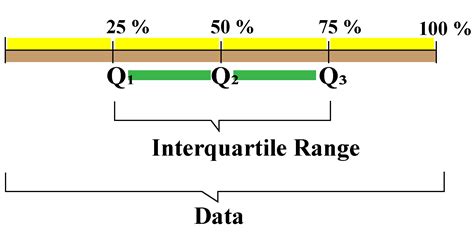
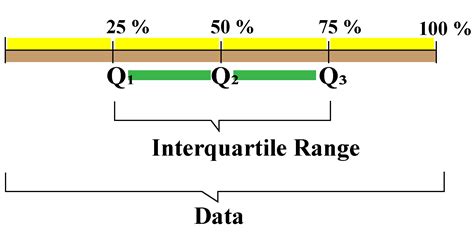
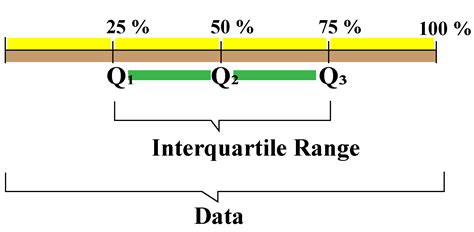
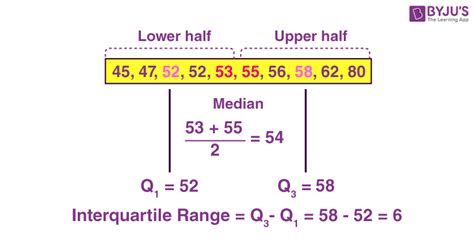
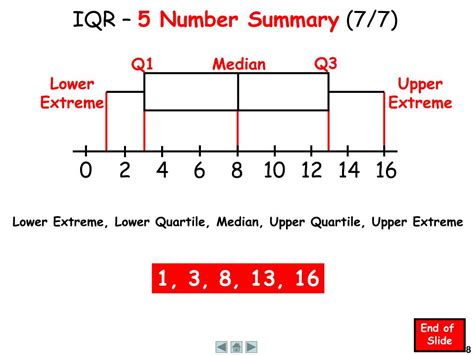
The interquartile range (IQR) is a statistical measure that represents the difference between the 75th percentile (Q3) and the 25th percentile (Q1) of a dataset. It is a useful tool for identifying outliers and understanding the spread of data. In Excel, you can calculate the IQR using various methods. Here, we will explore the different ways to find the IQR in Excel.

To begin with, let's consider the importance of understanding data distribution. The IQR is a valuable metric that helps us grasp the dispersion of data, making it an essential concept in statistics and data analysis. By calculating the IQR, we can determine the range of the middle 50% of the data, which is vital in identifying outliers and skewed distributions.

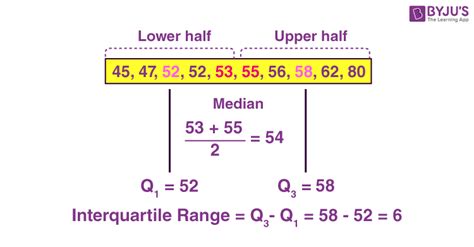
The interquartile range is a crucial concept in statistics, and its calculation is relatively straightforward. The IQR is calculated as the difference between the third quartile (Q3) and the first quartile (Q1). The first quartile is the median of the lower half of the data, while the third quartile is the median of the upper half of the data. By subtracting the first quartile from the third quartile, we obtain the IQR, which represents the range of the middle 50% of the data.

Method 1: Using the QUARTILE Function

The QUARTILE function in Excel returns the specified quartile of a dataset. To calculate the IQR, you can use the following formula: =QUARTILE(range, 3) - QUARTILE(range, 1) Where "range" is the range of cells containing the data.

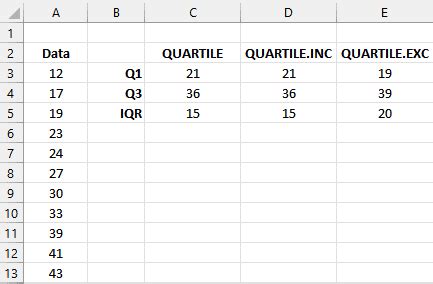
Example:

Suppose we have a dataset in the range A1:A10. To calculate the IQR, we can use the following formula: =QUARTILE(A1:A10, 3) - QUARTILE(A1:A10, 1) This formula returns the difference between the 75th percentile (Q3) and the 25th percentile (Q1) of the dataset.

Method 2: Using the PERCENTILE Function

The PERCENTILE function in Excel returns the specified percentile of a dataset. To calculate the IQR, you can use the following formula: =PERCENTILE(range, 0.75) - PERCENTILE(range, 0.25) Where "range" is the range of cells containing the data.

Example:

Suppose we have a dataset in the range A1:A10. To calculate the IQR, we can use the following formula: =PERCENTILE(A1:A10, 0.75) - PERCENTILE(A1:A10, 0.25) This formula returns the difference between the 75th percentile (Q3) and the 25th percentile (Q1) of the dataset.

Method 3: Using the Quartile Function in the Analysis ToolPak

The Analysis ToolPak in Excel provides a built-in function for calculating quartiles. To calculate the IQR using this method, follow these steps: 1. Go to the "Data" tab in the ribbon. 2. Click on "Data Analysis" in the "Analysis" group. 3. Select "Quartiles" from the list of available functions. 4. Enter the range of cells containing the data in the "Input Range" field. 5. Click "OK" to calculate the quartiles.

The output will include the first quartile (Q1), the third quartile (Q3), and the interquartile range (IQR).

Method 4: Using a Formula with the MEDIAN Function

You can also calculate the IQR using a formula that involves the MEDIAN function. The formula is as follows: =MEDIAN(LARGE(range, ROW(INDIRECT("1:" & COUNT(range)/2)))) - MEDIAN(SMALL(range, ROW(INDIRECT("1:" & COUNT(range)/2)))) Where "range" is the range of cells containing the data.

Example:

Suppose we have a dataset in the range A1:A10. To calculate the IQR, we can use the following formula: =MEDIAN(LARGE(A1:A10, ROW(INDIRECT("1:" & COUNT(A1:A10)/2)))) - MEDIAN(SMALL(A1:A10, ROW(INDIRECT("1:" & COUNT(A1:A10)/2)))) This formula returns the difference between the 75th percentile (Q3) and the 25th percentile (Q1) of the dataset.

Method 5: Using a User-Defined Function (UDF)

You can create a user-defined function (UDF) in Excel to calculate the IQR. To do this, follow these steps: 1. Open the Visual Basic Editor (VBE) by pressing "Alt + F11" or by navigating to "Developer" > "Visual Basic" in the ribbon. 2. In the VBE, click "Insert" > "Module" to insert a new module. 3. Paste the following code into the module: Function IQR(range As Range) As Double IQR = Application.WorksheetFunction.Quartile(range, 3) - Application.WorksheetFunction.Quartile(range, 1) End Function 4. Save the module by clicking "File" > "Save" (or press "Ctrl + S"). 5. Return to the Excel worksheet and enter the following formula: =IQR(A1:A10) Where "A1:A10" is the range of cells containing the data.

The UDF will return the IQR of the dataset.

Interquartile Range Image Gallery

What is the interquartile range (IQR)?

+

The interquartile range (IQR) is a statistical measure that represents the difference between the 75th percentile (Q3) and the 25th percentile (Q1) of a dataset.

Why is the IQR important in statistics?

+

The IQR is important in statistics because it helps to identify outliers and understand the spread of data. It is also useful for comparing the distribution of different datasets.

How do I calculate the IQR in Excel?

+

There are several ways to calculate the IQR in Excel, including using the QUARTILE function, the PERCENTILE function, and the Analysis ToolPak. You can also create a user-defined function (UDF) to calculate the IQR.

In conclusion, the interquartile range is a valuable statistical measure that helps us understand the spread of data and identify outliers. By using the methods outlined in this article, you can easily calculate the IQR in Excel and gain a deeper insight into your data. Whether you are a statistician, data analyst, or simply looking to improve your Excel skills, understanding the IQR is an essential part of data analysis. We hope this article has provided you with a comprehensive understanding of the interquartile range and its calculation in Excel. If you have any further questions or would like to share your experiences with calculating the IQR, please feel free to comment below.