Normal Distributions Worksheet 12 7

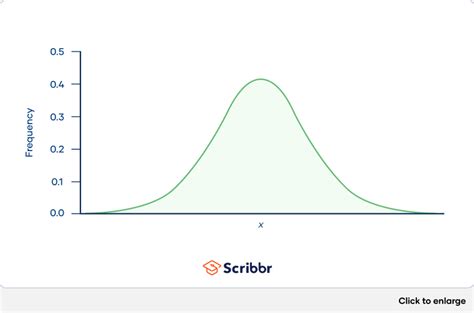
Understanding normal distributions is crucial in statistics, as they describe how data points are distributed in a dataset. A normal distribution, also known as a Gaussian distribution or bell curve, is a probability distribution that is symmetric about the mean, indicating that data near the mean are more frequent in occurrence than data far from the mean. In this article, we will delve into the concept of normal distributions, their characteristics, how to work with them, and provide practical examples and statistical data to enhance understanding.

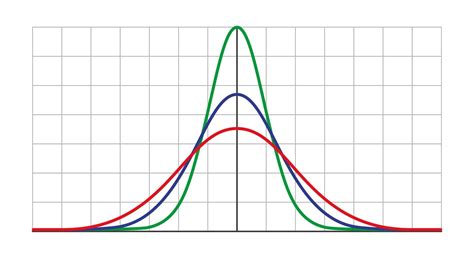
Normal distributions are fundamental in statistical analysis because many natural phenomena, such as heights, weights, and IQ scores, tend to follow this pattern. The normal distribution is defined by its mean (μ) and standard deviation (σ), which determine the center and the spread of the distribution, respectively. Knowing how to calculate probabilities using the normal distribution is essential for making predictions and understanding variability in data.

The importance of normal distributions cannot be overstated, especially in fields like medicine, social sciences, and engineering, where understanding the distribution of data is critical for research and decision-making. For instance, in medicine, the distribution of blood pressure or cholesterol levels in a population can inform healthcare policies and interventions. In social sciences, understanding the distribution of income or education levels can help in formulating social and economic policies.

Characteristics of Normal Distributions

Normal distributions have several key characteristics. They are symmetric about the mean, showing that data points are equally likely to be above or below the mean. The mean, median, and mode are all located at the center of the distribution. The area under the entire curve is equal to 1, which represents the total probability of all possible outcomes. The standard deviation determines the spread of the distribution, with about 68% of the data falling within one standard deviation of the mean, about 95% within two standard deviations, and about 99.7% within three standard deviations.

Working with Normal Distributions

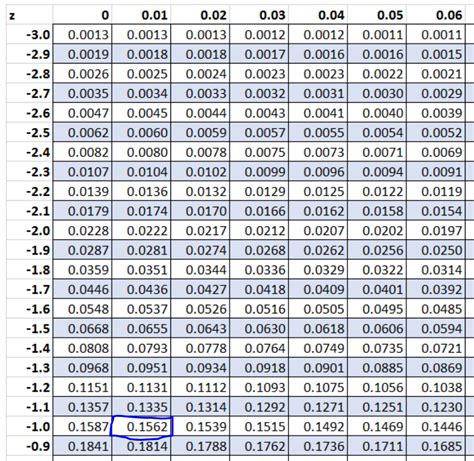
Working with normal distributions involves understanding how to calculate probabilities, which can be done using z-scores or standard scores. A z-score tells us how many standard deviations away from the mean our data point is. The formula for calculating a z-score is (z = \frac{X - \mu}{\sigma}), where (X) is the value of the element, (\mu) is the mean of the dataset, and (\sigma) is the standard deviation. Once we have the z-score, we can use a standard normal distribution table (also known as a z-table) to find the probability.

Steps for Calculating Probabilities

Identify the Mean and Standard Deviation: Know the mean ((\mu)) and standard deviation ((\sigma)) of the distribution.
Calculate the Z-Score: Use the formula (z = \frac{X - \mu}{\sigma}) to find the z-score for a given value (X).
Use the Z-Table: Look up the z-score in the standard normal distribution table to find the corresponding probability.

Practical Examples and Statistical Data

Let's consider a practical example: The average height of adult men in a certain country is 175 cm with a standard deviation of 6 cm. What is the probability that a randomly selected man is between 165 cm and 185 cm tall? First, we calculate the z-scores for 165 cm and 185 cm. For 165 cm, (z = \frac{165 - 175}{6} = -1.67). For 185 cm, (z = \frac{185 - 175}{6} = 1.67). Using the z-table, we find the probabilities corresponding to these z-scores and subtract them to find the probability of a man being between 165 cm and 185 cm tall.

Benefits of Understanding Normal Distributions

Improved Data Analysis: Understanding normal distributions helps in analyzing data more effectively, making it easier to identify patterns and outliers.
Better Decision Making: By knowing how data is distributed, individuals can make more informed decisions in various fields, from business to healthcare.
Enhanced Research: Normal distributions are crucial in research for hypothesis testing and confidence intervals, allowing researchers to draw meaningful conclusions from their data.

Challenges and Limitations

While normal distributions are powerful tools, there are challenges and limitations to their application. Not all data follows a normal distribution, and assuming normality when it does not exist can lead to incorrect conclusions. Additionally, calculating probabilities requires accurate estimates of the mean and standard deviation, which can be challenging with small or skewed datasets.

Real-World Applications

Quality Control: In manufacturing, understanding the distribution of product dimensions or quality metrics helps in setting standards and controlling variability.
Financial Analysis: Normal distributions are used in finance to model stock prices and returns, helping investors understand and manage risk.
Medical Research: In medical studies, the distribution of outcomes (e.g., blood pressure reduction) is crucial for evaluating the effectiveness of treatments.

Conclusion and Future Directions

In conclusion, normal distributions are a cornerstone of statistical analysis, offering insights into the behavior of data. As data analysis becomes increasingly important across all sectors, understanding normal distributions will remain a vital skill. Future directions include the development of more sophisticated models that can handle complex, non-normal data distributions, and the integration of machine learning techniques with traditional statistical methods.

Final Thoughts

Understanding and working with normal distributions is a skill that requires practice and patience. By grasping the concepts and applying them to real-world problems, individuals can unlock the full potential of data analysis, leading to better decisions and outcomes in various fields.

Normal Distributions Image Gallery

What is a Normal Distribution?

A normal distribution, also known as a Gaussian distribution or bell curve, is a probability distribution that is symmetric about the mean, indicating that data near the mean are more frequent in occurrence than data far from the mean.

How Do You Calculate the Z-Score?

The z-score is calculated using the formula \(z = \frac{X - \mu}{\sigma}\), where \(X\) is the value of the element, \(\mu\) is the mean of the dataset, and \(\sigma\) is the standard deviation.

What Are the Applications of Normal Distributions?

Normal distributions have applications in quality control, financial analysis, medical research, and more, helping in understanding and analyzing data, making predictions, and informing decision-making.

We hope this comprehensive guide to normal distributions has been informative and helpful. Whether you are a student, researcher, or professional, understanding normal distributions can enhance your ability to analyze and interpret data. Share your thoughts, questions, or experiences with normal distributions in the comments below, and feel free to share this article with others who might find it useful. Together, we can continue to explore and apply the principles of statistics to make sense of our world.