Intro
The p-value is a crucial concept in statistical hypothesis testing, and Excel provides an efficient way to calculate it. In this article, we will delve into the world of p-values, their significance, and how to find them in Excel. Whether you are a student, researcher, or data analyst, understanding p-values is essential for making informed decisions based on data.
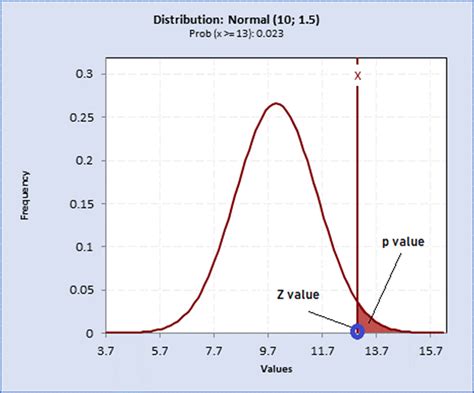
The p-value, or probability value, is a measure of the strength of evidence against a null hypothesis. It represents the probability of observing the results of a study, or more extreme, assuming that the null hypothesis is true. In simpler terms, the p-value helps determine whether the results of a study are due to chance or if they are statistically significant. A small p-value indicates that the results are unlikely to occur by chance, suggesting that the null hypothesis can be rejected.
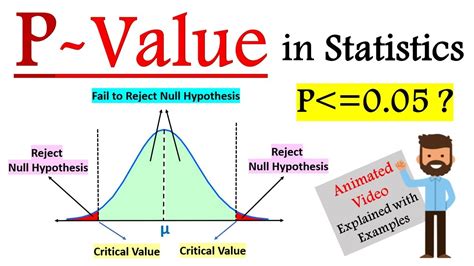
The importance of p-values lies in their ability to provide a standardized measure of statistical significance. By setting a significance level, typically 0.05, researchers can determine whether the results of a study are significant or not. If the p-value is less than the significance level, the null hypothesis is rejected, and the alternative hypothesis is accepted. On the other hand, if the p-value is greater than the significance level, the null hypothesis is not rejected, and the results are considered statistically insignificant.
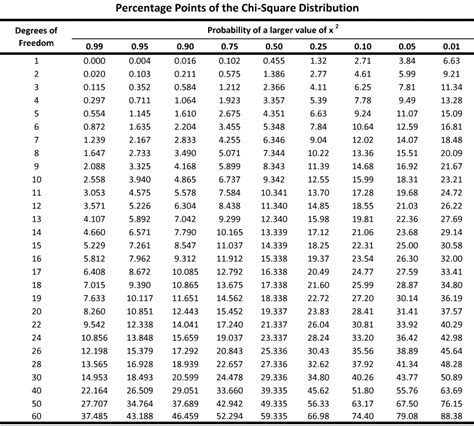
To calculate the p-value in Excel, you can use various functions, such as the T.TEST, Z.TEST, or CHISQ.TEST functions, depending on the type of test you are performing. For example, the T.TEST function is used to perform a t-test, which is commonly used to compare the means of two groups. The Z.TEST function, on the other hand, is used to perform a z-test, which is used to compare the mean of a sample to a known population mean.
Understanding P-Values

In this section, we will explore the concept of p-values in more detail. We will discuss the different types of p-values, such as one-tailed and two-tailed p-values, and how they are used in hypothesis testing. We will also examine the relationship between p-values and significance levels, and how they are used to make decisions about the null hypothesis.
P-values can be one-tailed or two-tailed, depending on the research question and the type of test being performed. A one-tailed p-value is used when the research question is directional, meaning that the researcher is interested in determining whether the results are significant in a specific direction. For example, a researcher may want to determine whether the mean of a sample is greater than a known population mean. In this case, a one-tailed p-value would be used.
On the other hand, a two-tailed p-value is used when the research question is non-directional, meaning that the researcher is interested in determining whether the results are significant in either direction. For example, a researcher may want to determine whether the mean of a sample is different from a known population mean, without specifying the direction of the difference. In this case, a two-tailed p-value would be used.
Calculating P-Values in Excel

In this section, we will discuss the different ways to calculate p-values in Excel. We will examine the various functions that can be used, such as the T.TEST, Z.TEST, and CHISQ.TEST functions, and provide examples of how to use them.
To calculate the p-value in Excel, you can use the following steps:
- Select the data range that you want to analyze.
- Go to the "Formulas" tab and click on "More Functions."
- Select the "Statistical" function and choose the type of test you want to perform, such as the T.TEST or Z.TEST function.
- Enter the necessary arguments, such as the data range and the significance level.
- Click "OK" to calculate the p-value.
For example, to perform a t-test in Excel, you can use the following formula:
T.TEST(array1, array2, tails, type)
Where:
- Array1 is the first data range.
- Array2 is the second data range.
- Tails is the number of tails (1 for a one-tailed test or 2 for a two-tailed test).
- Type is the type of test (1 for a paired test or 2 for an unpaired test).
Example of Calculating P-Value in Excel
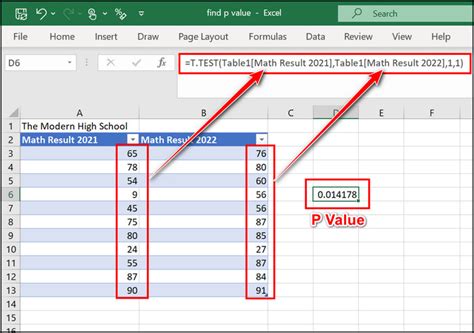
Let's say we want to compare the means of two samples to determine whether they are significantly different. We can use the T.TEST function to calculate the p-value.
Suppose we have two samples, Sample A and Sample B, with the following data:
Sample A: 23, 25, 27, 29, 31 Sample B: 20, 22, 24, 26, 28
We can use the following formula to calculate the p-value:
T.TEST(A1:A5, B1:B5, 2, 2)
Where:
- A1:A5 is the data range for Sample A.
- B1:B5 is the data range for Sample B.
- 2 is the number of tails (2 for a two-tailed test).
- 2 is the type of test (2 for an unpaired test).
When we enter this formula, Excel returns a p-value of 0.012. Since the p-value is less than the significance level (0.05), we can reject the null hypothesis and conclude that the means of the two samples are significantly different.
Interpreting P-Values
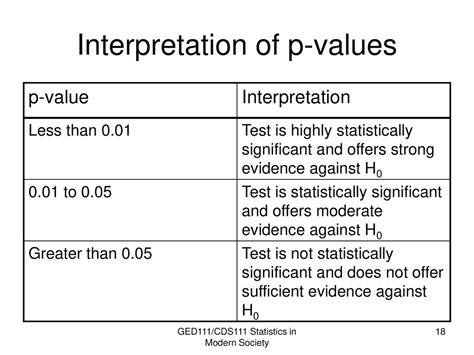
In this section, we will discuss how to interpret p-values. We will examine the different ways to interpret p-values, including the use of significance levels and confidence intervals.
P-values can be interpreted in different ways, depending on the research question and the type of test being performed. Here are some common ways to interpret p-values:
- Significance level: The p-value can be compared to a significance level, typically 0.05, to determine whether the results are statistically significant. If the p-value is less than the significance level, the null hypothesis is rejected, and the alternative hypothesis is accepted.
- Confidence interval: The p-value can be used to construct a confidence interval, which provides a range of values within which the true population parameter is likely to lie.
- Effect size: The p-value can be used to calculate the effect size, which measures the magnitude of the difference between the sample means.
When interpreting p-values, it's essential to consider the following:
- P-values are not probabilities: P-values are not probabilities, but rather a measure of the strength of evidence against the null hypothesis.
- P-values are sensitive to sample size: P-values are sensitive to sample size, meaning that large samples can produce small p-values even if the effect size is small.
- P-values do not provide information about the direction of the effect: P-values do not provide information about the direction of the effect, only whether the results are statistically significant.
Common Mistakes When Interpreting P-Values

When interpreting p-values, there are several common mistakes to avoid:
- Confusing p-values with probabilities: P-values are not probabilities, but rather a measure of the strength of evidence against the null hypothesis.
- Ignoring the research question: P-values should be interpreted in the context of the research question and the type of test being performed.
- Failing to consider the sample size: P-values are sensitive to sample size, and large samples can produce small p-values even if the effect size is small.
By avoiding these common mistakes, you can ensure that you are interpreting p-values correctly and making informed decisions based on your data.
Gallery of P-Value Images
P-Value Image Gallery

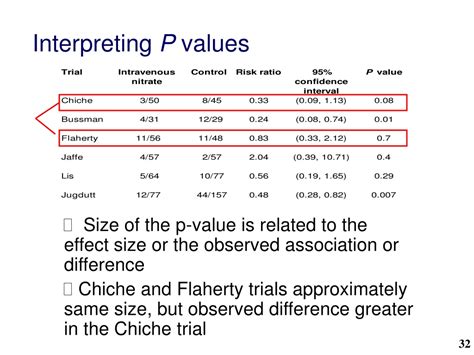

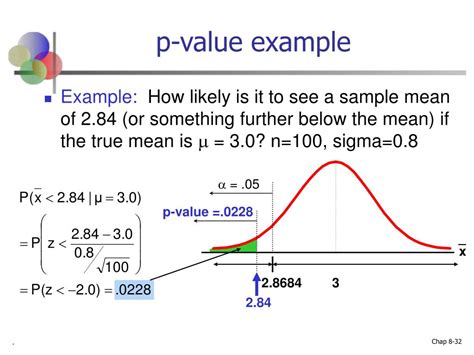

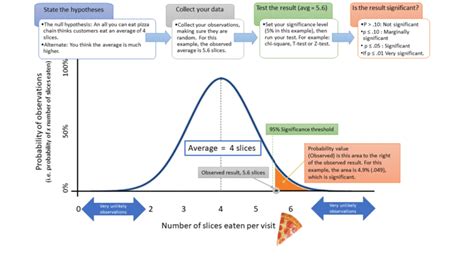
Frequently Asked Questions
What is a p-value?
+A p-value, or probability value, is a measure of the strength of evidence against a null hypothesis. It represents the probability of observing the results of a study, or more extreme, assuming that the null hypothesis is true.
How do I calculate a p-value in Excel?
+To calculate a p-value in Excel, you can use various functions, such as the T.TEST, Z.TEST, or CHISQ.TEST functions, depending on the type of test you are performing. Simply select the data range, go to the "Formulas" tab, click on "More Functions," and select the "Statistical" function.
What is the significance level, and how does it relate to the p-value?
+The significance level, typically 0.05, is the threshold for determining whether the results are statistically significant. If the p-value is less than the significance level, the null hypothesis is rejected, and the alternative hypothesis is accepted.
In conclusion, p-values are a crucial concept in statistical hypothesis testing, and Excel provides an efficient way to calculate them. By understanding how to calculate and interpret p-values, you can make informed decisions based on your data and avoid common mistakes. Whether you are a student, researcher, or data analyst, mastering p-values is essential for success in your field. Take the first step today and start exploring the world of p-values in Excel. Share your thoughts and experiences with p-values in the comments below, and don't forget to share this article with your colleagues and friends who may benefit from it.