Normal Probability Plot In Excel

Normal probability plots are a crucial tool in statistics for assessing whether a dataset follows a normal distribution. Excel, being a widely used spreadsheet software, offers various methods to create these plots. Understanding normal probability plots is essential in data analysis, as many statistical tests assume normality. In this article, we will delve into the importance of normal probability plots, how to create them in Excel, and interpret their results.

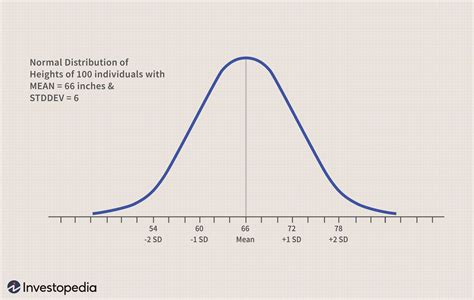
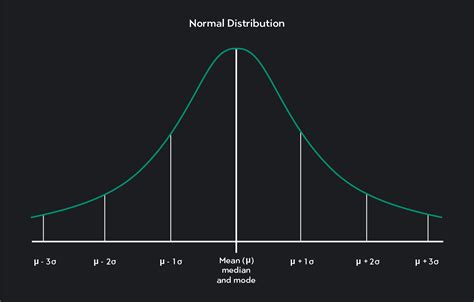
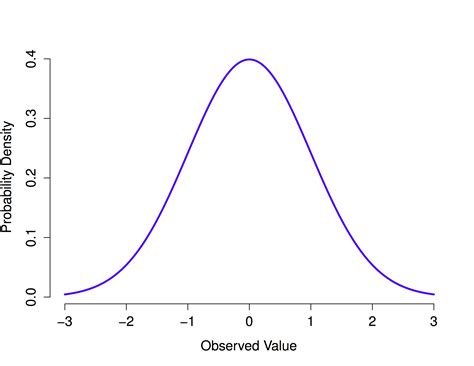
The normal distribution, also known as the Gaussian distribution, is symmetric about its mean, showing that data near the mean are more frequent in occurrence than data far from the mean. In a normal distribution, about 68% of the data falls within one standard deviation of the mean, about 95% falls within two standard deviations, and about 99.7% falls within three standard deviations. This distribution is crucial in statistical analysis because many statistical procedures assume that the data follow a normal distribution.

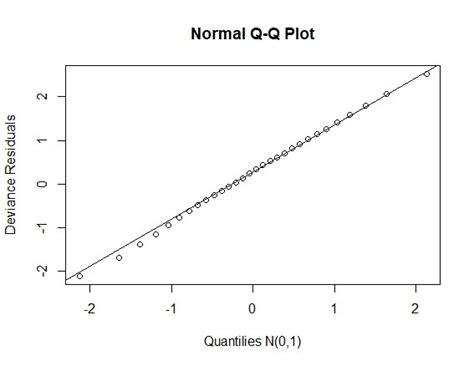
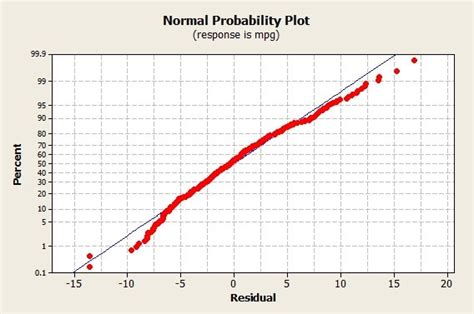
Normal probability plots, also known as Q-Q plots (Quantile-Quantile plots), are used to determine whether a dataset is approximately normally distributed. These plots compare the quantiles of the dataset to the quantiles of a normal distribution. If the dataset is normally distributed, the points on the Q-Q plot will lie close to a straight line. Deviations from this line indicate non-normality.

Importance of Normal Probability Plots

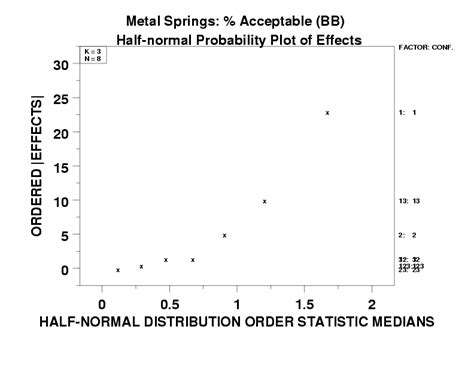
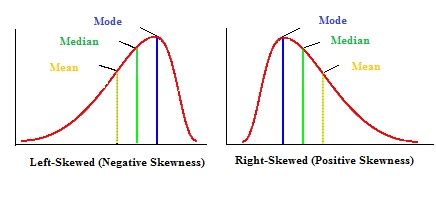
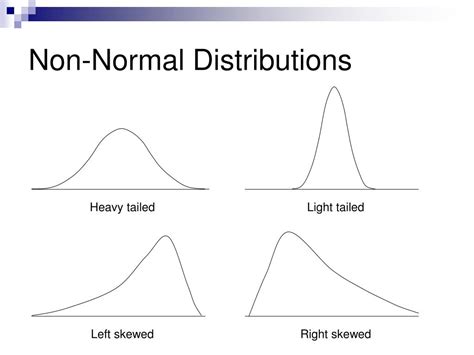
Normal probability plots are vital for several reasons. First, they help in identifying outliers, which are data points that are significantly different from other observations. Outliers can affect the mean and standard deviation of a dataset, potentially leading to incorrect conclusions if not addressed. Second, these plots aid in checking for skewness and kurtosis. Skewness refers to the asymmetry of the probability distribution, while kurtosis refers to how tailed or flat the distribution is compared to a normal distribution. Significant skewness or kurtosis can indicate non-normality. Lastly, normal probability plots are useful in deciding whether to use parametric or non-parametric statistical tests. Parametric tests, which are more powerful, assume normality, while non-parametric tests do not require normality but are generally less powerful.

Creating Normal Probability Plots in Excel

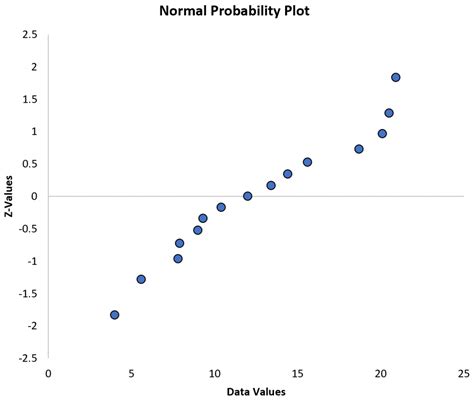
To create a normal probability plot in Excel, you can follow these steps:

1. Prepare Your Data: Ensure your data is in a single column.
2. Rank Your Data: Rank your data in ascending order. You can use the RANK.AVG function for this purpose.
3. Calculate Quantiles: Calculate the quantiles of your data. This can be done using the QUARTILE function for quartiles or the PERCENTRANK function for percentiles.
4. Calculate Theoretical Quantiles: Calculate the theoretical quantiles from a standard normal distribution that correspond to your data's quantiles. This involves using the NORM.S.INV function.
5. Plot the Data: Plot the theoretical quantiles against your data's quantiles. If the points lie close to a straight line, your data is likely normally distributed.

Step-by-Step Guide

For a more detailed approach, consider the following: - **Step 1**: Enter your data into a column, say A1:A100. - **Step 2**: In column B, rank your data using the formula `=RANK.AVG(A2,$A$2:$A$100)`, and copy it down. - **Step 3**: Calculate the quantiles in column C using the formula `=(B2-0.5)/COUNT($A$2:$A$100)`, and copy it down. - **Step 4**: In column D, calculate the theoretical quantiles using the formula `=NORM.S.INV(C2)`, and copy it down. - **Step 5**: Plot the values in column D against the values in column A.

Interpreting Normal Probability Plots

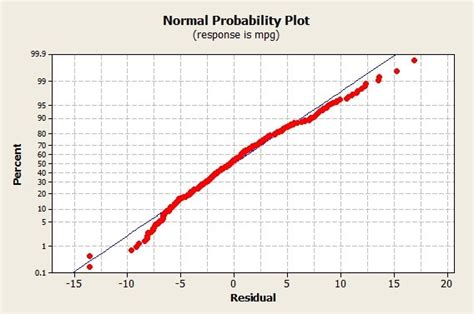
Interpreting a normal probability plot involves checking how closely the points adhere to a straight line. Here are some guidelines:

• Linear Pattern: If the points form a linear pattern, the data is likely to be normally distributed.
• Curvature: If the points show curvature, it may indicate non-normality, such as skewness.
• Outliers: Points that significantly deviate from the line could be outliers.
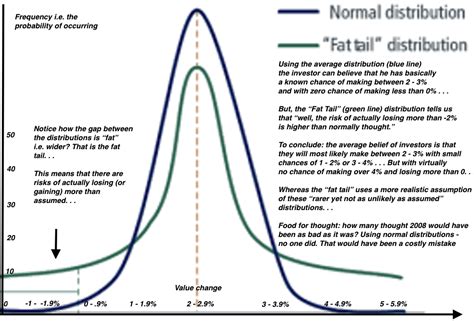
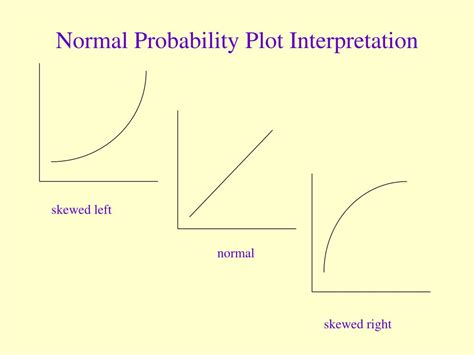
• S-Curves or Other Patterns: These can indicate various forms of non-normality, such as bimodality.

Common Patterns and Their Interpretations

- **S-Shaped Curve**: Indicates heavy-tailed distributions. - **C-Shaped Curve**: Suggests light-tailed distributions. - **Points Falling Off at the Ends**: Could indicate outliers or heavy-tailed distributions.

Practical Applications

Normal probability plots have numerous practical applications across various fields, including:

• Quality Control: To monitor the quality of products and ensure they meet certain standards.
• Finance: In risk analysis and portfolio management to understand the distribution of returns.
• Medical Research: To analyze the distribution of outcomes or the effect of treatments.
• Engineering: In reliability analysis to predict the lifespan of components.

Example Use Cases

- **Analyzing Stock Prices**: To determine if the daily returns of a stock follow a normal distribution. - **Quality Control in Manufacturing**: To check if the dimensions of a product are normally distributed.

Gallery of Normal Probability Plot Examples

Normal Probability Plot Examples

Frequently Asked Questions

What is a normal probability plot used for?

+

A normal probability plot is used to determine if a dataset is normally distributed, which is crucial for many statistical analyses.

How do I create a normal probability plot in Excel?

+

You can create a normal probability plot in Excel by ranking your data, calculating quantiles, finding theoretical quantiles from a standard normal distribution, and then plotting these against your data's quantiles.

What does it mean if my data points do not lie on a straight line in a normal probability plot?

+

If your data points do not lie on a straight line, it indicates that your data may not be normally distributed. This could be due to skewness, outliers, or other forms of non-normality.

Can I use normal probability plots for non-continuous data?

+

Normal probability plots are typically used for continuous data. For non-continuous or categorical data, other methods such as histograms or bar charts might be more appropriate.

What are some common patterns seen in normal probability plots that indicate non-normality?

+

Common patterns include S-curves, which can indicate heavy-tailed distributions, and C-curves, suggesting light-tailed distributions. Outliers and significant curvature also indicate non-normality.

To summarize, normal probability plots are a powerful tool in statistical analysis for assessing normality, which is a fundamental assumption in many statistical tests. Understanding how to create and interpret these plots in Excel can significantly enhance your data analysis capabilities. Whether you're in quality control, finance, medical research, or any field that involves data analysis, mastering normal probability plots can help you make more informed decisions based on your data. We encourage you to practice creating these plots with your own datasets and to explore the wide range of applications they have in real-world scenarios. Share your experiences or questions about normal probability plots in the comments below, and don't forget to share this article with anyone who might benefit from learning about this valuable statistical tool.