5 Ways To Calculate Sharpe Ratio

The Sharpe Ratio is a widely used metric in finance that helps investors understand the relationship between risk and return of an investment. It is calculated by subtracting the risk-free rate from the expected return of an investment and then dividing the result by the standard deviation of the investment's returns. In this article, we will delve into the world of Sharpe Ratio, exploring its importance, benefits, and most importantly, how to calculate it using different methods.

The Sharpe Ratio is essential for investors as it provides a clear picture of an investment's performance, taking into account both the returns and the risks involved. A higher Sharpe Ratio indicates that an investment has generated excess returns relative to the risk taken, making it a more attractive option for investors. With the increasing complexity of financial markets, understanding the Sharpe Ratio has become crucial for making informed investment decisions. In the following sections, we will discuss the different methods of calculating the Sharpe Ratio, providing a comprehensive overview of this vital metric.

Introduction to Sharpe Ratio Calculation

The Sharpe Ratio is calculated using the following formula: (Expected Return - Risk-Free Rate) / Standard Deviation. The expected return is the average return of an investment over a certain period, the risk-free rate is the return of a risk-free asset such as a U.S. Treasury bond, and the standard deviation is a measure of the investment's volatility. To calculate the Sharpe Ratio, we need to have these three components. In the next section, we will explore the first method of calculating the Sharpe Ratio.

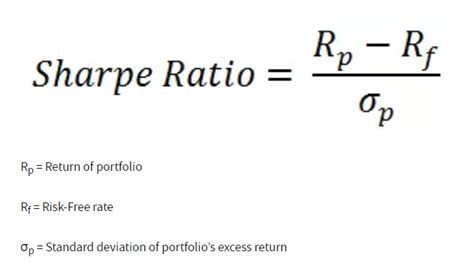
Method 1: Using Historical Data

The first method of calculating the Sharpe Ratio involves using historical data. This method requires us to have access to the investment's past returns, which can be obtained from financial databases or the investment's website. We then calculate the average return and standard deviation of the investment's returns over a certain period. The risk-free rate is typically obtained from a reliable source such as the U.S. Treasury Department. Once we have these components, we can plug them into the Sharpe Ratio formula to get the result.

For example, let's say we want to calculate the Sharpe Ratio of a stock using 5 years of historical data. We obtain the monthly returns of the stock and calculate the average return, which is 10%. We also calculate the standard deviation of the returns, which is 15%. The risk-free rate is 2%. Using the Sharpe Ratio formula, we get: (0.10 - 0.02) / 0.15 = 0.53. This means that the stock has generated a Sharpe Ratio of 0.53, indicating that it has provided a moderate level of excess returns relative to the risk taken.

Benefits of Using Historical Data

Using historical data to calculate the Sharpe Ratio has several benefits. Firstly, it allows us to use real data, which reflects the actual performance of the investment. Secondly, it enables us to calculate the Sharpe Ratio over different time periods, providing a more comprehensive picture of the investment's performance. However, it also has some limitations, such as the potential for data biases and the assumption that past performance will continue in the future.

Method 2: Using Expected Returns

The second method of calculating the Sharpe Ratio involves using expected returns. This method requires us to have an estimate of the investment's expected return, which can be obtained from financial models or analyst forecasts. We then use this expected return, along with the risk-free rate and standard deviation, to calculate the Sharpe Ratio. This method is useful when we don't have access to historical data or when we want to forecast the investment's future performance.

For example, let's say we want to calculate the Sharpe Ratio of a mutual fund using its expected return. We obtain the expected return from a financial model, which is 12%. We also obtain the standard deviation of the fund's returns, which is 18%. The risk-free rate is 2%. Using the Sharpe Ratio formula, we get: (0.12 - 0.02) / 0.18 = 0.56. This means that the mutual fund is expected to generate a Sharpe Ratio of 0.56, indicating that it is expected to provide a moderate level of excess returns relative to the risk taken.

Limitations of Using Expected Returns

Using expected returns to calculate the Sharpe Ratio has some limitations. Firstly, it relies on estimates, which can be subjective and prone to errors. Secondly, it assumes that the expected return will materialize, which may not always be the case. However, it also has some benefits, such as allowing us to forecast the investment's future performance and providing a more forward-looking perspective.

Method 3: Using a Risk-Free Asset

The third method of calculating the Sharpe Ratio involves using a risk-free asset. This method requires us to have access to a risk-free asset, such as a U.S. Treasury bond, and its return. We then use this return as the risk-free rate in the Sharpe Ratio formula. This method is useful when we want to compare the performance of different investments relative to a risk-free asset.

For example, let's say we want to calculate the Sharpe Ratio of a stock using a U.S. Treasury bond as the risk-free asset. We obtain the return of the Treasury bond, which is 2%. We also obtain the average return and standard deviation of the stock's returns, which are 10% and 15%, respectively. Using the Sharpe Ratio formula, we get: (0.10 - 0.02) / 0.15 = 0.53. This means that the stock has generated a Sharpe Ratio of 0.53, indicating that it has provided a moderate level of excess returns relative to the risk taken.

Benefits of Using a Risk-Free Asset

Using a risk-free asset to calculate the Sharpe Ratio has several benefits. Firstly, it provides a benchmark for evaluating the performance of different investments. Secondly, it allows us to compare the performance of investments with different risk profiles. However, it also has some limitations, such as the potential for interest rate changes and the assumption that the risk-free rate will remain constant.

Method 4: Using a Monte Carlo Simulation

The fourth method of calculating the Sharpe Ratio involves using a Monte Carlo simulation. This method requires us to have access to a financial model and simulation software. We then run multiple simulations of the investment's returns, using different scenarios and assumptions. The resulting Sharpe Ratio is the average of the simulated Sharpe Ratios.

For example, let's say we want to calculate the Sharpe Ratio of a portfolio using a Monte Carlo simulation. We run 1000 simulations of the portfolio's returns, using different scenarios and assumptions. The resulting Sharpe Ratio is the average of the simulated Sharpe Ratios, which is 0.60. This means that the portfolio is expected to generate a Sharpe Ratio of 0.60, indicating that it is expected to provide a moderate level of excess returns relative to the risk taken.

Benefits of Using a Monte Carlo Simulation

Using a Monte Carlo simulation to calculate the Sharpe Ratio has several benefits. Firstly, it allows us to model complex scenarios and assumptions. Secondly, it provides a more comprehensive picture of the investment's performance, taking into account different possible outcomes. However, it also has some limitations, such as the potential for model risk and the assumption that the simulated scenarios will materialize.

Method 5: Using a Spreadsheet

The fifth method of calculating the Sharpe Ratio involves using a spreadsheet. This method requires us to have access to a spreadsheet software, such as Excel, and the necessary formulas and functions. We then input the investment's returns, risk-free rate, and standard deviation into the spreadsheet, and calculate the Sharpe Ratio using the formula.

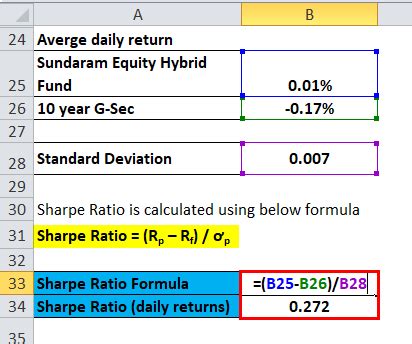
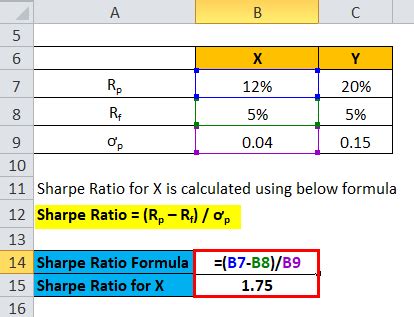
For example, let's say we want to calculate the Sharpe Ratio of a stock using a spreadsheet. We input the stock's returns, risk-free rate, and standard deviation into the spreadsheet, and calculate the Sharpe Ratio using the formula. The resulting Sharpe Ratio is 0.55, indicating that the stock has provided a moderate level of excess returns relative to the risk taken.

Benefits of Using a Spreadsheet

Using a spreadsheet to calculate the Sharpe Ratio has several benefits. Firstly, it provides a simple and intuitive way to calculate the Sharpe Ratio. Secondly, it allows us to easily update and modify the inputs and assumptions. However, it also has some limitations, such as the potential for errors and the assumption that the inputs and assumptions are accurate.

Sharpe Ratio Image Gallery

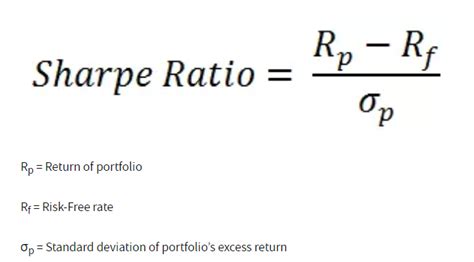
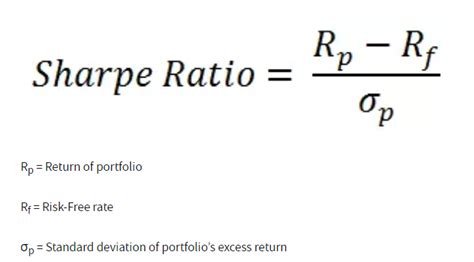
What is the Sharpe Ratio?

The Sharpe Ratio is a financial metric that measures the excess return of an investment over the risk-free rate, relative to its volatility.

How is the Sharpe Ratio calculated?

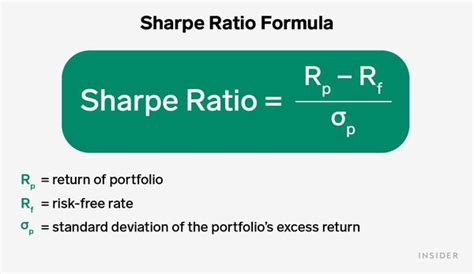
The Sharpe Ratio is calculated by subtracting the risk-free rate from the expected return of an investment and then dividing the result by the standard deviation of the investment's returns.

What are the benefits of using the Sharpe Ratio?

The Sharpe Ratio provides a simple and intuitive way to evaluate the performance of an investment, taking into account both the returns and the risks involved.

What are the limitations of using the Sharpe Ratio?

The Sharpe Ratio has several limitations, including the potential for data biases, the assumption that past performance will continue in the future, and the reliance on estimates and assumptions.

How can I use the Sharpe Ratio in my investment decisions?

The Sharpe Ratio can be used to evaluate the performance of different investments, compare the performance of investments with different risk profiles, and make informed investment decisions.

In conclusion, the Sharpe Ratio is a powerful tool for evaluating the performance of investments, taking into account both the returns and the risks involved. By understanding the different methods of calculating the Sharpe Ratio, investors can make more informed decisions and achieve their financial goals. We encourage readers to share their thoughts and experiences with the Sharpe Ratio, and to explore the different methods of calculating it. Whether you are a seasoned investor or just starting out, the Sharpe Ratio is an essential metric to understand and use in your investment decisions.