Intro
Understanding the concept of p-value and its significance in statistical analysis is crucial for making informed decisions based on data. The p-value, or probability value, is a key concept in hypothesis testing, indicating the probability of observing results at least as extreme as those observed, assuming that the null hypothesis is true. In the context of a t-test, which is used to compare the means of two groups, the p-value helps determine whether the difference between the groups is statistically significant. Excel, being a powerful tool for data analysis, provides several methods to calculate the p-value from a t-test. Here, we'll delve into the importance of p-values, the basics of t-tests, and how to calculate p-values from t-tests in Excel.
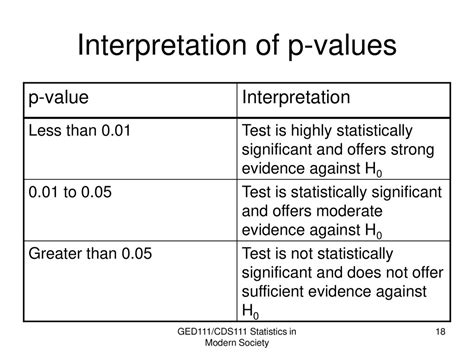
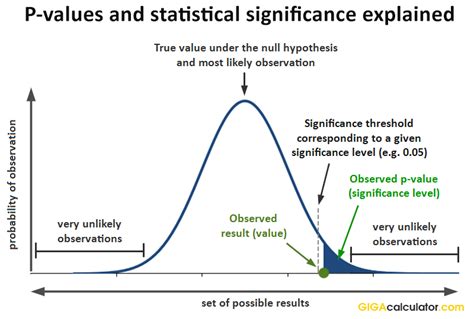
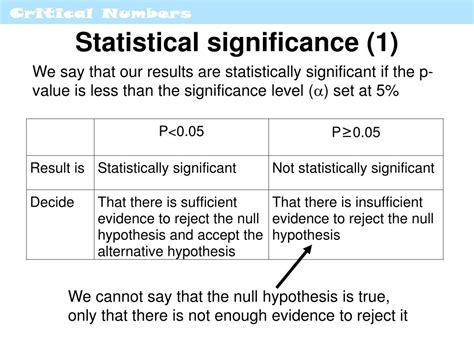
The p-value is a pivotal element in statistical hypothesis testing, serving as an indicator of whether the results of an experiment or study are due to chance or if they reflect a real effect. A small p-value (typically less than 0.05) indicates that the observed data would be very unlikely under the null hypothesis, leading to the rejection of the null hypothesis in favor of the alternative hypothesis. This threshold of 0.05 is commonly used, although it can vary depending on the field of study or the specific requirements of the analysis.
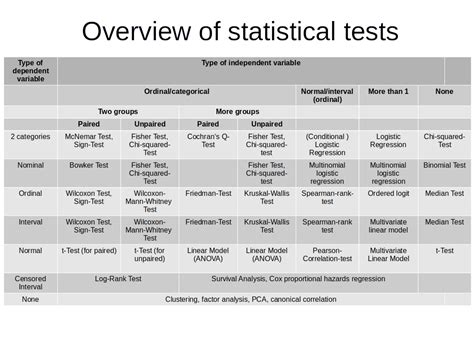
T-tests are a type of statistical test used to compare the means of two groups to see if there is a significant difference between them. They are commonly used in a variety of fields, including business, medicine, and social sciences. The two main types of t-tests are the independent samples t-test (comparing means from two separate groups) and the paired samples t-test (comparing means from the same group at different times or under different conditions).
To calculate the p-value from a t-test in Excel, you can use the built-in functions such as T.TEST or T.TEST.2T (for two-tailed tests). The T.TEST function returns the probability that the observed difference between the sample means occurred by chance, which is the p-value. The syntax for the T.TEST function is T.TEST(array1, array2, tails, type), where array1 and array2 are the ranges of the two datasets, tails specifies whether the test is one-tailed or two-tailed, and type specifies the type of t-test (1 for paired, 2 for two-sample equal variance, and 3 for two-sample unequal variance).
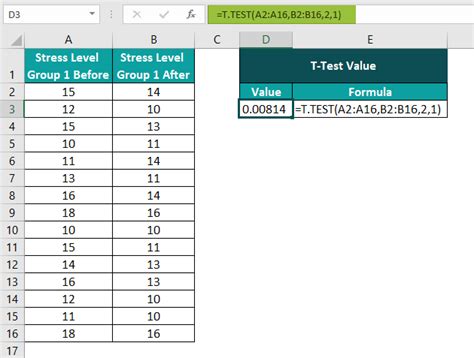
For example, if you have two datasets in columns A and B of your Excel sheet, and you want to perform a two-tailed independent samples t-test assuming equal variances, you would use the formula =T.TEST(A1:A10, B1:B10, 2, 2). This formula calculates the p-value based on the data in cells A1 through A10 and B1 through B10, using a two-tailed test (specifying that the difference could be in either direction) and assuming that the two datasets have equal variances.
Understanding T-Test Types

When conducting a t-test, it's crucial to choose the correct type based on the research design and the nature of the data. The three main types of t-tests are the independent samples t-test, the paired samples t-test, and the one-sample t-test. Each serves a different purpose: comparing the means of two independent groups, comparing the means of related groups, or comparing a sample mean to a known population mean, respectively.
Independent Samples T-Test
This test is used to compare the means of two independent groups. For instance, if you want to compare the average scores of students from two different schools, you would use an independent samples t-test. The key assumption here is that the observations in each group are independent of the observations in the other group.

Paired Samples T-Test
The paired samples t-test, on the other hand, is used when the observations in the two groups are paired in some way. A classic example is a before-and-after study, where measurements are taken from the same subjects under two different conditions. This test is particularly useful for assessing the impact of an intervention or change.

Calculating P-Value in Excel
Calculating the p-value in Excel can be straightforward using the T.TEST function, as mentioned earlier. However, understanding what the p-value represents is just as important as calculating it. The p-value gives you the probability of observing your results (or more extreme) if the null hypothesis were true. If this probability is below your chosen significance level (often 0.05), you reject the null hypothesis, suggesting that the observed difference is statistically significant.

Interpreting P-Values
Interpreting p-values correctly is crucial for drawing accurate conclusions from your data. A p-value of 0.05 or less typically indicates statistical significance, meaning that the observed effect is unlikely to be due to chance. However, it does not provide information on the size or importance of the effect. For this, you might also consider calculating the effect size.
Common Mistakes in T-Tests and P-Value Interpretation
When conducting t-tests and interpreting p-values, there are several common mistakes to watch out for. These include misunderstanding the null and alternative hypotheses, failing to check the assumptions of the t-test (such as normality and equal variances), and misinterpreting the p-value as the probability that the null hypothesis is true.

Assumptions of T-Tests
T-tests assume that the data follows a normal distribution and that the variances of the two groups are equal (for the independent samples t-test with equal variances assumed). Violating these assumptions can lead to inaccurate results. There are methods to check these assumptions, such as the Shapiro-Wilk test for normality and the F-test for equality of variances.

Gallery of T-Test and P-Value Related Images
T-Test and P-Value Image Gallery






Frequently Asked Questions
What is the purpose of a t-test?
+The t-test is used to compare the means of two groups to determine if there is a significant difference between them.
How do I calculate the p-value in Excel?
+You can calculate the p-value in Excel using the T.TEST function, which returns the probability that the observed difference between the sample means occurred by chance.
What does a p-value of 0.05 indicate?
+A p-value of 0.05 or less typically indicates statistical significance, meaning that the observed effect is unlikely to be due to chance.
To sum up, understanding and correctly applying t-tests, along with interpreting their p-values, is essential for statistical analysis. By following the guidelines and tips outlined above, and being mindful of the common pitfalls, you can effectively use Excel to perform t-tests and make informed decisions based on your data. Whether you're a researcher, student, or professional, mastering these skills will enhance your ability to analyze and interpret data, leading to more accurate conclusions and better decision-making. We encourage you to share your experiences with t-tests and p-value interpretation, and to ask any further questions you may have in the comments below.