Intro
Discover 5 ways to apply the Mann Whitney test, a non-parametric statistical method, for comparing two independent samples and analyzing ordinal data, using Wilcoxon rank-sum and median differences.
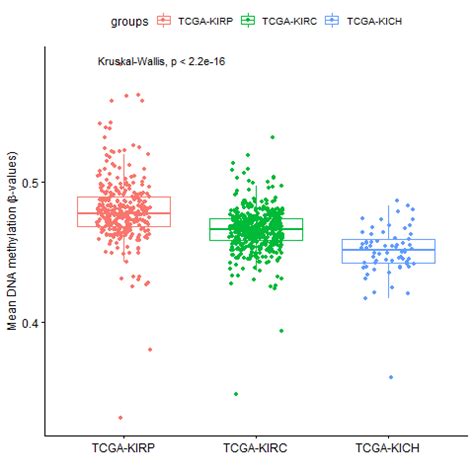
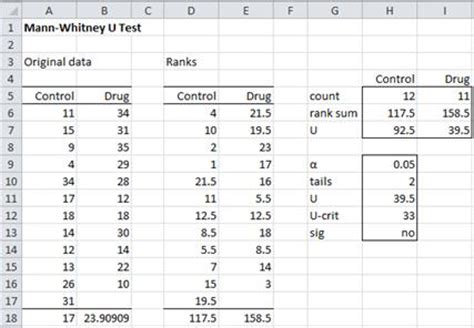
The Mann-Whitney test, also known as the Wilcoxon rank-sum test, is a non-parametric statistical test used to compare two independent samples. It is a powerful tool for analyzing continuous data that does not meet the assumptions of parametric tests, such as normality or equal variances. In this article, we will explore five ways to apply the Mann-Whitney test in real-world scenarios.
Introduction to the Mann-Whitney Test
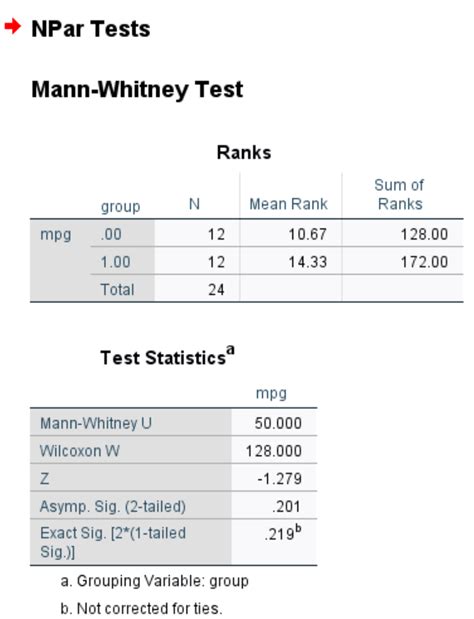
Methodology of the Mann-Whitney Test
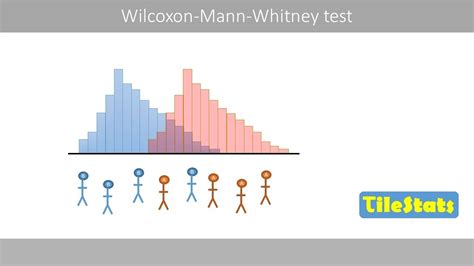
Interpreting the Results of the Mann-Whitney Test

Common Applications of the Mann-Whitney Test

Limitations and Assumptions of the Mann-Whitney Test
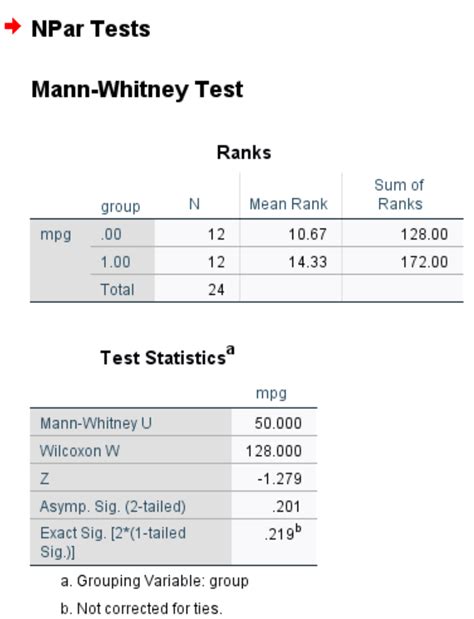
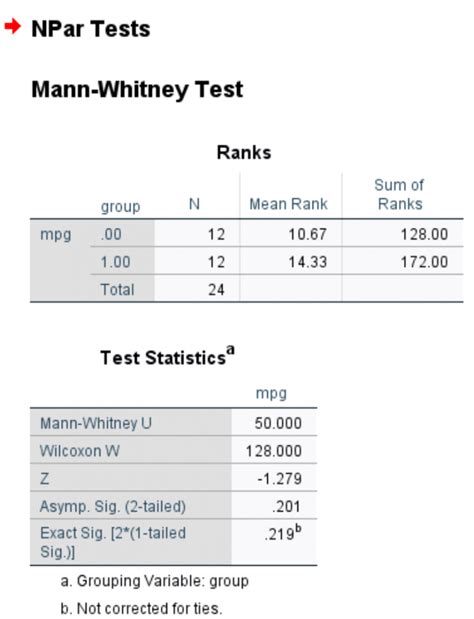
Gallery of Mann Whitney Test
Mann Whitney Test Image Gallery

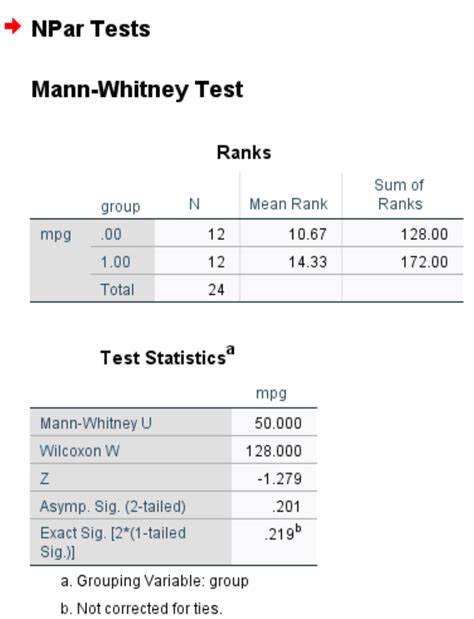
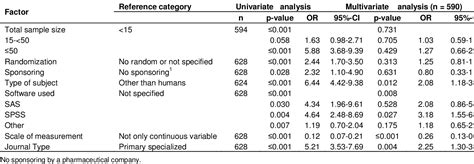
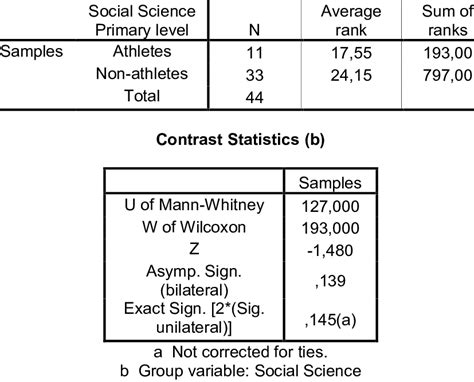


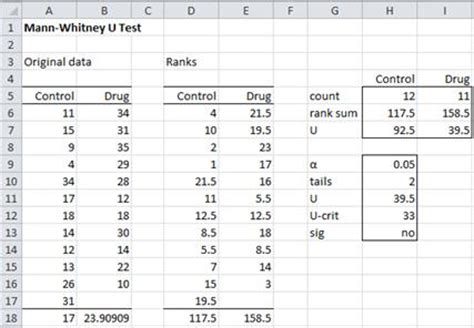
What is the Mann-Whitney test used for?
+The Mann-Whitney test is used to compare two independent samples and determine if there is a significant difference between them.
What are the assumptions of the Mann-Whitney test?
+The Mann-Whitney test assumes that the data is independent and identically distributed, and that the samples are randomly selected.
How do I interpret the results of the Mann-Whitney test?
+The results of the Mann-Whitney test are typically reported as a p-value, which indicates the probability of observing the test statistic under the null hypothesis. If the p-value is less than a certain significance level (usually 0.05), the null hypothesis is rejected, and it is concluded that the two samples come from different distributions.
What are some common applications of the Mann-Whitney test?
+The Mann-Whitney test has a wide range of applications in fields such as medicine, social sciences, and engineering. It can be used to compare the effectiveness of different treatments, the attitudes of different groups, or the performance of different machines.
What are some limitations of the Mann-Whitney test?
+While the Mann-Whitney test is a powerful tool, it has some limitations. For example, the test assumes that the data is independent and identically distributed, and that the samples are randomly selected. Additionally, the test can be sensitive to outliers and may not perform well with small sample sizes.
We hope this article has provided you with a comprehensive understanding of the Mann-Whitney test and its applications. Whether you are a student, researcher, or practitioner, this test is a valuable tool for comparing two independent samples and determining if there is a significant difference between them. If you have any questions or comments, please do not hesitate to reach out. Share this article with your colleagues and friends who may be interested in learning more about the Mann-Whitney test.