5 Excel Covariance Tips

Understanding the relationship between different variables in a dataset is crucial for making informed decisions in various fields, including finance, economics, and social sciences. One statistical measure that helps in analyzing this relationship is covariance. In Microsoft Excel, calculating covariance is straightforward, and there are several tips and tricks to get the most out of this functionality. This article will delve into the world of Excel covariance, providing tips and insights on how to effectively use this statistical tool.

Covariance measures how much two variables change together. If the covariance is positive, it means that when one variable increases, the other variable also tends to increase. A negative covariance indicates that when one variable increases, the other decreases. This concept is fundamental in understanding the correlation between different sets of data, which is essential for forecasting, risk analysis, and portfolio management. Excel, being a powerful tool for data analysis, offers several functions to calculate covariance, including the COVAR, COVARIANCE.P, and COVARIANCE.S functions.

Understanding Covariance in Excel

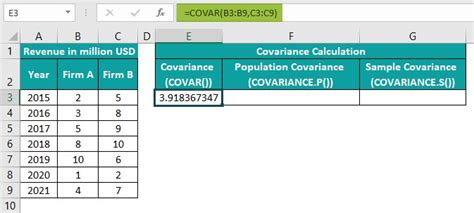
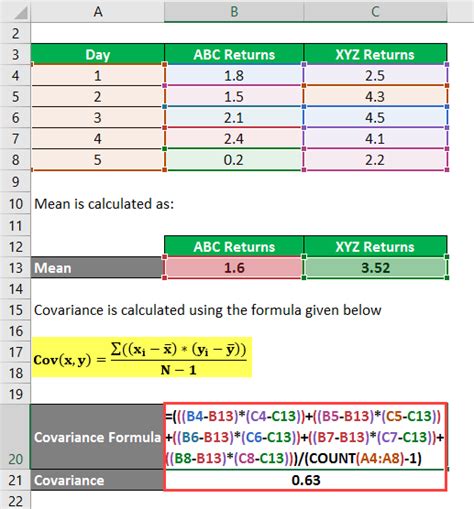
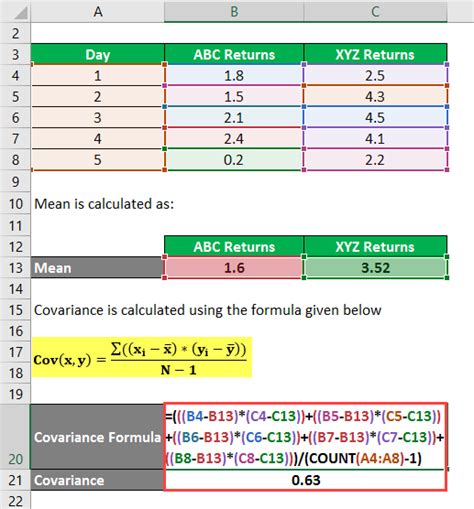
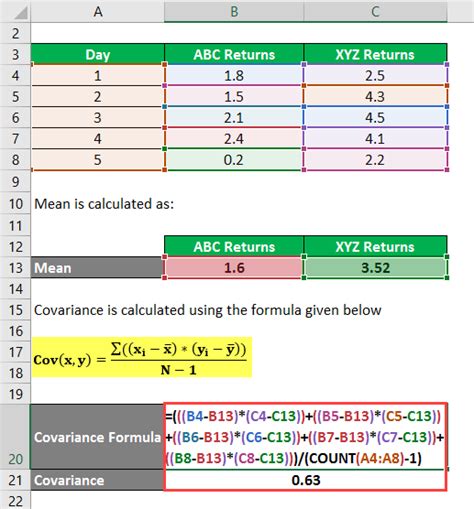
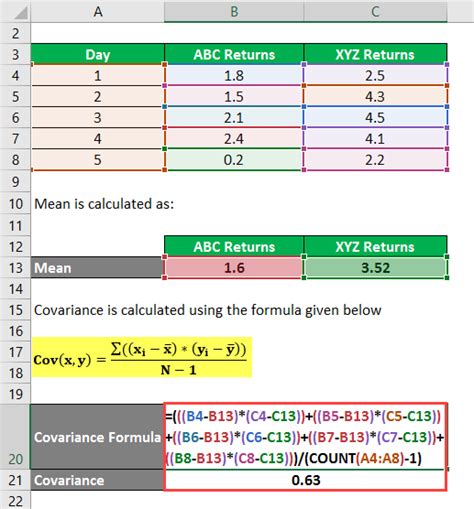
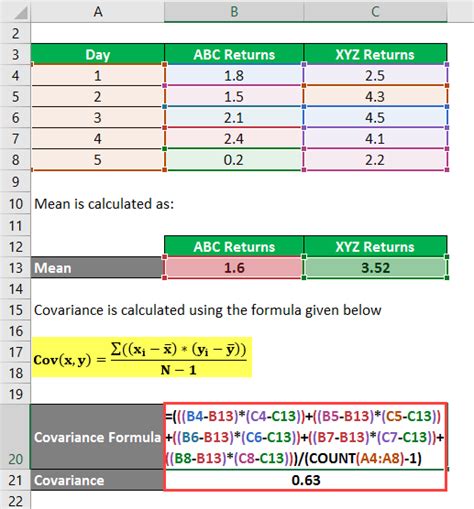
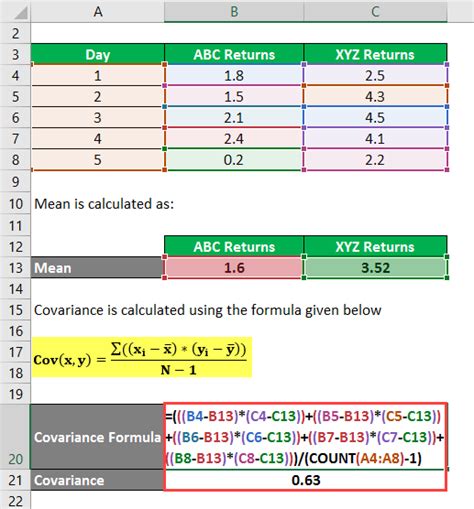
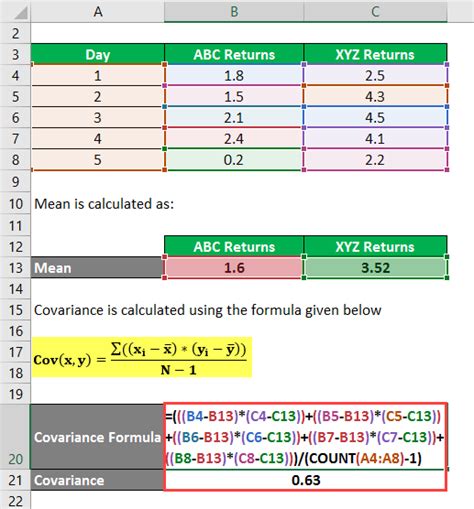
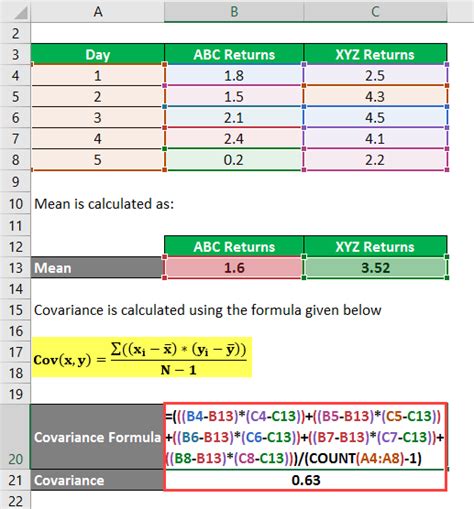
To begin with, it's essential to understand the difference between the various covariance functions available in Excel. The COVAR function calculates the covariance between two sets of data points, which can be used to understand how changes in one variable correspond to changes in another. This function is straightforward to use, requiring only the arrays of data as input. For example, if you have two sets of data in columns A and B, the formula to calculate the covariance would be =COVAR(A1:A10, B1:B10), assuming the data points are from cell A1 to A10 and B1 to B10.

Calculating Covariance with COVARIANCE.P and COVARIANCE.S

In addition to the COVAR function, Excel provides the COVARIANCE.P and COVARIANCE.S functions for calculating the population and sample covariance, respectively. The COVARIANCE.P function is used when the data represents the entire population, while the COVARIANCE.S function is used for sample data, where the data is a subset of the population. Understanding which function to use depends on the nature of the data and the analysis goals. For instance, if you are analyzing the entire dataset of a company's stock prices over a year, you would use COVARIANCE.P. However, if you are analyzing a sample of stock prices from a larger set, COVARIANCE.S would be more appropriate.

Benefits of Using Covariance in Data Analysis

The benefits of using covariance in data analysis are numerous:

Risk Management: By understanding how different assets move together, investors can diversify their portfolios to minimize risk.
Forecasting: Covariance can help in predicting future trends by analyzing past relationships between variables.
Decision Making: It provides valuable insights into how changes in one variable might affect another, which is crucial for strategic decision-making.

Practical Applications of Covariance

Covariance has practical applications across various sectors:

Finance: It's used in portfolio management to assess the risk associated with different asset combinations.
Economics: Economists use covariance to study the relationship between economic indicators, such as GDP and inflation rates.
Social Sciences: Researchers might use covariance to analyze the relationship between different social factors, like education level and income.

Steps to Calculate Covariance in Excel

Calculating covariance in Excel involves the following steps:

Prepare Your Data: Ensure your data is organized in columns or rows.
Choose the Function: Decide whether to use COVAR, COVARIANCE.P, or COVARIANCE.S based on your data.
Apply the Formula: Input the formula with the correct arrays.
Interpret Results: Understand the implications of the covariance value for your analysis.

Common Mistakes to Avoid

When working with covariance in Excel, it's essential to avoid common mistakes:

Incorrect Function Usage: Using COVARIANCE.P for sample data or vice versa can lead to incorrect conclusions.
Data Errors: Ensure data is accurate and free of errors, as covariance calculations are sensitive to data quality.
Misinterpretation: Failing to understand the implications of covariance values can lead to incorrect decisions.

Best Practices for Covariance Analysis

Best practices for covariance analysis include:

Data Validation: Always validate your data before analysis.
Function Selection: Carefully select the appropriate covariance function.
Result Interpretation: Take the time to understand what the covariance results mean for your specific context.

Advanced Covariance Analysis

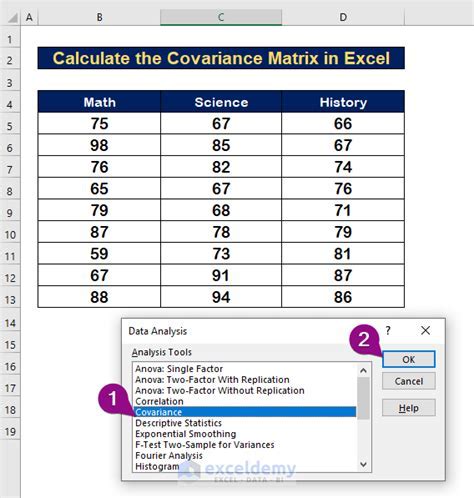
For advanced users, Excel offers the capability to perform more complex covariance analyses, including:

Multivariate Analysis: Analyzing the covariance between more than two variables.
Correlation Analysis: Using covariance to calculate correlation coefficients, which provide a standardized measure of the relationship between variables.

Tools and Resources for Further Learning

For those looking to deepen their understanding of covariance and its applications in Excel, several tools and resources are available:

Excel Documentation: Microsoft provides extensive documentation on Excel functions, including covariance calculations.
Online Courses: Websites like Coursera, edX, and Udemy offer courses on data analysis and statistics that cover covariance.
Professional Communities: Joining professional communities, like the Excel subreddit or data analysis forums, can provide access to expert advice and real-world examples.

Gallery of Covariance Examples

Covariance Image Gallery

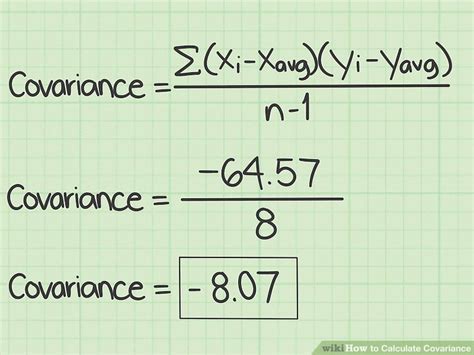
Frequently Asked Questions

What is the difference between COVARIANCE.P and COVARIANCE.S?

COVARIANCE.P is used for population data, while COVARIANCE.S is used for sample data. The main difference lies in how they calculate the covariance, with COVARIANCE.S providing a more conservative estimate by dividing by n-1 instead of n.

How do I interpret covariance values?

A positive covariance indicates that the variables tend to increase together, a negative covariance indicates they tend to move in opposite directions, and a covariance close to zero suggests no linear relationship. The magnitude of the covariance value indicates the strength of the relationship but depends on the scale of the variables.

Can I use covariance for forecasting?

Yes, covariance can be used as part of forecasting models to understand how variables move together over time. However, it's essential to consider other statistical measures and possibly more advanced models for accurate predictions.

In conclusion, mastering the use of covariance in Excel can significantly enhance data analysis capabilities, providing valuable insights into the relationships between different variables. By understanding the basics of covariance, selecting the appropriate function, and avoiding common pitfalls, users can leverage this powerful statistical tool to make more informed decisions. Whether in finance, economics, or social sciences, the applications of covariance are vast, and with practice, individuals can become proficient in using Excel to uncover the hidden patterns in their data. We invite you to share your experiences with covariance analysis in Excel, ask questions, or explore further resources to deepen your understanding of this essential statistical concept.