Intro
Understanding how to multiply negatives is a fundamental concept in mathematics, essential for various calculations and problem-solving exercises. The concept may seem straightforward, but it's crucial to grasp the underlying principles to avoid confusion. Multiplying negatives involves understanding the rules of signs, which dictate how positive and negative numbers interact during multiplication. In this article, we'll delve into the world of negative numbers, exploring the rules and applications of multiplying negatives, along with practical examples to solidify your understanding.
Multiplying negatives is not just about following a set of rules; it's also about understanding the conceptual framework behind these operations. When you multiply two negative numbers, the result is always positive. This is because the multiplication of two negative numbers cancels out their negative signs, resulting in a positive product. On the other hand, when you multiply a negative number by a positive number, the result is always negative, as the negative sign dominates the operation.
To further illustrate this concept, let's consider some basic examples. If you multiply -2 by -3, the result is 6, which is positive. However, if you multiply -2 by 3, the result is -6, which is negative. These simple examples demonstrate the fundamental principle of multiplying negatives: two negatives make a positive, and a negative and a positive make a negative.
Understanding the Basics of Multiplying Negatives
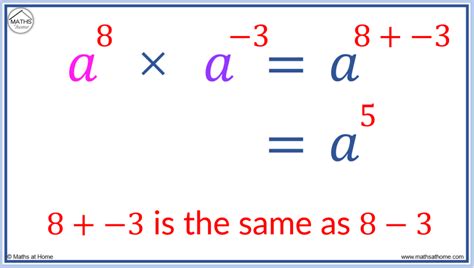
Understanding the basics of multiplying negatives is crucial for advancing in mathematics. It's a concept that appears in various mathematical operations, from simple arithmetic to complex algebraic expressions. The rule is simple: when multiplying two numbers, if both are negative, the result is positive. If one is negative and the other is positive, the result is negative. This rule applies universally, regardless of the numbers involved.
Applying the Rule in Different Scenarios
The application of this rule can be seen in different mathematical scenarios. For instance, in algebra, when solving equations or simplifying expressions, understanding how to multiply negatives is essential. It helps in simplifying complex expressions and solving equations accurately. Moreover, in real-world applications, such as finance, physics, and engineering, the concept of multiplying negatives plays a critical role in calculations involving negative quantities or directions.Practical Examples of Multiplying Negatives

Let's consider some practical examples to illustrate the concept further. For instance, if you have a debt of $100 (represented as -100) and you multiply this by -2 (representing a reversal of the debt), the result is $200, indicating that the debt has not only been cleared but you also have $200 in your favor. This example demonstrates how multiplying two negative numbers results in a positive outcome.
In contrast, if you have a savings of $100 (represented as +100) and you multiply this by -2 (representing a withdrawal or loss), the result is -200, indicating a loss or debt of $200. This shows how multiplying a positive by a negative results in a negative outcome.
Real-World Applications
The concept of multiplying negatives has numerous real-world applications. In physics, for example, direction is often represented by positive or negative signs. When calculating distances or velocities in opposite directions, understanding how to multiply negatives is crucial for obtaining the correct results. Similarly, in finance, transactions involving debts or credits require a clear understanding of how negative numbers interact during multiplication.Steps to Multiply Negatives

Multiplying negatives involves a straightforward process:
- Identify the Signs: Determine the signs of the numbers you are multiplying. Are they both negative, both positive, or one of each?
- Apply the Rule: If both numbers are negative, the result will be positive. If one is negative and the other is positive, the result will be negative.
- Multiply the Numbers: Ignore the signs for a moment and multiply the numbers as you normally would.
- Apply the Sign: Based on the rule, apply the appropriate sign to your result.
Common Mistakes to Avoid
One of the common mistakes when multiplying negatives is forgetting to apply the rule correctly. It's essential to double-check the signs of the numbers and the result to ensure accuracy. Another mistake is confusing the rule with the rules for addition and subtraction, which deal with signs differently.Benefits of Understanding Multiplying Negatives

Understanding how to multiply negatives offers several benefits:
- Improved Mathematical Skills: Grasping this concept enhances your overall mathematical proficiency, making it easier to tackle more complex problems.
- Accuracy in Calculations: Knowing the rules of multiplying negatives ensures accuracy in your calculations, which is crucial in various fields like science, engineering, and finance.
- Problem-Solving Abilities: It improves your ability to solve problems that involve negative numbers, which is essential for real-world applications.
Enhancing Your Understanding
To further enhance your understanding of multiplying negatives, practice is key. Engage in exercises that involve multiplying negative numbers in different scenarios. This will not only solidify your grasp of the concept but also improve your speed and accuracy in performing these operations.Conclusion and Next Steps

In conclusion, multiplying negatives is a fundamental mathematical concept that plays a critical role in various calculations and problem-solving exercises. By understanding the rules and applying them correctly, you can enhance your mathematical skills, improve your accuracy in calculations, and develop your problem-solving abilities. Remember, practice is essential for mastering this concept, so engage in as many exercises as you can to solidify your understanding.
Final Thoughts
As you continue to explore the world of mathematics, keep in mind that concepts like multiplying negatives are not just abstract rules but have real-world implications. They are essential for making sense of the world around us, from understanding financial transactions to calculating distances in space. By embracing these concepts and practicing them regularly, you'll find that mathematics becomes not just a subject in school but a powerful tool for understanding and navigating the world.Multiplying Negatives Image Gallery










What is the rule for multiplying two negative numbers?
+When you multiply two negative numbers, the result is always positive.
How does the sign of the result change when multiplying a negative and a positive number?
+The result is always negative when multiplying a negative and a positive number.
What are some real-world applications of multiplying negatives?
+Multiplying negatives has applications in finance, physics, and engineering, among other fields, where negative quantities or directions are involved.
We hope this article has provided you with a comprehensive understanding of multiplying negatives. Whether you're a student looking to improve your mathematical skills or a professional seeking to apply these concepts in real-world scenarios, the ability to multiply negatives accurately is indispensable. Share your thoughts on this topic, and let's continue the conversation on the importance of mathematical concepts in our daily lives.