Intro
The concept of Newey West standard errors is crucial in the field of econometrics, particularly when dealing with time series data. This method is designed to address issues related to heteroscedasticity and autocorrelation in the residuals of a regression model, which can lead to inaccurate estimates of standard errors and, consequently, affect hypothesis testing and confidence intervals.
The importance of accurate standard error estimation cannot be overstated. Standard errors are fundamental in understanding the variability of estimates and making inferences about the population parameters. When standard errors are underestimated, it can lead to Type I errors, where the null hypothesis is rejected incorrectly, while overestimation can result in Type II errors, failing to reject a false null hypothesis. Therefore, methods like Newey West that provide more robust standard error estimates are invaluable in econometric analysis.
Econometricians and researchers often encounter challenges when analyzing time series data due to its inherent characteristics, such as trends, seasonal patterns, and potential non-stationarity. These characteristics can complicate the analysis, especially when the assumption of independent and identically distributed (i.i.d.) errors is violated. The Newey West procedure is a significant advancement in addressing these challenges by providing a way to adjust standard errors for serial correlation and heteroscedasticity, thereby ensuring more reliable statistical inferences.
Introduction to Newey West Standard Errors

The Newey West standard errors method, developed by Whitney Newey and Kenneth West, is an extension of the White standard errors technique, which corrects for heteroscedasticity. The Newey West approach further accounts for autocorrelation by using a kernel function to weight the autocovariances of the residuals. This weighting scheme diminishes as the lag between observations increases, effectively capturing the impact of autocorrelation on standard error estimates.
Working Mechanism of Newey West Standard Errors
The mechanism behind Newey West standard errors involves several key steps: - Estimation of the regression model to obtain residuals. - Calculation of the autocovariances of the residuals up to a certain lag. - Application of a kernel (or weighting) function to these autocovariances to adjust for autocorrelation. - Computation of the variance-covariance matrix of the coefficients using the adjusted autocovariances. - Derivation of the Newey West standard errors from the diagonal elements of this variance-covariance matrix.Benefits and Applications
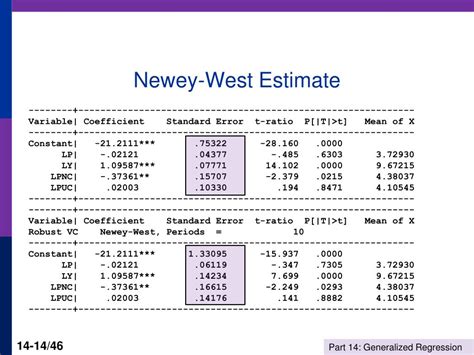
The Newey West standard errors offer several benefits, including:
- Robustness to Heteroscedasticity and Autocorrelation: By accounting for both heteroscedasticity and autocorrelation, these standard errors provide a more accurate basis for statistical inference.
- Flexibility: The method can be applied to a wide range of regression models, including linear and nonlinear models.
- Improved Hypothesis Testing: With more accurate standard error estimates, hypothesis testing becomes more reliable, reducing the likelihood of incorrect inferences.
Steps for Implementing Newey West Standard Errors
Implementing Newey West standard errors involves the following steps: 1. **Model Estimation**: Estimate the regression model using ordinary least squares (OLS) or another suitable method. 2. **Residual Calculation**: Calculate the residuals from the estimated model. 3. **Autocovariance Calculation**: Compute the autocovariances of the residuals up to a specified lag. 4. **Kernel Application**: Apply a kernel function to the autocovariances to adjust for autocorrelation. 5. **Variance-Covariance Matrix Calculation**: Calculate the variance-covariance matrix of the coefficients using the adjusted autocovariances. 6. **Standard Error Calculation**: Derive the Newey West standard errors from the diagonal elements of the variance-covariance matrix.Practical Examples and Statistical Data
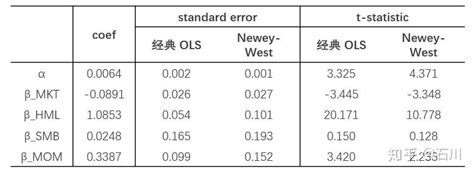
To illustrate the application of Newey West standard errors, consider a study analyzing the relationship between economic growth (GDP) and investment in a country over several years. The data may exhibit heteroscedasticity due to varying economic conditions and autocorrelation because of the time series nature of the data. By applying the Newey West method, researchers can obtain more reliable standard errors for the coefficients, leading to more accurate conclusions about the relationship between economic growth and investment.
Common Challenges and Limitations
While the Newey West standard errors method is powerful, it is not without challenges and limitations: - **Choice of Lag**: The choice of the maximum lag for calculating autocovariances can significantly affect the results. Too few lags may not fully capture autocorrelation, while too many can introduce unnecessary noise. - **Kernel Selection**: The choice of kernel function can also influence the estimates. Different kernels may perform better under different circumstances, and there is no one-size-fits-all solution.Gallery of Newey West Standard Errors
Newey West Standard Errors Image Gallery








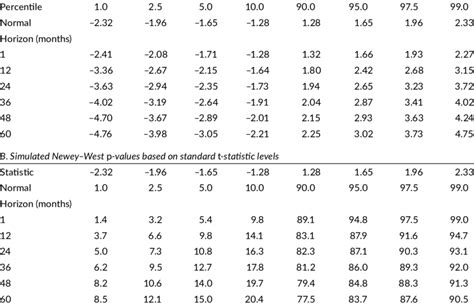

Frequently Asked Questions
What are Newey West standard errors?
+Newey West standard errors are a method used in econometrics to adjust standard errors for serial correlation and heteroscedasticity in regression models.
Why are Newey West standard errors important?
+They provide more accurate estimates of standard errors, which is crucial for reliable hypothesis testing and confidence intervals in the presence of heteroscedasticity and autocorrelation.
How do I choose the lag for Newey West standard errors?
+The choice of lag depends on the data and the model. Common practices include using a rule of thumb, such as the Newey West automatic lag selection, or selecting a lag based on the autocorrelation function of the residuals.
In conclusion, the Newey West standard errors method is a valuable tool for econometricians and researchers dealing with time series data. By accounting for both heteroscedasticity and autocorrelation, it provides more robust standard error estimates, leading to more reliable statistical inferences. As with any statistical method, understanding its application, benefits, and limitations is crucial for effective use. We invite readers to share their experiences and questions regarding the application of Newey West standard errors in their research and to explore further the nuances of this important econometric technique.