Intro
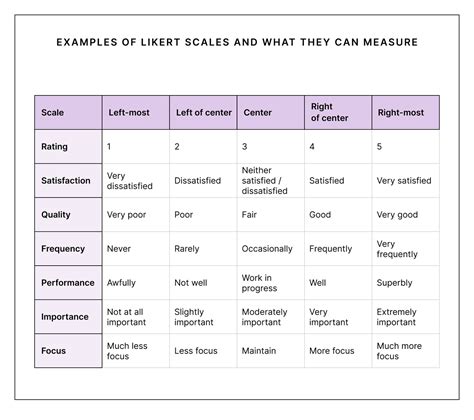
Discover the Scale Range Change Formula, a crucial concept in data analysis, involving ratio scale, interval scale, and ordinal scale transformations, to accurately measure and interpret data, ensuring reliable results and informed decision-making.
The concept of scale range change is crucial in various fields, including music, geography, and data analysis. Understanding how to calculate and apply scale range changes is essential for professionals and enthusiasts alike. In this article, we will delve into the world of scale range changes, exploring the formula, its applications, and providing examples to illustrate its usage.
Scale range change refers to the process of adjusting the range of values or measurements to a new scale, while maintaining the relative proportions between the data points. This is often necessary when working with different units of measurement, comparing data from various sources, or visualizing data on a specific scale. The scale range change formula is a mathematical expression that enables us to perform these adjustments accurately.
To begin with, it is essential to understand the importance of scale range changes in different contexts. In music, for instance, changing the scale range of a melody can alter its mood and character. In geography, scale range changes are used to create maps with varying levels of detail, allowing users to navigate and understand spatial relationships more effectively. In data analysis, scale range changes help to reveal patterns and trends that may not be apparent when using the original scale.
The scale range change formula is relatively straightforward and can be applied to various types of data. The basic formula is:
New Value = (Old Value - Old Minimum) / (Old Maximum - Old Minimum) * (New Maximum - New Minimum) + New Minimum
This formula takes into account the original minimum and maximum values, as well as the desired new minimum and maximum values. By applying this formula, we can transform the original data to the new scale, preserving the relative relationships between the data points.
To illustrate the application of the scale range change formula, let's consider a simple example. Suppose we have a set of exam scores ranging from 0 to 100, and we want to convert them to a new scale with a range of 0 to 10. Using the formula, we can calculate the new score for each student.
For instance, if a student scored 80 on the original scale, we would apply the formula as follows:
New Score = (80 - 0) / (100 - 0) * (10 - 0) + 0 New Score = 80 / 100 * 10 New Score = 8
Therefore, the student's new score on the 0-10 scale would be 8.
Applications of Scale Range Change
The scale range change formula has numerous applications in various fields, including:
- Music: Changing the scale range of a melody or harmony can alter its mood and character.
- Geography: Scale range changes are used to create maps with varying levels of detail, allowing users to navigate and understand spatial relationships more effectively.
- Data Analysis: Scale range changes help to reveal patterns and trends that may not be apparent when using the original scale.
- Engineering: Scale range changes are used to convert between different units of measurement, such as converting temperature from Celsius to Fahrenheit.
Benefits of Scale Range Change
The scale range change formula offers several benefits, including:
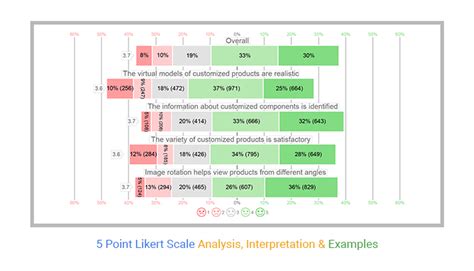
- Improved data visualization: By adjusting the scale range, we can create more informative and engaging visualizations that reveal patterns and trends in the data.
- Enhanced comparison: Scale range changes enable us to compare data from different sources or with different units of measurement, facilitating more accurate analysis and decision-making.
- Increased flexibility: The scale range change formula allows us to adapt data to different contexts and applications, making it a valuable tool in various fields.
Steps for Applying the Scale Range Change Formula
To apply the scale range change formula, follow these steps:
- Identify the original minimum and maximum values of the data.
- Determine the desired new minimum and maximum values for the new scale.
- Apply the formula to each data point, using the original and new minimum and maximum values.
- Verify the results to ensure that the relative relationships between the data points have been preserved.

Common Challenges and Limitations
While the scale range change formula is a powerful tool, there are some common challenges and limitations to consider:
- Loss of precision: When converting data to a new scale, some precision may be lost, particularly if the new scale has a smaller range.
- Non-linear relationships: The scale range change formula assumes a linear relationship between the original and new scales. If the relationship is non-linear, the formula may not produce accurate results.
- Outliers and anomalies: The presence of outliers or anomalies in the data can affect the accuracy of the scale range change formula.
Real-World Examples of Scale Range Change
The scale range change formula has numerous real-world applications, including:
- Converting temperature from Celsius to Fahrenheit
- Changing the scale of a map to display more or less detail
- Adjusting the range of a musical instrument to produce different tones and pitches
- Normalizing data for machine learning algorithms
Best Practices for Scale Range Change
To ensure accurate and effective scale range changes, follow these best practices:
- Verify the original and new minimum and maximum values to ensure accuracy.
- Use the formula consistently to maintain relative relationships between data points.
- Consider the potential loss of precision and non-linear relationships when applying the formula.
- Document the scale range change process to facilitate reproducibility and transparency.

Scale Range Change Image Gallery


What is the purpose of the scale range change formula?
+The scale range change formula is used to adjust the range of values or measurements to a new scale, while maintaining the relative proportions between the data points.
How do I apply the scale range change formula?
+To apply the formula, identify the original minimum and maximum values, determine the desired new minimum and maximum values, and apply the formula to each data point.
What are some common challenges and limitations of the scale range change formula?
+Common challenges and limitations include loss of precision, non-linear relationships, and the presence of outliers or anomalies in the data.
Can I use the scale range change formula for non-linear relationships?
+The scale range change formula assumes a linear relationship between the original and new scales. If the relationship is non-linear, the formula may not produce accurate results.
How can I ensure accurate and effective scale range changes?
+To ensure accurate and effective scale range changes, verify the original and new minimum and maximum values, use the formula consistently, and consider the potential loss of precision and non-linear relationships.
In conclusion, the scale range change formula is a powerful tool for adjusting the range of values or measurements to a new scale, while maintaining the relative proportions between the data points. By understanding the formula, its applications, and best practices, professionals and enthusiasts can apply scale range changes effectively in various fields, including music, geography, and data analysis. We invite you to share your experiences and questions about scale range changes in the comments below, and to explore the resources and examples provided in this article to deepen your understanding of this essential concept.