Intro
Matrix equations are a fundamental concept in linear algebra and are used to solve systems of linear equations. In Excel, matrix equations can be solved using various methods, including the built-in functions and add-ins. In this article, we will explore the importance of matrix equations, their applications, and how to solve them in Excel.
Matrix equations have numerous applications in various fields, including physics, engineering, economics, and computer science. They are used to model complex systems, optimize processes, and make predictions. For instance, in physics, matrix equations are used to describe the motion of objects, while in economics, they are used to model the behavior of markets. The ability to solve matrix equations is essential in these fields, and Excel provides a powerful tool for doing so.
The importance of matrix equations cannot be overstated. They provide a compact and efficient way to represent and solve systems of linear equations. In many cases, matrix equations can be used to solve problems that would be difficult or impossible to solve using traditional methods. Furthermore, matrix equations can be used to analyze and visualize complex data, making them a valuable tool for data analysis and interpretation.
Introduction to Matrix Equations
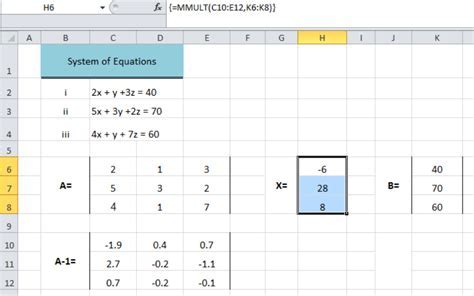
A matrix equation is an equation that involves a matrix, which is a rectangular array of numbers. Matrix equations can be used to represent systems of linear equations, where the unknowns are the elements of the matrix. The general form of a matrix equation is AX = B, where A is the coefficient matrix, X is the variable matrix, and B is the constant matrix.
To solve a matrix equation, we need to find the value of X that satisfies the equation. This can be done using various methods, including inverse matrices, Gaussian elimination, and LU decomposition. In Excel, we can use the built-in functions, such as MINVERSE and MMULT, to solve matrix equations.
Methods for Solving Matrix Equations
There are several methods for solving matrix equations, including:
- Inverse matrices: This method involves finding the inverse of the coefficient matrix A and then multiplying it by the constant matrix B to get the solution.
- Gaussian elimination: This method involves transforming the coefficient matrix A into upper triangular form and then solving for the unknowns.
- LU decomposition: This method involves decomposing the coefficient matrix A into lower and upper triangular matrices and then solving for the unknowns.
Each method has its advantages and disadvantages, and the choice of method depends on the specific problem and the size of the matrix.
Using Inverse Matrices
The inverse matrix method is a popular method for solving matrix equations. It involves finding the inverse of the coefficient matrix A and then multiplying it by the constant matrix B to get the solution. The inverse of a matrix A is denoted by A^(-1) and is defined as the matrix that satisfies the equation AA^(-1) = I, where I is the identity matrix.To find the inverse of a matrix in Excel, we can use the MINVERSE function. This function takes a matrix as input and returns its inverse. We can then multiply the inverse by the constant matrix B to get the solution.
Using Gaussian Elimination
Gaussian elimination is another method for solving matrix equations. It involves transforming the coefficient matrix A into upper triangular form and then solving for the unknowns. This method is more efficient than the inverse matrix method for large matrices.To perform Gaussian elimination in Excel, we can use the MDETERM function to calculate the determinant of the coefficient matrix A. If the determinant is non-zero, we can then use the MINVERSE function to find the inverse of the matrix and solve for the unknowns.
Applications of Matrix Equations

Matrix equations have numerous applications in various fields, including:
- Physics: Matrix equations are used to describe the motion of objects, including the motion of particles and the vibration of systems.
- Engineering: Matrix equations are used to design and optimize systems, including electronic circuits and mechanical systems.
- Economics: Matrix equations are used to model the behavior of markets and to make predictions about economic trends.
- Computer science: Matrix equations are used in computer graphics, machine learning, and data analysis.
In each of these fields, matrix equations provide a powerful tool for solving complex problems and making predictions.
Physics Applications
In physics, matrix equations are used to describe the motion of objects. For example, the motion of a particle can be described by a matrix equation that relates the position and velocity of the particle to the forces acting on it.Engineering Applications
In engineering, matrix equations are used to design and optimize systems. For example, the design of an electronic circuit can be represented by a matrix equation that relates the input and output signals to the components of the circuit.Economics Applications
In economics, matrix equations are used to model the behavior of markets. For example, the behavior of a market can be represented by a matrix equation that relates the supply and demand of a product to the price of the product.Solving Matrix Equations in Excel
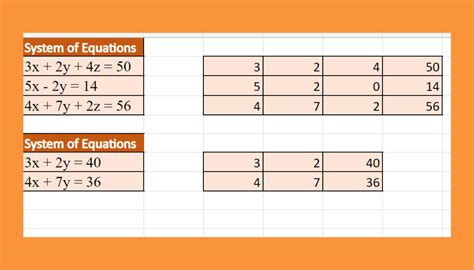
To solve a matrix equation in Excel, we can use the built-in functions, such as MINVERSE and MMULT. We can also use add-ins, such as the Analysis ToolPak, to solve matrix equations.
The steps to solve a matrix equation in Excel are:
- Enter the coefficient matrix A and the constant matrix B into separate ranges.
- Use the MINVERSE function to find the inverse of the coefficient matrix A.
- Multiply the inverse of the coefficient matrix A by the constant matrix B to get the solution.
We can also use the MMULT function to multiply the inverse of the coefficient matrix A by the constant matrix B.
Using the MINVERSE Function
The MINVERSE function is used to find the inverse of a matrix. The syntax of the MINVERSE function is MINVERSE(array), where array is the range of cells that contains the matrix.To use the MINVERSE function, we can select a range of cells and enter the formula =MINVERSE(A1:C3), where A1:C3 is the range of cells that contains the matrix.
Using the MMULT Function
The MMULT function is used to multiply two matrices. The syntax of the MMULT function is MMULT(array1, array2), where array1 and array2 are the ranges of cells that contain the matrices.To use the MMULT function, we can select a range of cells and enter the formula =MMULT(A1:C3, E1:G3), where A1:C3 and E1:G3 are the ranges of cells that contain the matrices.
Matrix Equations Image Gallery










What is a matrix equation?
+A matrix equation is an equation that involves a matrix, which is a rectangular array of numbers.
How do I solve a matrix equation in Excel?
+To solve a matrix equation in Excel, you can use the built-in functions, such as MINVERSE and MMULT, or add-ins, such as the Analysis ToolPak.
What are the applications of matrix equations?
+Matrix equations have numerous applications in various fields, including physics, engineering, economics, and computer science.
In conclusion, matrix equations are a powerful tool for solving complex problems and making predictions. They have numerous applications in various fields, including physics, engineering, economics, and computer science. In Excel, matrix equations can be solved using the built-in functions, such as MINVERSE and MMULT, or add-ins, such as the Analysis ToolPak. We hope this article has provided you with a comprehensive understanding of matrix equations and how to solve them in Excel. If you have any further questions or would like to learn more about matrix equations, please do not hesitate to comment or share this article with others.