Intro
Learn 5 ways to convert fractions to decimals, percentages, and mixed numbers with ease, mastering fraction conversion, decimal equivalents, and percentage calculations.
Converting fractions is an essential skill in mathematics, and it can be achieved in various ways. Fractions are used to represent a part of a whole, and understanding how to convert them is crucial for problem-solving in different areas of mathematics, such as algebra, geometry, and calculus. In this article, we will explore five ways to convert fractions, including converting improper fractions to mixed numbers, converting mixed numbers to improper fractions, converting fractions to decimals, converting decimals to fractions, and converting fractions to percentages.
The importance of converting fractions cannot be overstated. It is a fundamental concept in mathematics that has numerous applications in real-life situations. For instance, fractions are used in cooking, where recipes often require measuring ingredients in fractional amounts. Fractions are also used in science, where measurements are often taken in fractional units. Moreover, fractions are used in finance, where investments and interest rates are often expressed as fractions. Therefore, understanding how to convert fractions is essential for anyone who wants to develop a strong foundation in mathematics.
Converting fractions can seem daunting, especially for those who are new to mathematics. However, with practice and patience, anyone can master the art of converting fractions. There are various methods and techniques that can be used to convert fractions, and each method has its own advantages and disadvantages. In this article, we will explore five ways to convert fractions, and we will provide examples and illustrations to help readers understand each method.
Introduction to Fraction Conversion
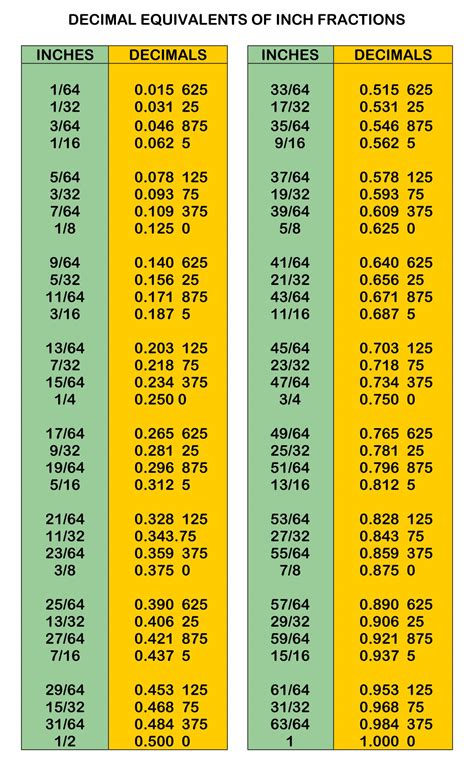
Fraction conversion is the process of changing a fraction from one form to another. There are several types of fraction conversions, including converting improper fractions to mixed numbers, converting mixed numbers to improper fractions, converting fractions to decimals, converting decimals to fractions, and converting fractions to percentages. Each type of conversion has its own set of rules and procedures, and understanding these rules is essential for accurate conversion.
Types of Fraction Conversions
There are several types of fraction conversions, and each type has its own unique characteristics. The most common types of fraction conversions are: * Converting improper fractions to mixed numbers * Converting mixed numbers to improper fractions * Converting fractions to decimals * Converting decimals to fractions * Converting fractions to percentagesConverting Improper Fractions to Mixed Numbers

Converting improper fractions to mixed numbers is a common type of fraction conversion. An improper fraction is a fraction where the numerator is greater than the denominator. To convert an improper fraction to a mixed number, we need to divide the numerator by the denominator and write the remainder as a fraction. For example, to convert the improper fraction 7/4 to a mixed number, we divide 7 by 4 and get 1 with a remainder of 3. Therefore, the mixed number equivalent of 7/4 is 1 3/4.
The steps to convert an improper fraction to a mixed number are:
- Divide the numerator by the denominator
- Write the quotient as the whole number part of the mixed number
- Write the remainder as the fraction part of the mixed number
Examples of Converting Improper Fractions to Mixed Numbers
Here are some examples of converting improper fractions to mixed numbers: * 9/4 = 2 1/4 * 11/6 = 1 5/6 * 15/8 = 1 7/8Converting Mixed Numbers to Improper Fractions

Converting mixed numbers to improper fractions is another common type of fraction conversion. A mixed number is a number that consists of a whole number part and a fraction part. To convert a mixed number to an improper fraction, we need to multiply the whole number part by the denominator and add the numerator. For example, to convert the mixed number 2 3/4 to an improper fraction, we multiply 2 by 4 and add 3, and then write the result over the denominator. Therefore, the improper fraction equivalent of 2 3/4 is 11/4.
The steps to convert a mixed number to an improper fraction are:
- Multiply the whole number part by the denominator
- Add the numerator to the product
- Write the result over the denominator
Examples of Converting Mixed Numbers to Improper Fractions
Here are some examples of converting mixed numbers to improper fractions: * 1 1/2 = 3/2 * 2 3/4 = 11/4 * 3 1/2 = 7/2Converting Fractions to Decimals

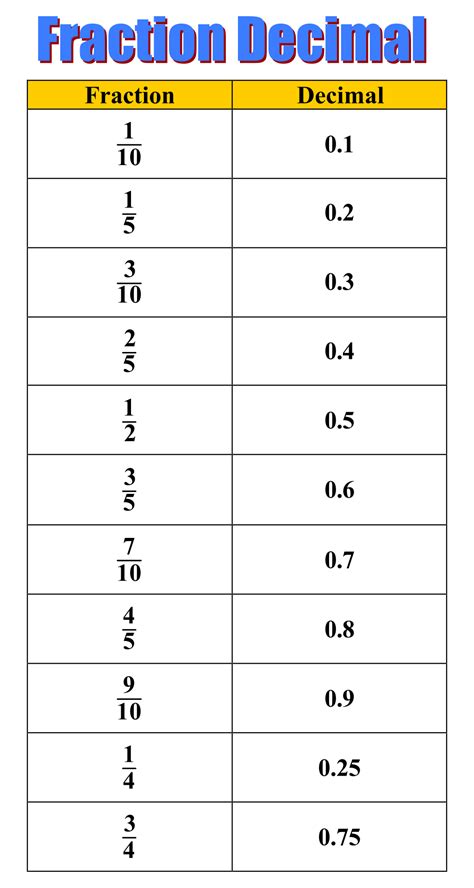
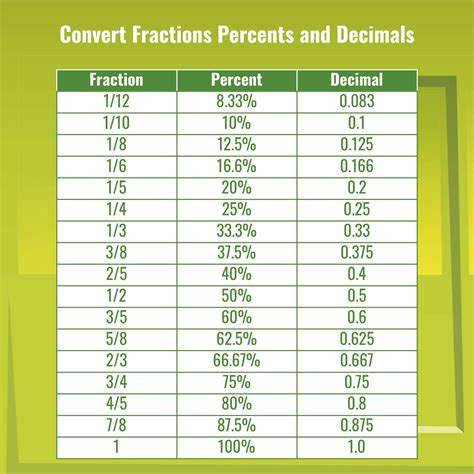
Converting fractions to decimals is a common type of fraction conversion. To convert a fraction to a decimal, we need to divide the numerator by the denominator. For example, to convert the fraction 3/4 to a decimal, we divide 3 by 4 and get 0.75. Therefore, the decimal equivalent of 3/4 is 0.75.
The steps to convert a fraction to a decimal are:
- Divide the numerator by the denominator
- Write the result as a decimal
Examples of Converting Fractions to Decimals
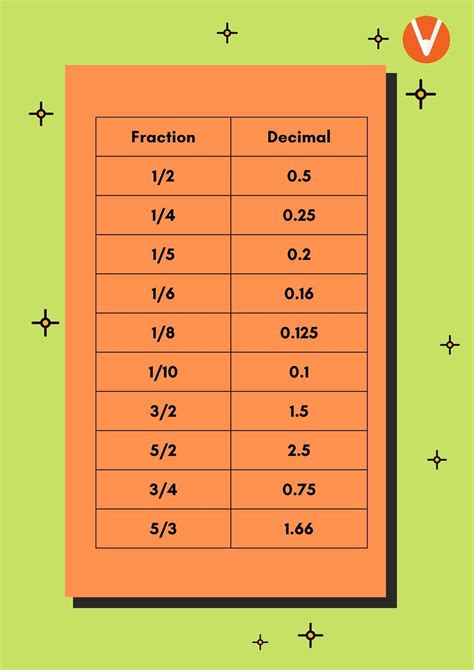
Here are some examples of converting fractions to decimals: * 1/2 = 0.5 * 3/4 = 0.75 * 2/3 = 0.67Converting Decimals to Fractions
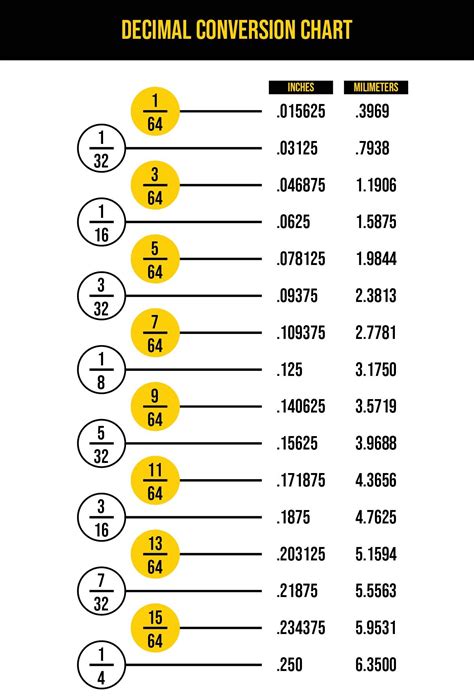
Converting decimals to fractions is another common type of fraction conversion. To convert a decimal to a fraction, we need to write the decimal as a fraction with a denominator of 10, 100, or 1000, depending on the number of decimal places. For example, to convert the decimal 0.75 to a fraction, we write it as 75/100 and simplify it to 3/4. Therefore, the fraction equivalent of 0.75 is 3/4.
The steps to convert a decimal to a fraction are:
- Write the decimal as a fraction with a denominator of 10, 100, or 1000
- Simplify the fraction
Examples of Converting Decimals to Fractions
Here are some examples of converting decimals to fractions: * 0.5 = 1/2 * 0.75 = 3/4 * 0.25 = 1/4Converting Fractions to Percentages
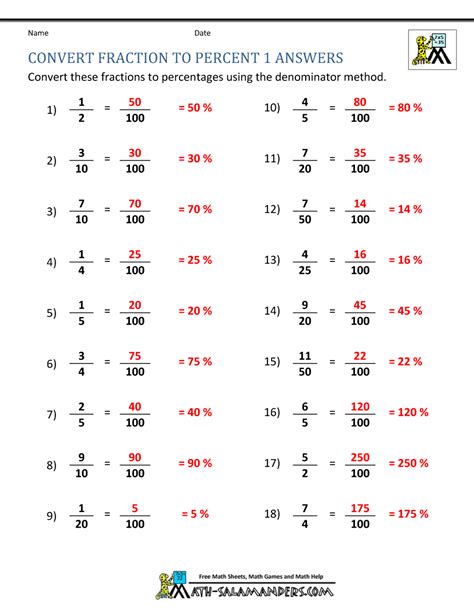
Converting fractions to percentages is a common type of fraction conversion. To convert a fraction to a percentage, we need to divide the numerator by the denominator and multiply the result by 100. For example, to convert the fraction 3/4 to a percentage, we divide 3 by 4 and multiply the result by 100, and get 75%. Therefore, the percentage equivalent of 3/4 is 75%.
The steps to convert a fraction to a percentage are:
- Divide the numerator by the denominator
- Multiply the result by 100
Examples of Converting Fractions to Percentages
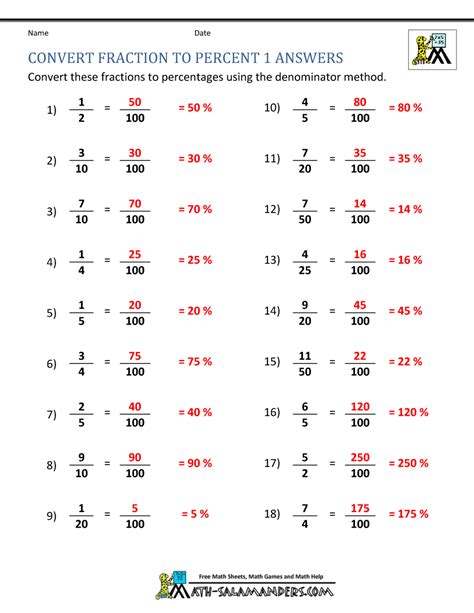
Here are some examples of converting fractions to percentages: * 1/2 = 50% * 3/4 = 75% * 2/3 = 67%Fraction Conversion Image Gallery
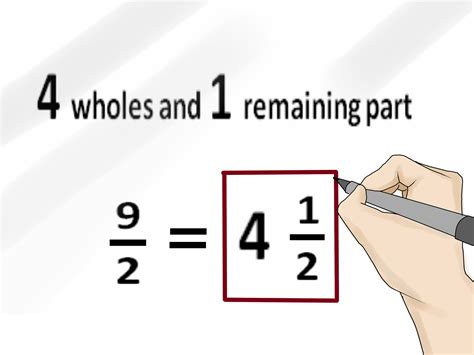
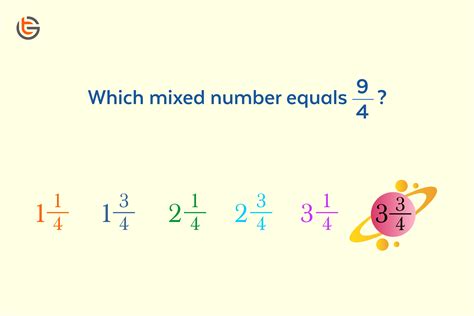



What is fraction conversion?
+Fraction conversion is the process of changing a fraction from one form to another.
What are the different types of fraction conversions?
+The different types of fraction conversions include converting improper fractions to mixed numbers, converting mixed numbers to improper fractions, converting fractions to decimals, converting decimals to fractions, and converting fractions to percentages.
How do I convert an improper fraction to a mixed number?
+To convert an improper fraction to a mixed number, divide the numerator by the denominator and write the remainder as a fraction.
How do I convert a decimal to a fraction?
+To convert a decimal to a fraction, write the decimal as a fraction with a denominator of 10, 100, or 1000, depending on the number of decimal places, and simplify the fraction.
What is the importance of fraction conversion in real-life situations?
+Fraction conversion is essential in real-life situations, such as cooking, science, and finance, where measurements are often taken in fractional units.
In conclusion, converting fractions is an essential skill in mathematics that has numerous applications in real-life situations. There are various methods and techniques that can be used to convert fractions, and each method has its own advantages and disadvantages. By understanding the different types of fraction conversions and how to apply them, individuals can develop a strong foundation in mathematics and improve their problem-solving skills. We hope that this article has provided readers with a comprehensive understanding of fraction conversion and its importance in mathematics. If you have any questions or comments, please feel free to share them with us. Additionally, if you found this article helpful, please share it with others who may benefit from it.