Intro
Discover 5 ways to check normality, ensuring data distribution is Gaussian. Learn normality tests, statistical methods, and data analysis techniques for accurate results.
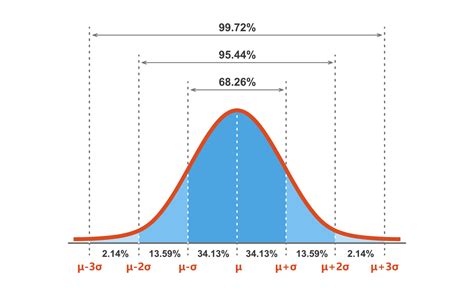
Normality is a fundamental concept in statistics that refers to the distribution of data following a bell-shaped curve, also known as the Gaussian distribution. Checking for normality is crucial in statistical analysis, as many statistical tests and models assume that the data follows a normal distribution. In this article, we will explore five ways to check for normality in a dataset.
The importance of checking for normality cannot be overstated. Many statistical tests, such as the t-test and analysis of variance (ANOVA), assume that the data follows a normal distribution. If the data is not normally distributed, these tests may not be valid, and the results may be misleading. Therefore, it is essential to check for normality before conducting any statistical analysis.
Normality checking is a critical step in data analysis, and it can help researchers and data analysts to identify potential issues with their data. By checking for normality, researchers can determine whether their data is suitable for parametric tests or if they need to use non-parametric tests. Additionally, normality checking can help researchers to identify outliers and anomalies in their data, which can be useful in data cleaning and preprocessing.
In the following sections, we will discuss five ways to check for normality in a dataset. These methods include visual inspection, the Shapiro-Wilk test, the Kolmogorov-Smirnov test, the Anderson-Darling test, and the Q-Q plot.
Visual Inspection

Advantages and Disadvantages of Visual Inspection
Visual inspection has several advantages, including its simplicity and ease of use. However, it also has some disadvantages, such as its subjectivity and lack of precision. Visual inspection can be influenced by the researcher's personal biases and expectations, and it may not be effective for large datasets.Shapiro-Wilk Test
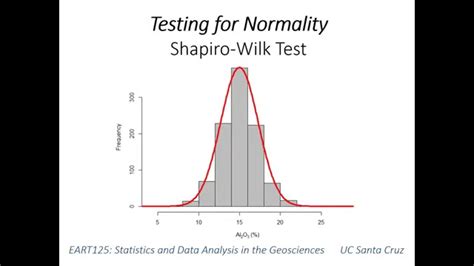
Interpreting the Shapiro-Wilk Test Results
The Shapiro-Wilk test results can be interpreted by comparing the W-statistic to a critical value. If the W-statistic is greater than the critical value, the null hypothesis of normality is not rejected, and the data is likely to be normally distributed. However, if the W-statistic is less than the critical value, the null hypothesis is rejected, and the data is likely to be non-normally distributed.Kolmogorov-Smirnov Test

Advantages and Disadvantages of the Kolmogorov-Smirnov Test
The Kolmogorov-Smirnov test has several advantages, including its ability to detect deviations from normality in the tails of the distribution. However, it also has some disadvantages, such as its sensitivity to sample size and its lack of power for small samples.Anderson-Darling Test
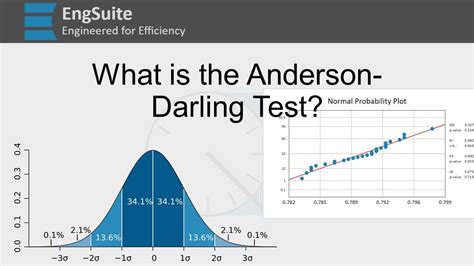
Interpreting the Anderson-Darling Test Results
The Anderson-Darling test results can be interpreted by comparing the A-statistic to a critical value. If the A-statistic is less than the critical value, the null hypothesis of normality is not rejected, and the data is likely to be normally distributed. However, if the A-statistic is greater than the critical value, the null hypothesis is rejected, and the data is likely to be non-normally distributed.Q-Q Plot
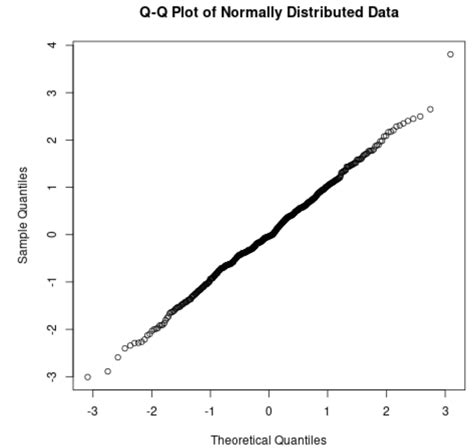
Advantages and Disadvantages of the Q-Q Plot
The Q-Q plot has several advantages, including its ability to detect deviations from normality in the tails of the distribution. However, it also has some disadvantages, such as its subjectivity and lack of precision.Normality Checking Image Gallery






What is normality in statistics?
+Normality in statistics refers to the distribution of data following a bell-shaped curve, also known as the Gaussian distribution.
Why is normality checking important in statistics?
+Normality checking is important in statistics because many statistical tests and models assume that the data follows a normal distribution. If the data is not normally distributed, these tests may not be valid, and the results may be misleading.
What are the methods for checking normality in statistics?
+The methods for checking normality in statistics include visual inspection, the Shapiro-Wilk test, the Kolmogorov-Smirnov test, the Anderson-Darling test, and the Q-Q plot.
How do I interpret the results of a normality test?
+The results of a normality test can be interpreted by comparing the test statistic to a critical value. If the test statistic is less than the critical value, the null hypothesis of normality is not rejected, and the data is likely to be normally distributed. However, if the test statistic is greater than the critical value, the null hypothesis is rejected, and the data is likely to be non-normally distributed.
What are the advantages and disadvantages of each normality test?
+Each normality test has its advantages and disadvantages. For example, the Shapiro-Wilk test is sensitive to sample size, while the Kolmogorov-Smirnov test is sensitive to the tails of the distribution. The Q-Q plot is a graphical method that can be used to detect deviations from normality, but it is subjective and lacks precision.
In conclusion, checking for normality is an essential step in statistical analysis. By using one or more of the methods discussed in this article, researchers and data analysts can determine whether their data is normally distributed and choose the appropriate statistical tests and models. We hope this article has provided you with a comprehensive understanding of normality checking and its importance in statistics. If you have any questions or comments, please do not hesitate to share them with us.