Determinant Of 3x3 Matrix Worksheet

The determinant of a 3x3 matrix is a fundamental concept in linear algebra, and it has numerous applications in various fields, including mathematics, physics, engineering, and computer science. In this article, we will delve into the world of 3x3 matrices and explore the concept of determinants, providing a comprehensive guide on how to calculate them.

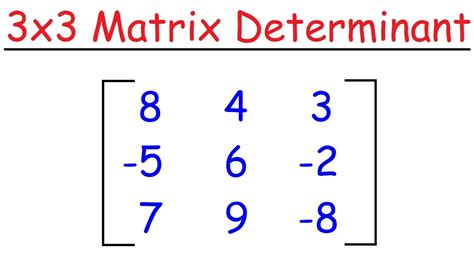
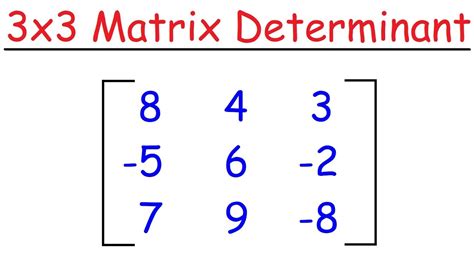
To begin with, a 3x3 matrix is a square matrix with three rows and three columns. It can be represented as:

| a  b  c |
| d  e  f |
| g  h  i |

where a, b, c, d, e, f, g, h, and i are the elements of the matrix. The determinant of this matrix is denoted as det(A) or |A|, and it can be calculated using various methods.

Introduction to Determinants

The determinant of a 3x3 matrix is a scalar value that can be used to describe the properties of the matrix. It is a measure of the "volume" of the parallelepiped formed by the column vectors of the matrix. In other words, it represents the amount of stretching or shrinking that occurs when the matrix is applied to a vector.

Methods for Calculating Determinants

There are several methods for calculating the determinant of a 3x3 matrix, including:

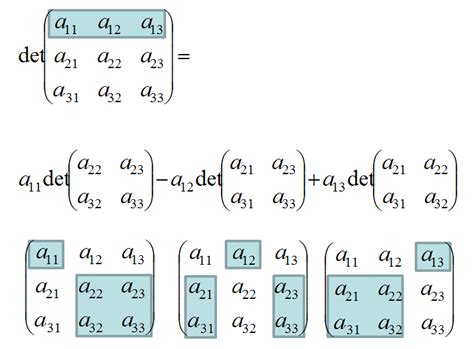
Expansion by minors: This method involves breaking down the matrix into smaller 2x2 submatrices and calculating their determinants.
Rule of Sarrus: This method involves using a specific pattern to calculate the determinant of the matrix.
Laplace expansion: This method involves expanding the determinant along a row or column of the matrix.

Expansion by Minors

The expansion by minors method involves breaking down the matrix into smaller 2x2 submatrices and calculating their determinants. The formula for this method is: ``` det(A) = a(ei - fh) - b(di - fg) + c(dh - eg) ``` where a, b, c, d, e, f, g, h, and i are the elements of the matrix.

Rule of Sarrus

The rule of Sarrus is a simple method for calculating the determinant of a 3x3 matrix. The formula for this method is: ``` det(A) = a(ei - fh) + b(fg - di) + c(dh - eg) ``` This method involves using a specific pattern to calculate the determinant of the matrix.

Laplace Expansion

The Laplace expansion method involves expanding the determinant along a row or column of the matrix. The formula for this method is: ``` det(A) = a(ei - fh) - b(di - fg) + c(dh - eg) ``` This method is similar to the expansion by minors method, but it involves expanding the determinant along a row or column of the matrix.

Benefits of Calculating Determinants

Calculating the determinant of a 3x3 matrix has several benefits, including:

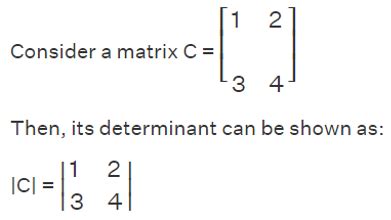
Solving systems of linear equations: The determinant can be used to solve systems of linear equations by finding the inverse of the matrix.
Finding the inverse of a matrix: The determinant can be used to find the inverse of a matrix, which is essential in many applications.
Determining the solvability of a system: The determinant can be used to determine whether a system of linear equations has a unique solution, no solution, or infinitely many solutions.

Applications of Determinants

Determinants have numerous applications in various fields, including:

Mathematics: Determinants are used to solve systems of linear equations, find the inverse of a matrix, and determine the solvability of a system.
Physics: Determinants are used to describe the motion of objects, calculate the force and torque on an object, and determine the stability of a system.
Engineering: Determinants are used to design and analyze systems, calculate the stress and strain on a material, and determine the stability of a structure.
Computer Science: Determinants are used in computer graphics, game development, and machine learning.

Common Mistakes to Avoid

When calculating the determinant of a 3x3 matrix, there are several common mistakes to avoid, including:

Forgetting to expand the determinant along a row or column
Incorrectly calculating the minors
Forgetting to subtract the product of the diagonal elements

Tips for Calculating Determinants

Here are some tips for calculating the determinant of a 3x3 matrix:

Use the expansion by minors method or the rule of Sarrus to calculate the determinant.
Double-check your calculations to ensure accuracy.
Use a calculator or computer program to verify your results.

Conclusion and Final Thoughts

In conclusion, calculating the determinant of a 3x3 matrix is a fundamental concept in linear algebra, and it has numerous applications in various fields. By using the expansion by minors method, the rule of Sarrus, or the Laplace expansion method, you can calculate the determinant of a 3x3 matrix with ease. Remember to avoid common mistakes and use tips and tricks to ensure accuracy.

Determinant of 3x3 Matrix Image Gallery

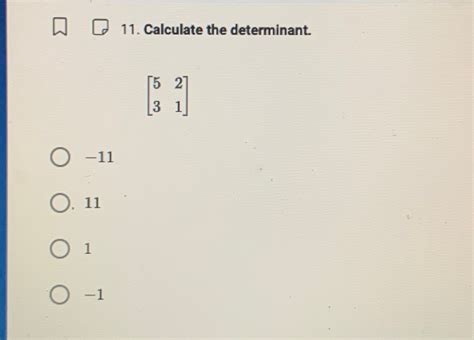
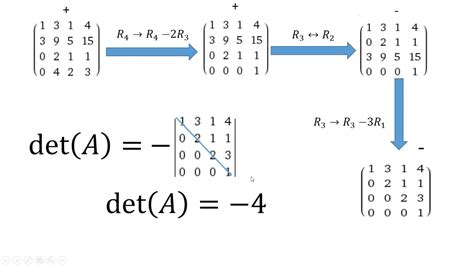
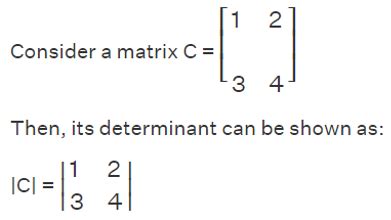
What is the determinant of a 3x3 matrix?

How do I calculate the determinant of a 3x3 matrix?

There are several methods for calculating the determinant of a 3x3 matrix, including expansion by minors, the rule of Sarrus, and Laplace expansion.

What are the benefits of calculating the determinant of a 3x3 matrix?

Calculating the determinant of a 3x3 matrix has several benefits, including solving systems of linear equations, finding the inverse of a matrix, and determining the solvability of a system.

We hope this article has provided you with a comprehensive guide on how to calculate the determinant of a 3x3 matrix. Whether you're a student, teacher, or professional, we encourage you to share your thoughts and experiences with us in the comments section below. Don't forget to share this article with your friends and colleagues who may benefit from it. Thank you for reading!