Empirical Rule Formula Excel

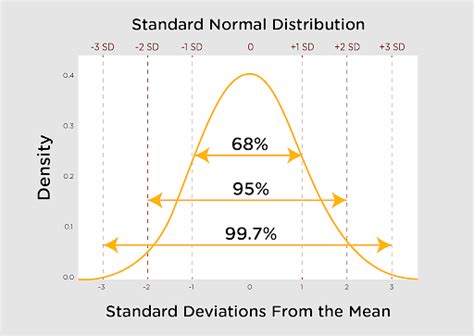
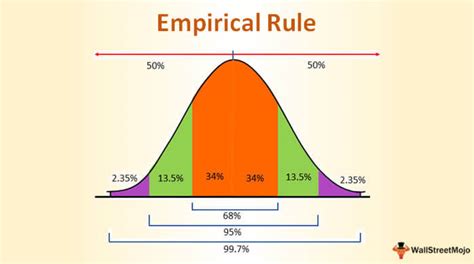
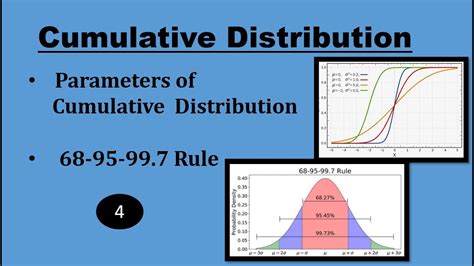
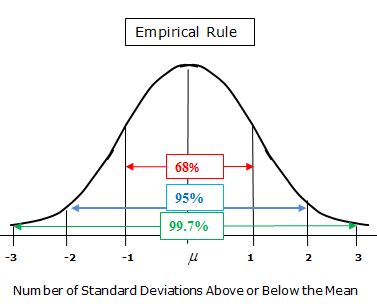
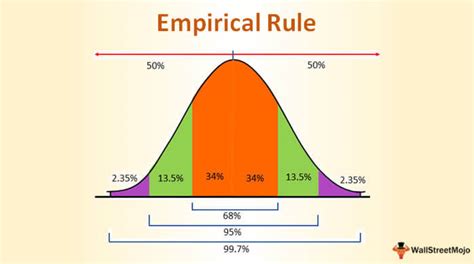
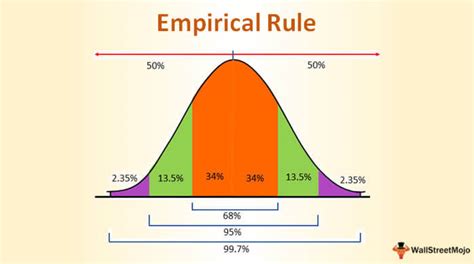
The empirical rule, also known as the 68-95-99.7 rule, is a statistical principle that describes the distribution of data in a normal distribution. It states that about 68% of the data falls within one standard deviation of the mean, about 95% falls within two standard deviations, and about 99.7% falls within three standard deviations. In this article, we will explore the empirical rule formula in Excel and its applications.

The empirical rule is a powerful tool for understanding and analyzing data. It provides a simple and effective way to understand the distribution of data and make predictions about future outcomes. The empirical rule is widely used in statistics, engineering, economics, and other fields where data analysis is crucial.

To apply the empirical rule in Excel, you need to calculate the mean and standard deviation of your data. The mean is the average value of the data, and the standard deviation is a measure of the spread or dispersion of the data. Once you have calculated the mean and standard deviation, you can use the empirical rule formula to determine the range of values that fall within one, two, or three standard deviations of the mean.

Empirical Rule Formula

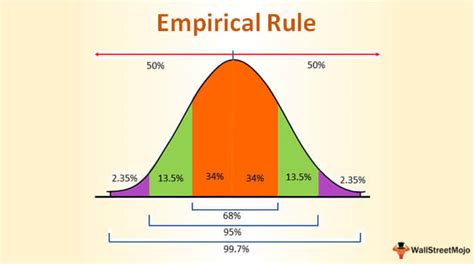
The empirical rule formula is based on the normal distribution curve, which is symmetric and bell-shaped. The formula states that:

About 68% of the data falls within one standard deviation of the mean (μ ± σ)
About 95% of the data falls within two standard deviations of the mean (μ ± 2σ)
About 99.7% of the data falls within three standard deviations of the mean (μ ± 3σ)

Where μ is the mean and σ is the standard deviation.

Calculating the Mean and Standard Deviation in Excel

To calculate the mean and standard deviation in Excel, you can use the following formulas:

Mean: =AVERAGE(range)
Standard Deviation: =STDEV(range)

Where range is the range of cells that contain your data.

For example, if your data is in the range A1:A10, you can calculate the mean and standard deviation as follows:

Mean: =AVERAGE(A1:A10)
Standard Deviation: =STDEV(A1:A10)

Applying the Empirical Rule in Excel

Once you have calculated the mean and standard deviation, you can apply the empirical rule to determine the range of values that fall within one, two, or three standard deviations of the mean.

For example, if the mean is 10 and the standard deviation is 2, you can calculate the range of values as follows:

One standard deviation: 10 ± 2 = 8 to 12
Two standard deviations: 10 ± 2(2) = 6 to 14
Three standard deviations: 10 ± 3(2) = 4 to 16

This means that about 68% of the data falls within the range of 8 to 12, about 95% falls within the range of 6 to 14, and about 99.7% falls within the range of 4 to 16.

Practical Applications of the Empirical Rule

The empirical rule has many practical applications in statistics, engineering, economics, and other fields. Some examples include:

Quality control: The empirical rule can be used to determine the range of values that are within acceptable limits.
Forecasting: The empirical rule can be used to make predictions about future outcomes based on historical data.
Risk analysis: The empirical rule can be used to determine the likelihood of extreme events.

Limitations of the Empirical Rule

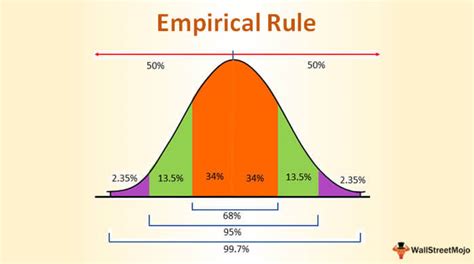
While the empirical rule is a powerful tool for understanding and analyzing data, it has some limitations. Some of these limitations include:

The empirical rule assumes a normal distribution, which may not always be the case.
The empirical rule does not provide a exact probability of extreme events, but rather a rough estimate.
The empirical rule is sensitive to outliers, which can affect the accuracy of the results.

Conclusion and Future Directions

In conclusion, the empirical rule is a powerful tool for understanding and analyzing data. It provides a simple and effective way to understand the distribution of data and make predictions about future outcomes. However, it is important to be aware of the limitations of the empirical rule and to use it in conjunction with other statistical tools and techniques.

As data analysis continues to play an increasingly important role in many fields, the empirical rule is likely to remain a widely used and useful tool. Future directions for research and development may include the development of new statistical tools and techniques that can be used in conjunction with the empirical rule, as well as the application of the empirical rule to new and emerging fields such as machine learning and artificial intelligence.

Gallery of Empirical Rule Applications

Empirical Rule Image Gallery

What is the empirical rule?

The empirical rule is a statistical principle that describes the distribution of data in a normal distribution. It states that about 68% of the data falls within one standard deviation of the mean, about 95% falls within two standard deviations, and about 99.7% falls within three standard deviations.

How is the empirical rule used in Excel?

The empirical rule is used in Excel to calculate the range of values that fall within one, two, or three standard deviations of the mean. This is done by calculating the mean and standard deviation of the data, and then applying the empirical rule formula.

What are the limitations of the empirical rule?

The empirical rule has several limitations, including the assumption of a normal distribution, sensitivity to outliers, and the provision of only a rough estimate of the probability of extreme events.

We hope this article has provided a comprehensive overview of the empirical rule formula in Excel and its applications. If you have any questions or comments, please don't hesitate to reach out. We encourage you to share this article with others who may be interested in learning more about the empirical rule and its uses. Additionally, we invite you to explore our other articles and resources on statistics and data analysis. Thank you for reading!