Intro
Understanding and working with functions is a crucial part of mathematics and other fields like computer science and engineering. A function is essentially a relation between a set of inputs, known as the domain, and a set of possible outputs, known as the range. For students and professionals alike, mastering functions can be challenging, but with the right approach and tools, it becomes more manageable. Here are some tips and explanations to help you work with function worksheets effectively.
Working with functions involves understanding their definitions, types, and applications. It requires a strong foundation in algebra and mathematical reasoning. Whether you're dealing with linear, quadratic, polynomial, or rational functions, each type has its unique characteristics and rules. For instance, linear functions are defined by the equation y = mx + b, where m is the slope and b is the y-intercept. Understanding these basics is key to solving problems on function worksheets.
As you delve into more complex functions, such as exponential and logarithmic functions, the concepts of growth and decay, and the properties of logarithms, become essential. The ability to graph these functions and understand their behavior is also critical. Graphing involves identifying key points like the x and y intercepts, vertex for quadratic functions, and asymptotes for rational functions. Each of these elements provides valuable information about the function's behavior and can be crucial in solving problems.
Understanding Function Notation

Function notation is a way of writing functions using letters and symbols. For example, f(x) represents the output of the function f when the input is x. Understanding function notation is vital because it allows you to communicate mathematical ideas clearly and concisely. When working with function worksheets, being able to interpret and apply function notation correctly can simplify the process of solving problems.
Graphing Functions
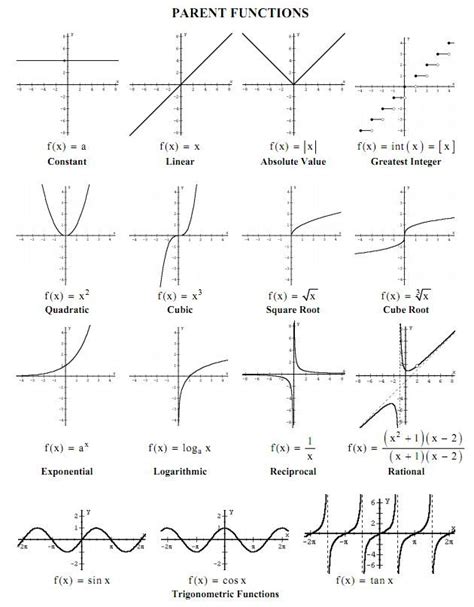
Graphing functions visually represents the relationship between the inputs and outputs of a function. It's a powerful tool for understanding function behavior, identifying patterns, and solving equations. There are several methods to graph functions, including plotting points, using a graphing calculator, or applying transformations to basic function graphs. Each method has its advantages, and choosing the right one depends on the specific function and the information you need to extract.
Steps to Graph a Function
To graph a function, follow these steps:
- Identify the function type: Determine if it's linear, quadratic, polynomial, etc.
- Find key points: Calculate the x and y intercepts, and for quadratic functions, find the vertex.
- Use a graphing method: Plot points, use a graphing calculator, or apply transformations.
- Check for asymptotes: Especially important for rational functions.
- Analyze the graph: Understand the function's behavior, including its domain and range.
Function Operations

Function operations involve adding, subtracting, multiplying, and dividing functions. These operations are defined in terms of the operations on their outputs. For example, to add two functions f and g, you add their outputs for each input: (f + g)(x) = f(x) + g(x). Understanding how to perform these operations is essential for simplifying expressions, solving equations, and modeling real-world phenomena.
Types of Function Operations
- Addition and Subtraction: Combine functions by adding or subtracting their outputs.
- Multiplication and Division: Similarly, combine functions by multiplying or dividing their outputs.
- Composition: Combine functions by using the output of one function as the input for another.
Applying Functions to Real-World Problems

Functions are not just abstract mathematical concepts; they have numerous practical applications. In physics, functions describe the motion of objects and the forces acting upon them. In economics, functions model supply and demand, and in computer science, functions are fundamental in programming. Being able to apply functions to real-world problems involves identifying the key variables and relationships and then selecting or constructing an appropriate function to model the situation.
Examples of Real-World Applications
- Physics and Engineering: Modeling motion, forces, and energy changes.
- Economics: Analyzing supply and demand, economic growth, and cost functions.
- Computer Science: Programming functions to perform specific tasks and operations.
Using Technology to Solve Function Problems

Technology, such as graphing calculators and computer software, can significantly aid in solving function problems. These tools can graph functions quickly and accurately, solve equations, and perform complex calculations. They are invaluable for exploring function behavior, testing hypotheses, and visualizing complex relationships.
Benefits of Using Technology
- Accuracy and Speed: Quickly and accurately graph functions and solve equations.
- Exploration: Easily explore how changes in a function affect its graph and behavior.
- Visualization: Visualize complex relationships and patterns that might be difficult to discern algebraically.
Conclusion and Next Steps

Mastering functions takes time and practice. By understanding function notation, graphing functions, performing function operations, applying functions to real-world problems, and utilizing technology, you can become proficient in working with functions. Remember, the key to success is consistent practice and applying what you learn to various scenarios.
Function Worksheet Image Gallery









What is the importance of understanding function notation?
+Understanding function notation is crucial because it allows for clear and concise communication of mathematical ideas and is fundamental in solving function problems.
How do I graph a function?
+To graph a function, identify the function type, find key points such as intercepts and the vertex for quadratic functions, and then use a graphing method such as plotting points or using a graphing calculator.
What are some real-world applications of functions?
+Functions have numerous real-world applications, including modeling motion and forces in physics, analyzing supply and demand in economics, and programming in computer science.
We hope this comprehensive guide to working with functions has been informative and helpful. Whether you're a student looking to improve your understanding of functions or a professional seeking to apply functions in your work, the tips and explanations provided here should serve as a valuable resource. Remember, practice is key, and applying what you learn to real-world scenarios will deepen your understanding and proficiency with functions. If you have any further questions or would like to explore more topics related to functions, don't hesitate to reach out or share your thoughts in the comments below.