Intro
Learn 5 ways to calculate deviation, including standard, mean, and average deviation methods, to measure data variability and dispersion in statistics, using formulas and examples for accurate calculation and analysis of data sets.
Understanding deviation is crucial in various fields, including statistics, finance, and engineering. It helps in measuring the spread or dispersion of data from its mean value. Calculating deviation is essential for assessing risk, making predictions, and understanding the variability within a dataset. There are several methods to calculate deviation, each serving a different purpose or offering a unique perspective on the data. Here, we'll explore five ways to calculate deviation, diving into their formulas, applications, and interpretations.
The importance of calculating deviation cannot be overstated. It provides insights into how data points are spread out, which is vital for decision-making in many areas. For instance, in finance, understanding the standard deviation of stock prices helps investors gauge the volatility and potential risk of their investments. In engineering, calculating deviation is critical for ensuring that manufactured parts meet specific tolerance standards, thereby affecting the performance and safety of the final product.
Moreover, deviation calculations are fundamental in statistical analysis. They help researchers understand the distribution of their data, identify outliers, and apply appropriate statistical models. The choice of method for calculating deviation depends on the nature of the data, the purpose of the analysis, and the level of detail required. Whether it's for academic research, business analytics, or quality control, mastering these methods is indispensable for anyone working with data.
Introduction to Deviation Calculations

Deviation calculations are integral to understanding data variability. The most common types include mean deviation, standard deviation, variance, average absolute deviation, and median absolute deviation. Each of these measures offers a unique insight into how data points deviate from a central tendency measure, such as the mean or median.
Mean Deviation

Mean deviation, also known as mean absolute deviation (MAD), measures the average distance of data points from the mean. It's calculated by summing the absolute differences between each data point and the mean, then dividing by the number of data points. The formula for mean deviation is: [ \text{Mean Deviation} = \frac{\sum_{i=1}^{n} |x_i - \bar{x}|}{n} ] where (x_i) represents each data point, (\bar{x}) is the mean of the dataset, and (n) is the total number of data points.
Applications of Mean Deviation
Mean deviation is useful for understanding the spread of data when the mean is an appropriate central tendency measure. It's particularly valuable in financial analyses, such as assessing the risk of investment portfolios, where the average deviation from expected returns is crucial.
Standard Deviation

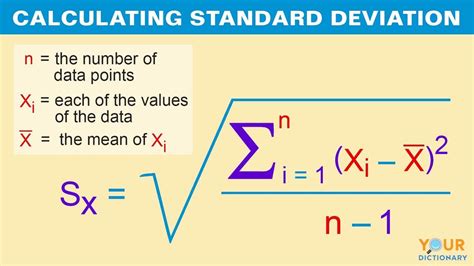
Standard deviation is a widely used measure of dispersion that quantifies the amount of variation or dispersion of a set of data values. It's calculated as the square root of the variance, which is the average of the squared differences from the mean. The formula for standard deviation is: [ \sigma = \sqrt{\frac{\sum_{i=1}^{n} (x_i - \bar{x})^2}{n-1}} ] for sample standard deviation, where (n-1) is used for Bessel's correction to get a more accurate estimate of the population standard deviation.
Interpretation of Standard Deviation
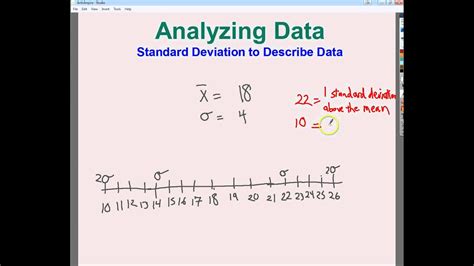
A small standard deviation indicates that the data points tend to be close to the mean, while a large standard deviation means that the data points are spread out over a wider range of values. Standard deviation is critical in statistical inference and is used extensively in hypothesis testing and confidence intervals.
Variance
Variance measures the average of the squared differences from the mean. It's essentially the square of the standard deviation. The formula for variance is: [ \sigma^2 = \frac{\sum_{i=1}^{n} (x_i - \bar{x})^2}{n-1} ] Variance gives an idea of how spread out the data is, but since it's in squared units, it's not as intuitive as standard deviation for interpretation.
Applications of Variance
Variance is fundamental in many statistical analyses, including regression analysis, where it's used to measure the goodness of fit of a model. It's also crucial in the calculation of standard deviation, which is more interpretable.
Average Absolute Deviation

Average absolute deviation is similar to mean deviation but is sometimes calculated without taking the absolute value, depending on the context. It's a measure of the average distance of data points from a central point, usually the mean.
Median Absolute Deviation
Median absolute deviation (MAD) measures the median of the absolute differences between each data point and the median of the dataset. It's more robust than mean deviation, especially in the presence of outliers, as it uses the median, which is less affected by extreme values.
Conclusion and Further Steps

Understanding and calculating deviation is a foundational aspect of data analysis. By mastering these methods, individuals can better comprehend their data, make more informed decisions, and apply statistical techniques effectively. Whether it's for professional analysis, academic research, or personal projects, the ability to calculate and interpret deviation is indispensable.
To further enhance your understanding, it's essential to practice applying these methods to real-world datasets. Experiment with different types of data and scenarios to see how deviation calculations can provide insights into variability and risk. Additionally, exploring advanced statistical concepts and tools can offer even more sophisticated ways to analyze and interpret data.
Gallery of Deviation Calculations
Deviation Calculations Image Gallery




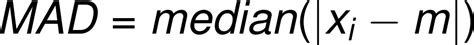



Frequently Asked Questions
What is the purpose of calculating deviation in statistics?
+Calculating deviation helps in understanding the spread or dispersion of data from its mean value, which is crucial for assessing risk, making predictions, and understanding variability within a dataset.
What are the different types of deviation calculations?
+The main types include mean deviation, standard deviation, variance, average absolute deviation, and median absolute deviation. Each offers a unique perspective on data variability.
How do I choose the right deviation calculation for my data?
+The choice depends on the nature of your data, the purpose of your analysis, and the level of detail you need. For example, standard deviation is commonly used for its interpretability, while median absolute deviation is more robust against outliers.
If you've found this article informative and helpful, we invite you to share your thoughts and experiences with deviation calculations in the comments below. Whether you're a seasoned statistician or just starting to explore the world of data analysis, your insights can enrich the discussion and help others deepen their understanding of this critical topic. Additionally, consider sharing this article with colleagues or peers who might benefit from learning about the different methods of calculating deviation and their applications. By spreading knowledge and fostering a community of learners, we can all become more adept at navigating and interpreting the complex world of data.