How To Calculate Ucl And Lcl In Excel

Calculating UCL (Upper Control Limit) and LCL (Lower Control Limit) in Excel is a crucial step in statistical process control. These limits help determine whether a process is in control or not. In this article, we will delve into the importance of UCL and LCL, their calculation, and how to apply them in Excel.

The UCL and LCL are essential components of control charts, which are graphical representations of a process over time. Control charts help identify trends, patterns, and anomalies in the data, enabling quality control professionals to take corrective actions when necessary. The UCL and LCL are calculated based on the mean and standard deviation of the process data.

To calculate UCL and LCL, you need to have a set of data that represents the process you want to control. This data can be in the form of measurements, such as weight, length, or temperature, or it can be in the form of counts, such as the number of defects per unit. The data should be collected over a period, and it's essential to have at least 20-30 data points to get a reliable estimate of the mean and standard deviation.

Understanding UCL and LCL

The UCL is the upper boundary of the control chart, and the LCL is the lower boundary. The UCL is calculated by adding 3 standard deviations to the mean, while the LCL is calculated by subtracting 3 standard deviations from the mean. This means that if the process is in control, 99.7% of the data points should fall within the UCL and LCL.

Calculating UCL and LCL in Excel

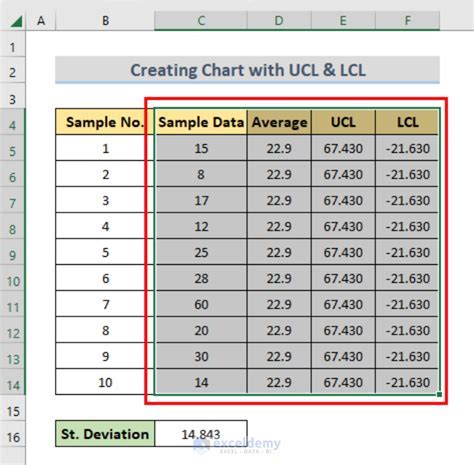
To calculate UCL and LCL in Excel, follow these steps:

Enter your data in a column, for example, column A.
Calculate the mean of the data using the formula: =AVERAGE(A1:A30).
Calculate the standard deviation of the data using the formula: =STDEV(A1:A30).
Calculate the UCL using the formula: =mean + 3*standard deviation.
Calculate the LCL using the formula: =mean - 3*standard deviation.

You can also use the following formulas to calculate UCL and LCL:

UCL: =AVERAGE(A1:A30) + 3*STDEV(A1:A30)
LCL: =AVERAGE(A1:A30) - 3*STDEV(A1:A30)

Interpreting UCL and LCL

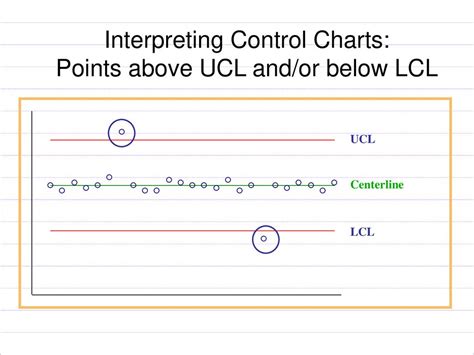
Once you have calculated the UCL and LCL, you can interpret the results as follows:

If all data points fall within the UCL and LCL, the process is in control.
If one or more data points fall outside the UCL or LCL, the process is out of control.
If the data points are consistently near the UCL or LCL, it may indicate that the process is drifting or trending.

Using UCL and LCL in Quality Control

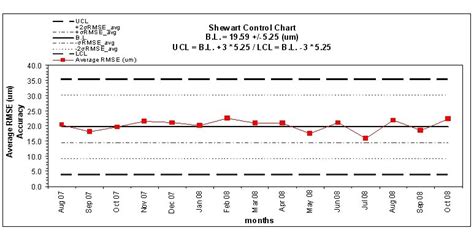
UCL and LCL are widely used in quality control to monitor and improve processes. By calculating and interpreting UCL and LCL, quality control professionals can:

Identify trends and patterns in the data
Detect anomalies and outliers
Take corrective actions to bring the process back in control
Improve process capability and reduce variability

Common Applications of UCL and LCL

UCL and LCL have numerous applications in various industries, including:

Manufacturing: to monitor and control production processes
Healthcare: to monitor patient outcomes and improve quality of care
Finance: to detect anomalies in financial transactions
Environmental monitoring: to detect changes in air and water quality

Best Practices for Calculating UCL and LCL

To ensure accurate and reliable calculations of UCL and LCL, follow these best practices:

Use a sufficient amount of data (at least 20-30 data points)
Ensure that the data is normally distributed
Use the correct formulas and calculations
Regularly update and recalculate UCL and LCL as new data becomes available

Gallery of UCL and LCL Examples

UCL and LCL Image Gallery

What is the purpose of calculating UCL and LCL?

The purpose of calculating UCL and LCL is to determine whether a process is in control or not. These limits help identify trends, patterns, and anomalies in the data, enabling quality control professionals to take corrective actions when necessary.

How do I calculate UCL and LCL in Excel?

To calculate UCL and LCL in Excel, enter your data in a column, calculate the mean and standard deviation, and then use the formulas: UCL = mean + 3*standard deviation and LCL = mean - 3*standard deviation.

What are the common applications of UCL and LCL?

UCL and LCL have numerous applications in various industries, including manufacturing, healthcare, finance, and environmental monitoring. They are used to monitor and control production processes, detect anomalies, and improve process capability and reduce variability.

In conclusion, calculating UCL and LCL is a crucial step in statistical process control. By understanding the importance of UCL and LCL, calculating them in Excel, and interpreting the results, quality control professionals can identify trends, patterns, and anomalies in the data and take corrective actions to improve process capability and reduce variability. We hope this article has provided you with a comprehensive understanding of UCL and LCL and their applications in quality control. If you have any further questions or would like to share your experiences with UCL and LCL, please feel free to comment below.