5 Ways Find Missing Number

The problem of finding a missing number in a sequence or series is a common challenge that can arise in various mathematical and real-world contexts. Whether you're dealing with a sequence of numbers, a pattern, or a mathematical series, identifying the missing element can be crucial for understanding and solving problems. There are several approaches and strategies that can be employed to find missing numbers, each suited to different types of sequences or patterns. Here, we'll explore five key methods that are widely applicable and useful.

Finding missing numbers is essential in mathematics and other fields like data analysis, coding, and puzzle-solving. It helps in identifying patterns, completing datasets, and solving complex problems. The methods to find missing numbers can range from simple arithmetic to more complex mathematical operations, depending on the nature of the sequence or series.

To begin with, let's consider a basic example where we have a simple arithmetic sequence: 2, 5, 8, _, 14. In this case, the difference between each consecutive pair of numbers is constant (3), which makes it easy to identify the missing number. However, sequences can be more complex, involving geometric patterns, algebraic expressions, or even statistical distributions.

Understanding Sequences and Patterns

Sequences and patterns are foundational concepts in mathematics. A sequence is a set of numbers that are in a particular order, and a pattern is the rule or method that describes how each term of the sequence is generated from the preceding term(s). Understanding the type of sequence or pattern (arithmetic, geometric, harmonic, etc.) is crucial for determining the missing number.

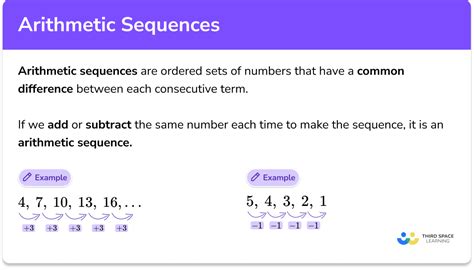
Method 1: Arithmetic Sequences

An arithmetic sequence is one in which the difference between consecutive terms is constant. For example, in the sequence 3, 6, 9, 12, the common difference is 3. To find a missing number in an arithmetic sequence, you need to identify the common difference and then apply it to find the missing term.

Steps for Arithmetic Sequences

1. Identify the first term and the common difference of the sequence.
2. Use the formula for the nth term of an arithmetic sequence: (a_n = a_1 + (n-1)d), where (a_n) is the nth term, (a_1) is the first term, (n) is the term number, and (d) is the common difference.
3. If the term number of the missing term is known, substitute the values into the formula to find the missing term.

Method 2: Geometric Sequences

A geometric sequence is one in which each term after the first is found by multiplying the previous one by a fixed, non-zero number called the common ratio. For example, in the sequence 2, 6, 18, 54, the common ratio is 3. Finding a missing number in a geometric sequence involves identifying the common ratio and applying it.

Steps for Geometric Sequences

1. Identify the first term and the common ratio of the sequence.
2. Use the formula for the nth term of a geometric sequence: (a_n = a_1 \cdot r^{(n-1)}), where (a_n) is the nth term, (a_1) is the first term, (r) is the common ratio, and (n) is the term number.
3. Substitute the known values into the formula to find the missing term.

Method 3: Algebraic Methods

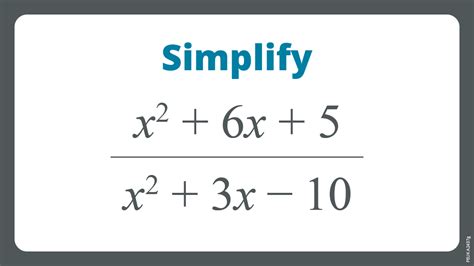
Algebraic methods involve using variables and equations to represent and solve problems involving sequences and patterns. This can include setting up equations based on the given terms of a sequence and solving for the missing term.

Steps for Algebraic Methods

1. Represent the sequence or pattern algebraically.
2. Set up an equation based on the information given about the sequence.
3. Solve the equation for the missing term.

Method 4: Pattern Recognition

Pattern recognition involves identifying the rule or pattern that generates the sequence. This can be more subjective and requires a good understanding of different types of sequences and patterns.

Steps for Pattern Recognition

1. Examine the sequence for common patterns such as arithmetic or geometric sequences.
2. Look for other patterns such as alternating addition and subtraction, or patterns involving operations with increasing or decreasing values.
3. Once the pattern is identified, apply it to find the missing term.

Method 5: Statistical Analysis

Statistical analysis can be used when dealing with large datasets or sequences that exhibit statistical patterns rather than deterministic ones. This involves using statistical methods to identify trends and predict missing values.

Steps for Statistical Analysis

1. Collect and analyze the data to identify any statistical trends or patterns.
2. Use statistical models such as regression analysis or time series analysis to predict the missing value.
3. Validate the model by checking its performance on known data.

Gallery of Missing Number Patterns

Missing Number Patterns Image Gallery

Frequently Asked Questions

What is the difference between an arithmetic and a geometric sequence?

+

An arithmetic sequence has a constant difference between each consecutive term, while a geometric sequence has a constant ratio between each consecutive term.

How do I identify the pattern in a sequence?

+

Identifying the pattern involves examining the differences or ratios between consecutive terms and recognizing whether the sequence follows a known pattern such as arithmetic, geometric, or another type of sequence.

What if the sequence does not follow a simple arithmetic or geometric pattern?

+

In such cases, more complex patterns or sequences may be involved, requiring the use of algebraic methods, pattern recognition techniques, or statistical analysis to identify and predict the missing term.

Finding missing numbers in sequences and patterns is a fundamental skill that has numerous applications in mathematics, science, and everyday problem-solving. By understanding the different types of sequences, recognizing patterns, and applying appropriate methods, one can efficiently identify and fill in missing values. Whether dealing with simple arithmetic sequences or more complex patterns, the ability to analyze and complete sequences is an essential tool for anyone looking to improve their mathematical and analytical skills. We invite you to share your thoughts, ask questions, or provide examples of sequences and patterns you've encountered, and don't forget to share this article with others who might find it helpful.