5 Ways To Get P Value

Understanding the concept of p-value is crucial in statistical analysis as it helps researchers determine the significance of their findings. The p-value, or probability value, is a key component in hypothesis testing, indicating the probability of observing results at least as extreme as those observed, assuming that the null hypothesis is true. Here are five ways to get the p-value, each with its own application and relevance in different statistical contexts.

The importance of p-value cannot be overstated. It is a measure that helps in making informed decisions about whether the results of a study are due to chance or if they reflect a real effect. With the increasing reliance on data-driven insights across various fields, from healthcare and social sciences to finance and technology, understanding how to calculate and interpret p-values is essential.

Moreover, the calculation of p-values is not a one-size-fits-all approach. Different statistical tests and software packages provide various methods for obtaining p-values, depending on the nature of the data and the research question at hand. This flexibility is both a strength and a challenge, as it requires researchers to have a good grasp of statistical principles and the assumptions underlying different tests.

Introduction to P-Value Calculation

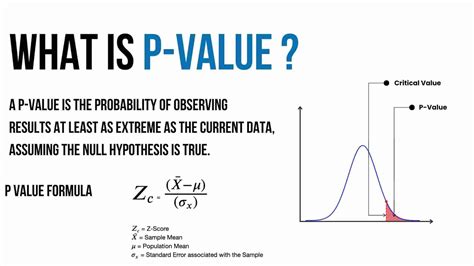
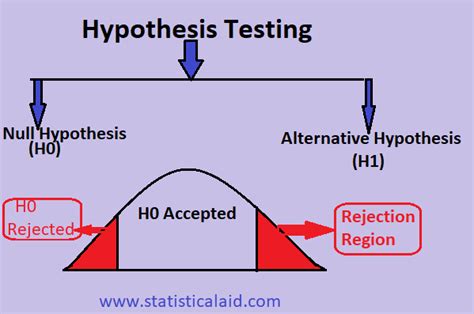
The calculation of a p-value is fundamentally about assessing the probability of observing a certain result, or more extreme, given a null hypothesis. The null hypothesis typically represents a statement of no effect or no difference. For instance, in a medical study, the null hypothesis might state that a new drug has no effect on a particular condition. The alternative hypothesis, on the other hand, suggests that there is an effect or difference, such as the drug having a significant impact on the condition.

Method 1: Using Statistical Software

One of the most common and efficient ways to obtain a p-value is by using statistical software. Packages like R, SPSS, SAS, and Python libraries such as SciPy and Statsmodels offer a wide range of statistical tests that automatically calculate p-values. For example, in R, the t.test() function for a t-test or the lm() function for linear regression analysis will output the p-value along with other test statistics. This method is not only time-saving but also reduces the chance of human error in calculations.

Steps for Using Statistical Software

• Data Preparation: Ensure your data is clean, and variables are appropriately defined.
• Selecting the Test: Choose the statistical test that aligns with your research question and data type.
• Interpreting Results: Look for the p-value in the output and compare it with your chosen significance level (usually 0.05) to decide whether to reject the null hypothesis.

Method 2: Manual Calculation

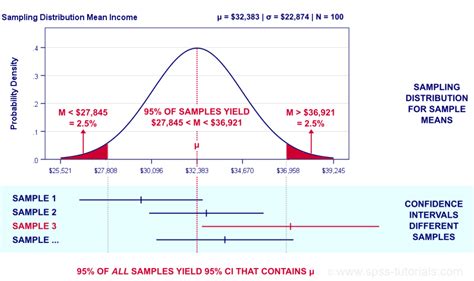
For educational purposes or when working with simple datasets, manually calculating the p-value can be instructive. This involves calculating the test statistic and then finding the probability of observing this statistic (or a more extreme one) under the null hypothesis. For instance, in a z-test or t-test, you would calculate the z-score or t-score and then use a standard normal distribution table or t-distribution table to find the corresponding p-value.

Benefits of Manual Calculation

• Understanding: It helps in understanding the underlying statistical concepts.
• Precision: For small datasets, it can provide a precise calculation of the p-value.
• Educational: It is a valuable learning tool for students of statistics.

Method 3: Simulation Studies

Simulation studies involve generating data under the null hypothesis and then calculating the test statistic for each simulated dataset. By repeating this process many times, you can estimate the p-value as the proportion of times the test statistic is at least as extreme as the one observed in your actual data. This method is particularly useful for complex data structures or when traditional statistical tests are not applicable.

Advantages of Simulation Studies

• Flexibility: Can be adapted to various research scenarios.
• Accuracy: Provides accurate estimates of p-values, especially in non-standard situations.
• Robustness: Can be used to validate the results of other statistical methods.

Method 4: Bootstrap Sampling

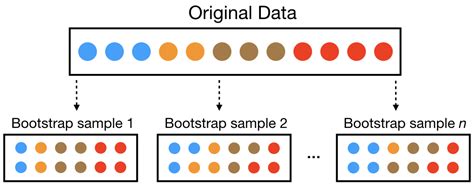
Bootstrap sampling is a resampling method that involves repeatedly sampling with replacement from the original dataset to generate new samples. For each bootstrap sample, the test statistic is calculated, and the distribution of these statistics across all bootstrap samples can be used to estimate the p-value. This method is useful for constructing confidence intervals and can also be applied to estimate p-values in certain scenarios.

Bootstrap Sampling Steps

• Resampling: Generate bootstrap samples from your original dataset.
• Calculate Test Statistic: For each bootstrap sample, calculate the relevant test statistic.
• Estimate P-Value: Use the distribution of test statistics to estimate the p-value.

Method 5: Approximations and Asymptotic Methods

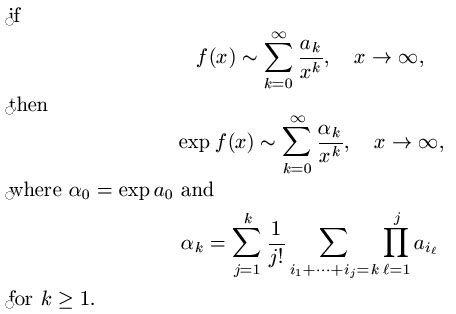
For large sample sizes, asymptotic methods can be used to approximate the distribution of the test statistic under the null hypothesis. These methods are based on the theory that as the sample size increases, the distribution of certain statistics approaches a known distribution (e.g., normal distribution). This allows for the calculation of approximate p-values, which can be particularly useful in situations where exact methods are computationally intensive or not available.

Advantages of Asymptotic Methods

• Efficiency: Can be computationally more efficient than exact methods.
• Applicability: Useful for large datasets where exact calculations might be impractical.
• Accuracy: Provides accurate approximations for p-values in many cases.

P-Value Calculation Methods Gallery

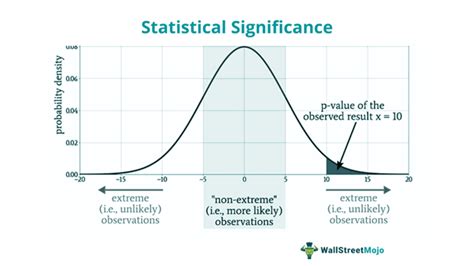
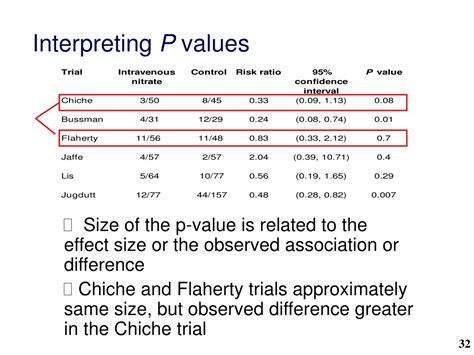
What is the purpose of calculating the p-value in statistical analysis?

+

The p-value helps determine the significance of the results, indicating whether the observed effects are likely due to chance or if they reflect a real phenomenon.

How do I choose the appropriate method for calculating the p-value?

+

The choice of method depends on the research question, data type, sample size, and the assumptions of the statistical test. For instance, simulation studies might be preferred for complex data structures, while asymptotic methods could be suitable for large sample sizes.

What are some common misconceptions about p-values that researchers should be aware of?

+

Common misconceptions include equating the p-value with the probability of the null hypothesis being true, misunderstanding the p-value as the probability of replicating the findings, and failing to consider the limitations and assumptions of the statistical test used to calculate the p-value.

In conclusion, the calculation and interpretation of p-values are critical components of statistical analysis, allowing researchers to make informed decisions about their findings. By understanding the different methods available for calculating p-values and their appropriate applications, researchers can enhance the validity and reliability of their studies. Whether through statistical software, manual calculations, simulation studies, bootstrap sampling, or asymptotic methods, the accurate determination of p-values is essential for advancing knowledge in various fields. As such, it is crucial for researchers to be well-versed in these methods and to approach p-value interpretation with a nuanced understanding of its implications and limitations. We invite readers to share their insights and experiences with calculating and interpreting p-values, and to explore the resources and references provided for further learning.