Intro
Understanding statistical analysis is crucial in various fields, including social sciences, medicine, and economics. One of the key statistical methods used to measure the strength and direction of the relationship between two variables is the Spearman correlation. This non-parametric test is particularly useful when dealing with data that doesn't follow a normal distribution or when the data is ordinal. In this article, we will delve into the world of Spearman correlation, exploring its importance, how it works, and practical examples of its application.
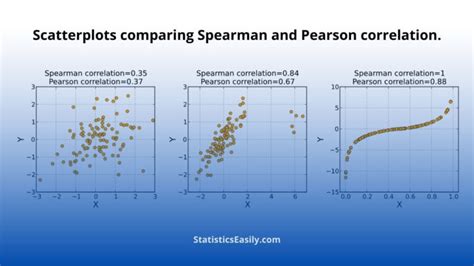
The Spearman correlation coefficient, often denoted as ρ (rho), ranges from -1 to 1, where 1 indicates a perfect positive correlation, -1 indicates a perfect negative correlation, and 0 suggests no correlation. This method is named after Charles Spearman, who developed it in the early 20th century as a non-parametric alternative to Pearson's correlation coefficient, which requires data to be normally distributed.
Spearman correlation is widely used due to its simplicity and the fact that it can handle data that is not normally distributed. It calculates the correlation between the ranks of two variables, making it particularly useful for ordinal data or when the relationship between variables is not linear.
What is Spearman Correlation?
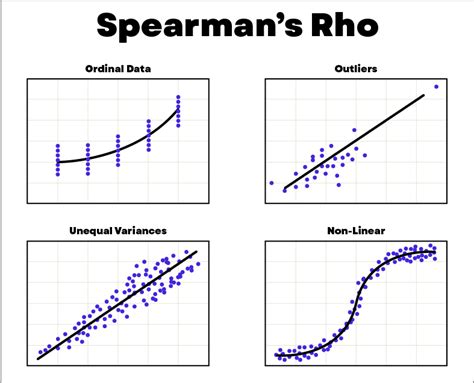
Spearman correlation is a statistical method used to assess the relationship between two variables. It is based on the ranked values of the data rather than the actual values, which makes it robust against outliers and suitable for data that does not meet the assumptions of parametric tests.
Key Characteristics of Spearman Correlation
The key characteristics of Spearman correlation include: - **Non-parametric**: It does not require the data to follow a specific distribution, making it versatile. - **Robust to Outliers**: Because it uses ranks, extreme values have less impact on the correlation coefficient. - **Ordinal Data**: It is particularly useful for analyzing ordinal data, where the data can be ranked but not necessarily measured on a continuous scale.How Does Spearman Correlation Work?
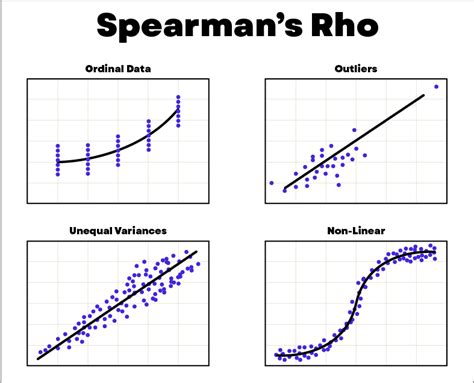
The calculation of Spearman correlation involves ranking the data for each variable and then comparing these ranks. The formula for Spearman correlation coefficient (ρ) is: [ \rho = 1 - \frac{6 \sum d^2}{n(n^2 - 1)} ] where (d) is the difference between the ranks of the two variables for each observation, and (n) is the number of observations.
Steps to Calculate Spearman Correlation
Calculating Spearman correlation involves the following steps: 1. **Rank the Data**: Rank each variable separately. 2. **Calculate Differences**: Calculate the difference in ranks for each pair of observations. 3. **Square the Differences**: Square each of these differences. 4. **Sum the Squares**: Sum up these squared differences. 5. **Apply the Formula**: Plug the sum of squared differences and the number of observations into the Spearman correlation formula.Practical Applications of Spearman Correlation
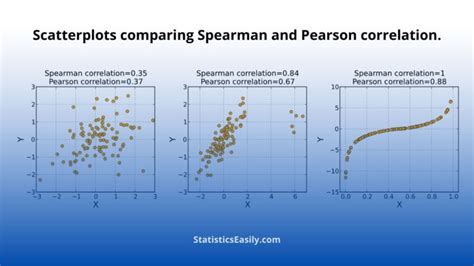
Spearman correlation has numerous practical applications across various fields:
- Social Sciences: To study the relationship between attitudes, behaviors, and demographic variables.
- Medicine: To analyze the relationship between the severity of symptoms and treatment outcomes.
- Economics: To examine the relationship between economic indicators, such as GDP and inflation rates.
Examples of Spearman Correlation in Real-World Scenarios
- **Education**: A researcher might use Spearman correlation to investigate the relationship between students' ranks in a class and their scores on a standardized test. - **Psychology**: To study the correlation between the rank of anxiety levels (as reported by patients) and the rank of their performance in a stress-inducing task.Interpretation of Spearman Correlation Coefficient
Interpreting the Spearman correlation coefficient involves understanding its value and significance:
- Value: Ranges from -1 to 1, where 1 is a perfect positive correlation, -1 is a perfect negative correlation, and 0 indicates no correlation.
- Significance: Often tested using a t-test to determine if the observed correlation is statistically significant, meaning it is unlikely to occur by chance.
Guidelines for Interpretation
- **Strength of Correlation**: The closer the coefficient is to 1 or -1, the stronger the correlation. - **Direction of Correlation**: A positive coefficient indicates that as one variable increases, the other tends to increase. A negative coefficient indicates that as one variable increases, the other tends to decrease.Limitations and Considerations

While Spearman correlation is a powerful tool, it has its limitations:
- Assumes Monotonic Relationship: It assumes that the relationship between the variables is monotonic (either consistently increasing or consistently decreasing), which might not always be the case.
- Sensitive to Ties: The presence of tied ranks can affect the calculation, especially if there are many ties.
Addressing Limitations
- **Check for Monotonicity**: Before applying Spearman correlation, ensure that the relationship between the variables appears to be monotonic. - **Alternative Methods**: Consider alternative non-parametric correlation coefficients, such as Kendall's tau, which can handle ties and non-monotonic relationships differently.Spearman Correlation Image Gallery
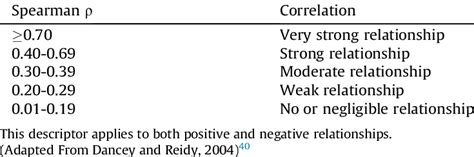
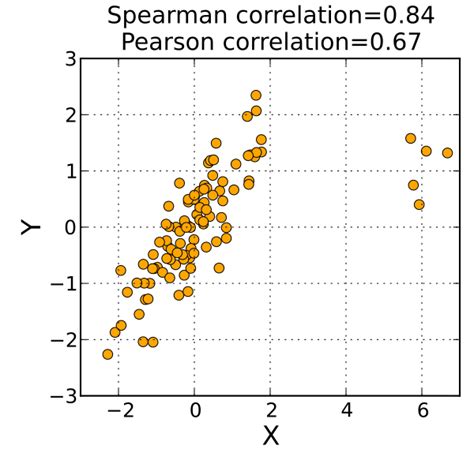
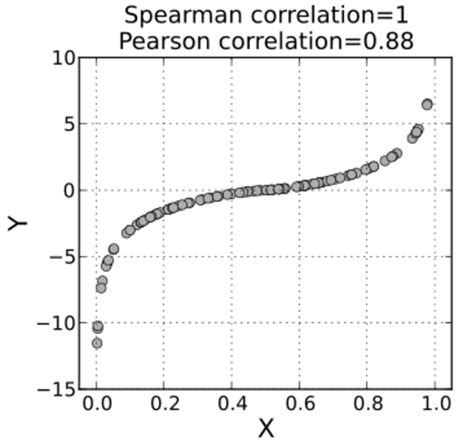
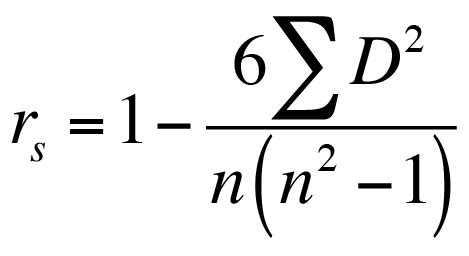
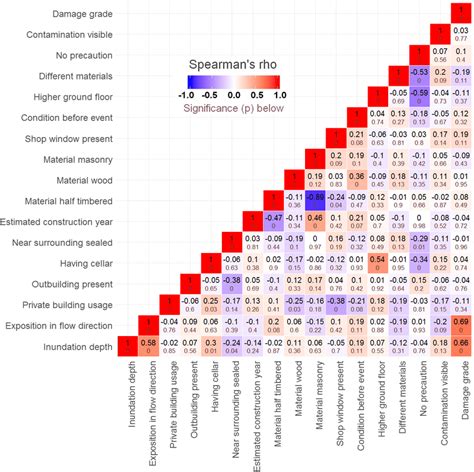
What is the main advantage of using Spearman correlation?
+The main advantage of using Spearman correlation is its ability to handle non-normal data and its robustness against outliers, making it a versatile statistical tool.
How does Spearman correlation differ from Pearson correlation?
+Spearman correlation differs from Pearson correlation in that it uses ranks rather than actual values, making it suitable for non-parametric data and more robust against outliers.
What does a Spearman correlation coefficient of 0.7 indicate?
+A Spearman correlation coefficient of 0.7 indicates a strong positive correlation between the two variables, meaning as one variable increases, the other tends to increase as well.
In conclusion, Spearman correlation is a powerful statistical tool for analyzing the relationship between two variables, especially when the data does not meet the assumptions of parametric tests. Its ability to handle non-normal data and its robustness against outliers make it a preferred choice in many research scenarios. By understanding how to calculate and interpret Spearman correlation, researchers and analysts can uncover valuable insights into the relationships within their data, contributing to informed decision-making and further research. We invite you to share your thoughts on the applications and limitations of Spearman correlation in the comments below and to explore more statistical analysis techniques to deepen your understanding of data analysis.