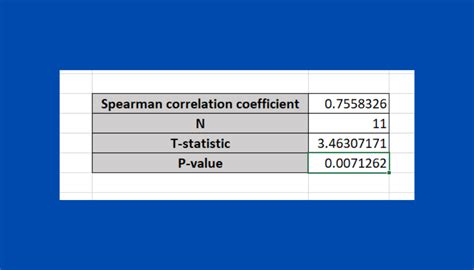
Spearman Rank Correlation In Excel

Spearman rank correlation is a statistical method used to measure the strength and direction of the relationship between two variables. It is a non-parametric test, which means it doesn't require the data to follow a specific distribution. In Excel, you can calculate the Spearman rank correlation using the CORREL function or by using the Analysis ToolPak add-in.

The importance of understanding the relationship between variables cannot be overstated. In various fields such as finance, marketing, and social sciences, identifying correlations can help in making informed decisions, predicting outcomes, and understanding the underlying dynamics of a system. The Spearman rank correlation is particularly useful when dealing with ordinal data or when the relationship between variables is not linear.

To entice readers to continue reading, let's consider a practical example. Suppose you are a marketing manager and want to understand the relationship between the price of a product and its sales. You collect data on the prices of different products and their corresponding sales figures. By applying the Spearman rank correlation, you can determine if there is a significant relationship between the price and sales, which can inform your pricing strategy.

Introduction to Spearman Rank Correlation

The Spearman rank correlation coefficient (ρ) measures the strength and direction of the association between two ranked variables. The coefficient ranges from -1 to 1, where: - 1 indicates a perfect positive correlation, - -1 indicates a perfect negative correlation, - 0 indicates no correlation.

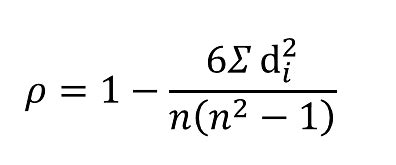
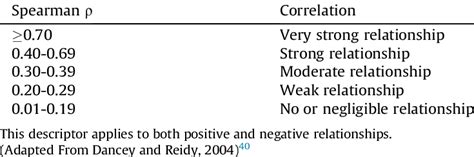
Interpretation of Spearman Rank Correlation Coefficient

The interpretation of the Spearman rank correlation coefficient is as follows: - A coefficient close to 1 or -1 indicates a strong correlation. - A coefficient close to 0 indicates a weak correlation. - The sign of the coefficient indicates the direction of the relationship: positive for direct relationships and negative for inverse relationships.

Calculating Spearman Rank Correlation in Excel

To calculate the Spearman rank correlation in Excel, you can use the CORREL function. However, this function calculates the Pearson correlation coefficient, which is a different measure. For Spearman rank correlation, you can use the following steps:

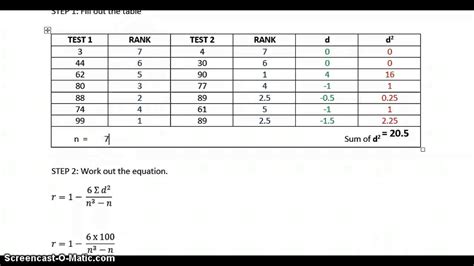
Rank your data: Use the RANK.AVG function to assign ranks to your data.
Calculate the difference between the ranks: Calculate the difference between the ranks of the two variables for each observation.
Calculate the Spearman rank correlation coefficient: Use the formula for the Spearman rank correlation coefficient, which involves the sum of the squared differences between the ranks.

Alternatively, you can use the Analysis ToolPak add-in in Excel, which provides a built-in function for calculating the Spearman rank correlation.

Using Analysis ToolPak for Spearman Rank Correlation

To use the Analysis ToolPak for Spearman rank correlation: 1. Install the Analysis ToolPak add-in if it's not already installed. 2. Select the data range for the two variables. 3. Go to the "Data" tab and click on "Data Analysis". 4. Select "Correlation" from the list of available tools. 5. Check the box for "Spearman" and click "OK".

Practical Examples of Spearman Rank Correlation

Let's consider a few practical examples of using Spearman rank correlation: - Analyzing the relationship between student rankings and their scores on a standardized test. - Examining the correlation between the ranking of movies based on their box office performance and their ranking based on critical reviews. - Investigating the relationship between the ranking of athletes based on their performance in one event and their ranking in another event.

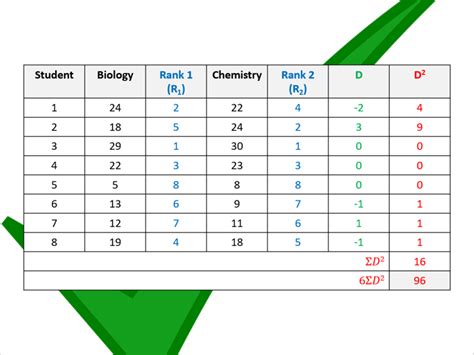
These examples illustrate how the Spearman rank correlation can be applied in various contexts to understand the relationships between ranked variables.

Advantages and Limitations of Spearman Rank Correlation

The advantages of Spearman rank correlation include: - It is a non-parametric test, which means it doesn't require the data to follow a specific distribution. - It is robust to outliers. - It can handle ordinal data.

However, the limitations include:

It assumes that the data are continuous or at least ordinal.
It may not be as powerful as parametric tests when the data are normally distributed.

Gallery of Spearman Rank Correlation

Spearman Rank Correlation Image Gallery

Interpretation of Spearman Rank Correlation

Limitations of Spearman Rank Correlation

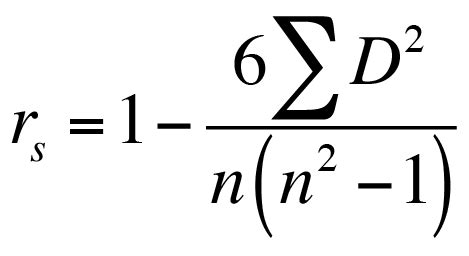
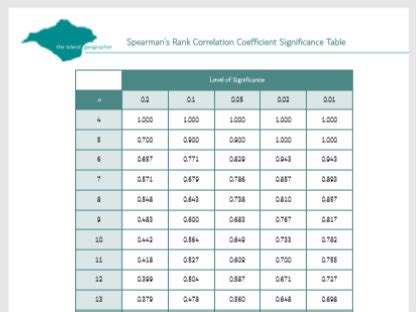
What is the Spearman rank correlation coefficient?

The Spearman rank correlation coefficient is a statistical measure that calculates the strength and direction of the relationship between two ranked variables.

How do I calculate the Spearman rank correlation in Excel?

You can calculate the Spearman rank correlation in Excel using the CORREL function or by using the Analysis ToolPak add-in.

What are the advantages and limitations of the Spearman rank correlation?

The advantages of the Spearman rank correlation include being a non-parametric test and robust to outliers. The limitations include assuming continuous or ordinal data and potentially being less powerful than parametric tests for normally distributed data.

In conclusion, the Spearman rank correlation is a valuable statistical tool for understanding the relationships between ranked variables. By following the steps outlined in this article, you can calculate the Spearman rank correlation in Excel and apply it to various practical examples. We invite you to share your experiences with using the Spearman rank correlation and to ask any questions you may have about this topic. Additionally, we encourage you to explore other statistical methods and tools to further enhance your data analysis skills.