Intro
Calculate volumes of irregular figures with ease using our worksheet, covering complex shapes and 3D geometry, including surface area and volume formulas for precise calculations.
The concept of calculating the volume of irregular figures is a fundamental aspect of geometry and mathematics. Understanding how to determine the volume of such figures is crucial for various applications in physics, engineering, and architecture. In this article, we will delve into the importance of calculating volumes, the challenges associated with irregular figures, and provide a comprehensive guide on how to approach these calculations.
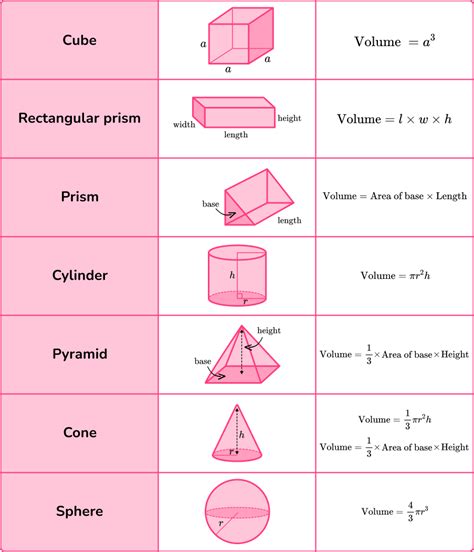
Calculating the volume of regular geometric shapes like cubes, spheres, and cylinders is straightforward due to their symmetrical and predictable structures. However, irregular figures pose a significant challenge due to their unique and often complex shapes. The volume of an irregular figure can be approximated or calculated using various methods, depending on the figure's complexity and the available data.
Introduction to Volume Calculations
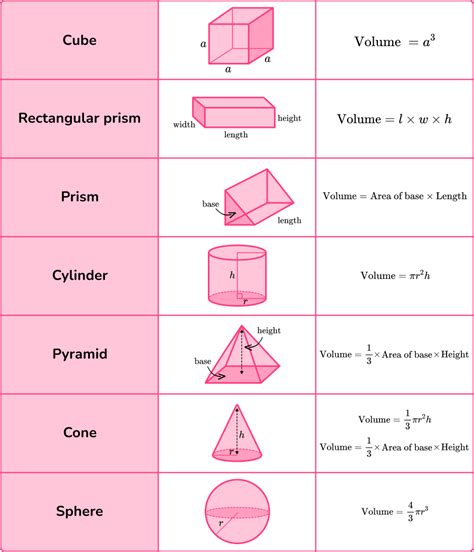
Volume calculations are essential in various fields, including construction, where architects need to calculate the volume of buildings and other structures to determine the amount of materials required. In physics, understanding volumes is critical for calculating densities and buoyancies. The method of calculating the volume depends on the shape and the information available about the shape.
Understanding Irregular Figures

Irregular figures are those that do not conform to the standard geometric shapes. They can be found in nature, such as the shape of rocks or the irregular contours of landscapes, or they can be man-made, like certain architectural designs. The challenge with irregular figures is that they do not fit into the simple formulas used for regular shapes, requiring more complex methods for volume calculation.
Methods for Calculating Volume
There are several methods to calculate the volume of irregular figures, including: - **Dissection Method**: This involves breaking down the irregular figure into simpler shapes whose volumes can be easily calculated. - **Integration Method**: Used for more complex shapes, this method involves using calculus to sum up the volumes of infinitesimally small parts of the figure. - **Approximation Methods**: These involve using known volumes of similar shapes or parts of the shape to estimate the total volume.Practical Applications

The ability to calculate the volume of irregular figures has numerous practical applications. In engineering, it's crucial for designing storage tanks, pipelines, and other containers. In environmental science, understanding the volume of irregularly shaped bodies of water or land formations is essential for studies on ecology and conservation.
Steps for Calculation
Calculating the volume of an irregular figure involves several steps: 1. **Data Collection**: Gather as much information as possible about the dimensions and shape of the figure. 2. **Dissection**: If possible, dissect the figure into simpler shapes. 3. **Apply Formulas**: Use known volume formulas for the simpler shapes. 4. **Integration or Approximation**: If the figure cannot be dissected into simpler shapes, use integration or approximation methods.Challenges and Considerations

One of the main challenges in calculating the volume of irregular figures is the complexity of their shapes. This complexity can make it difficult to apply standard formulas directly. Additionally, the accuracy of the calculation can depend heavily on the method used and the precision of the measurements taken.
Solutions and Tools
Several tools and software are available to aid in the calculation of volumes of irregular figures, including: - **CAD Software**: Computer-aided design software can be used to create models of irregular figures and calculate their volumes. - **Mathematical Software**: Programs like Mathematica or MATLAB can be used to perform complex calculations, including integrations.Gallery of Volume Calculations
Volume Calculations Image Gallery



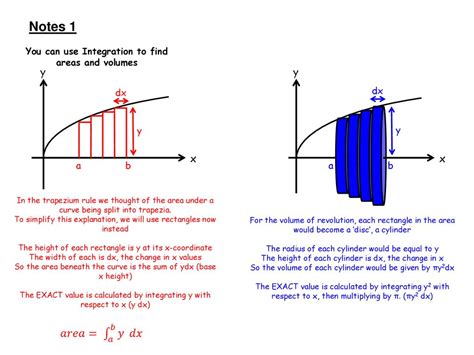
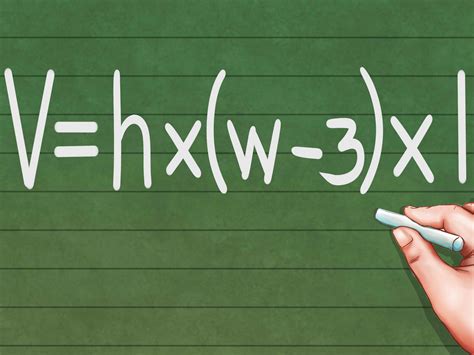

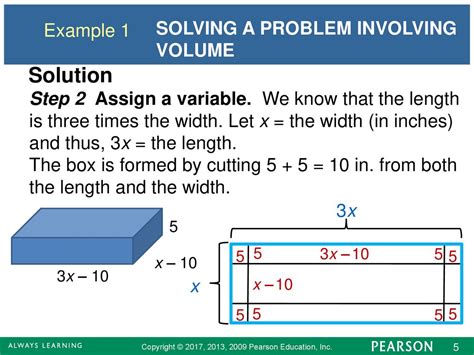
Frequently Asked Questions
What is the importance of calculating the volume of irregular figures?
+Calculating the volume of irregular figures is crucial for various applications in physics, engineering, and architecture, including designing structures, calculating densities, and determining material quantities.
What methods are used to calculate the volume of irregular figures?
+The methods include dissection into simpler shapes, integration, and approximation methods. The choice of method depends on the complexity of the figure and the available data.
What tools are available to aid in volume calculations?
+Several tools and software are available, including CAD software for modeling and mathematical software like Mathematica or MATLAB for complex calculations.
In conclusion, calculating the volume of irregular figures is a complex task that requires a deep understanding of geometry and mathematics. With the right approach and tools, individuals can accurately determine the volumes of these figures, which is essential for various practical applications. We invite readers to share their experiences and challenges with volume calculations, and we hope this article has provided valuable insights and guidance on this topic. Whether you're a student, engineer, or simply someone interested in mathematics, understanding how to calculate the volume of irregular figures can open up new avenues of knowledge and application.