Intro
Discover 5 ways to calculate rate, including formula methods, proportion techniques, and ratio calculations, to improve math skills and solve problems efficiently with rate conversion and calculation strategies.
Calculating rates is a fundamental concept in various fields, including mathematics, physics, economics, and finance. Understanding how to calculate rates is essential for making informed decisions, predicting outcomes, and analyzing data. In this article, we will explore five ways to calculate rates, providing examples and explanations to help you grasp these concepts.
The importance of calculating rates cannot be overstated. Rates are used to measure the speed at which something changes, grows, or decreases. They help us understand the relationship between different variables, make predictions, and identify trends. Whether you're a student, a professional, or simply someone interested in learning, mastering the art of calculating rates is a valuable skill.
In today's fast-paced world, calculating rates is more crucial than ever. With the vast amount of data available, being able to analyze and interpret rates is essential for making informed decisions. From calculating interest rates on investments to determining the rate of change in a company's stock price, understanding rates is vital for success. In this article, we will delve into five ways to calculate rates, providing you with a comprehensive understanding of this concept.
Introduction to Calculating Rates
Calculating rates involves determining the ratio of change between two variables. This can be done using various formulas and techniques, depending on the context and the type of data being analyzed. The five ways to calculate rates that we will explore in this article include the simple interest rate, the compound interest rate, the rate of change, the average rate, and the marginal rate.
Simple Interest Rate

The simple interest rate is a basic concept in finance that calculates the interest earned on an investment or loan. It is calculated by multiplying the principal amount by the interest rate and the time period. The formula for simple interest is:
Simple Interest = Principal x Rate x Time
For example, if you invest $1,000 at a 5% interest rate for 2 years, the simple interest would be:
Simple Interest = $1,000 x 0.05 x 2 = $100
Example of Simple Interest Rate
The simple interest rate is commonly used in savings accounts, certificates of deposit, and other types of investments. It provides a straightforward way to calculate the interest earned on an investment, making it easy to compare different options.Compound Interest Rate

The compound interest rate is a more complex concept that calculates the interest earned on an investment or loan, taking into account the compounding effect. It is calculated by multiplying the principal amount by the interest rate and the time period, and then adding the interest earned in previous periods. The formula for compound interest is:
Compound Interest = Principal x (1 + Rate)^Time - Principal
For example, if you invest $1,000 at a 5% interest rate for 2 years, compounded annually, the compound interest would be:
Compound Interest = $1,000 x (1 + 0.05)^2 - $1,000 = $102.50
Example of Compound Interest Rate
The compound interest rate is commonly used in investments such as stocks, bonds, and mutual funds. It provides a more accurate picture of the interest earned on an investment, taking into account the compounding effect.Rate of Change
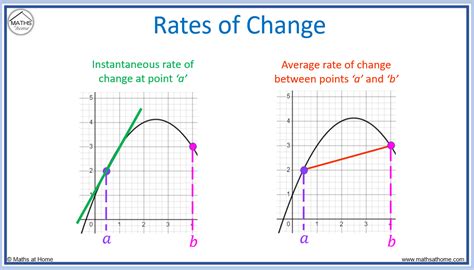
The rate of change is a concept in mathematics that calculates the ratio of change between two variables. It is calculated by dividing the change in the dependent variable by the change in the independent variable. The formula for the rate of change is:
Rate of Change = (Change in Dependent Variable) / (Change in Independent Variable)
For example, if the price of a stock increases from $50 to $75 over a period of 6 months, the rate of change would be:
Rate of Change = ($75 - $50) / 6 = $4.17 per month
Example of Rate of Change
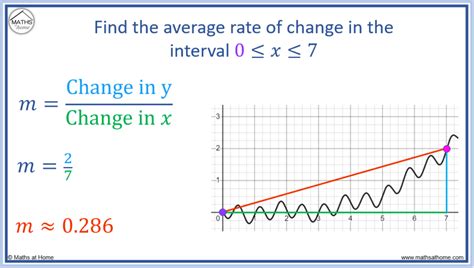
The rate of change is commonly used in physics, engineering, and economics to analyze the relationship between different variables. It provides a way to measure the speed at which something changes, making it essential for predicting outcomes and identifying trends.Average Rate
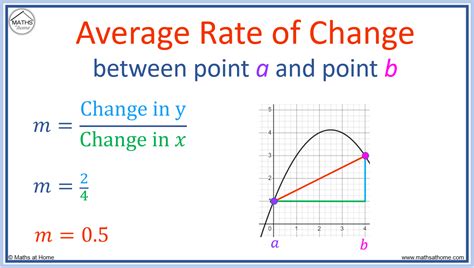
The average rate is a concept in statistics that calculates the mean rate of change over a period of time. It is calculated by summing up the rates of change over different periods and dividing by the number of periods. The formula for the average rate is:
Average Rate = (Sum of Rates) / (Number of Periods)
For example, if the rate of change of a stock price is 5% in the first quarter, 3% in the second quarter, and 7% in the third quarter, the average rate would be:
Average Rate = (5% + 3% + 7%) / 3 = 5% per quarter
Example of Average Rate
The average rate is commonly used in finance and economics to analyze the performance of investments and predict future trends. It provides a way to smooth out fluctuations and identify the underlying trend.Marginal Rate
The marginal rate is a concept in economics that calculates the rate of change of a variable with respect to a small change in another variable. It is calculated by dividing the change in the dependent variable by the change in the independent variable, while keeping all other variables constant. The formula for the marginal rate is:
Marginal Rate = (Change in Dependent Variable) / (Change in Independent Variable)
For example, if the demand for a product increases by 10 units when the price decreases by $1, the marginal rate would be:
Marginal Rate = 10 units / $1 = 10 units per dollar
Example of Marginal Rate
The marginal rate is commonly used in microeconomics to analyze the behavior of consumers and firms. It provides a way to measure the responsiveness of a variable to a small change in another variable, making it essential for predicting outcomes and identifying trends.Rate Calculation Image Gallery





What is the difference between simple interest and compound interest?
+Simple interest calculates the interest earned on an investment or loan, while compound interest takes into account the compounding effect, where interest is earned on both the principal and the interest.
How do I calculate the rate of change?
+The rate of change is calculated by dividing the change in the dependent variable by the change in the independent variable.
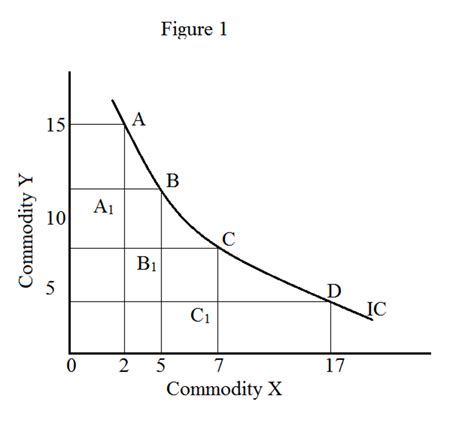
What is the marginal rate of substitution?
+The marginal rate of substitution is the rate at which a consumer is willing to substitute one good for another, while keeping the level of satisfaction constant.
In conclusion, calculating rates is a fundamental concept that has numerous applications in various fields. By understanding the different ways to calculate rates, including simple interest, compound interest, rate of change, average rate, and marginal rate, you can make informed decisions, predict outcomes, and analyze data. Whether you're a student, a professional, or simply someone interested in learning, mastering the art of calculating rates is a valuable skill that can benefit you in many ways. We hope this article has provided you with a comprehensive understanding of this concept, and we encourage you to share your thoughts and questions in the comments below.