Payback Period Formula In Excel

The payback period is a crucial financial metric used to evaluate the feasibility of a project or investment. It represents the amount of time required for an investment to generate returns equal to its initial cost. In other words, it's the time it takes for an investor to recoup their investment. Calculating the payback period in Excel is a straightforward process that can be accomplished using a simple formula. In this article, we will delve into the world of payback period calculations, exploring the formula, its application in Excel, and providing examples to illustrate its usage.

To understand the importance of the payback period, consider a scenario where you're deciding between two investments. Both have the potential to yield significant returns, but one requires a larger upfront investment. By calculating the payback period, you can determine which investment is likely to generate returns more quickly, helping you make a more informed decision. The payback period is particularly useful for evaluating investments with different cash flow patterns, as it provides a clear indication of when you can expect to break even.

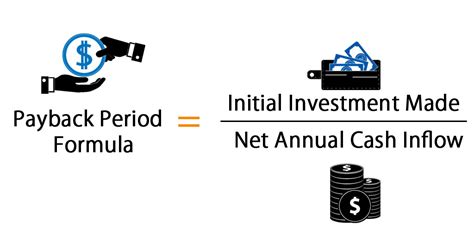
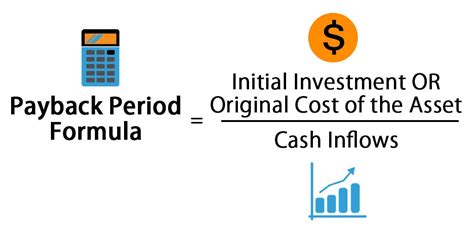
The payback period formula is relatively simple: Payback Period = Initial Investment / Annual Cash Flow. However, this basic formula assumes that the annual cash flow is constant, which might not always be the case. For investments with varying annual cash flows, a more detailed approach is necessary, involving the cumulative cash flow over the years until it equals or exceeds the initial investment. Excel provides an efficient way to calculate the payback period for both scenarios, using formulas and functions that can handle complex cash flow patterns.

Understanding the Payback Period Formula

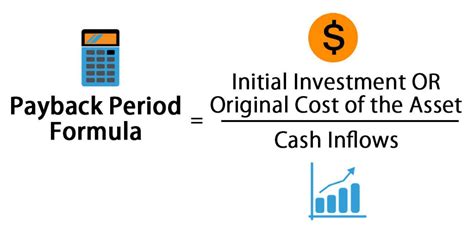
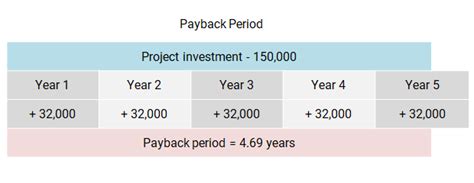
The payback period formula, in its simplest form, is calculated by dividing the initial investment by the annual cash inflow. This method is useful for projects with uniform annual returns. For instance, if you invest $100,000 in a project that generates $20,000 in cash flow each year, the payback period would be $100,000 / $20,000 = 5 years. However, many investments have varying annual cash flows, making it necessary to calculate the cumulative cash flow for each year until the total equals or exceeds the initial investment.

Calculating Payback Period with Uniform Annual Cash Flows

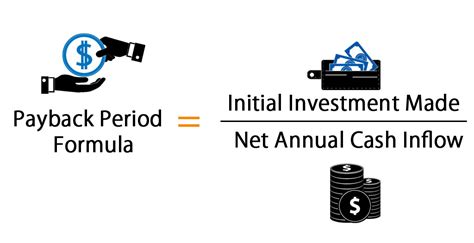
For investments with consistent annual cash flows, the payback period calculation is straightforward. You simply divide the initial investment by the annual cash flow. This can be represented in Excel using a simple division formula. For example, if the initial investment is in cell A1 and the annual cash flow is in cell B1, the payback period formula would be =A1/B1.

Using Excel for Payback Period Calculations

Excel offers a powerful platform for calculating the payback period, especially for investments with non-uniform cash flows. By listing the annual cash flows in a column, you can calculate the cumulative cash flow in an adjacent column. The payback period is then determined by identifying the year in which the cumulative cash flow first equals or exceeds the initial investment. Excel's NPV (Net Present Value) and IRR (Internal Rate of Return) functions can also be used in conjunction with payback period calculations to provide a more comprehensive analysis of an investment's viability.

Calculating Payback Period with Non-Uniform Annual Cash Flows in Excel

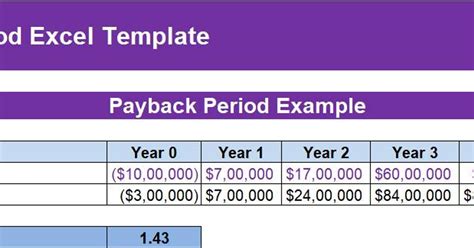
For projects with varying annual cash flows, you can calculate the payback period in Excel by following these steps: 1. List the annual cash flows in a column. 2. Calculate the cumulative cash flow in an adjacent column. 3. Use the formula to find the year when the cumulative cash flow equals or exceeds the initial investment.

This approach can be illustrated with an example where an initial investment of $100,000 generates cash flows of $15,000, $25,000, $30,000, and $40,000 over four years. By calculating the cumulative cash flow for each year, you can determine the payback period.

Example Calculation

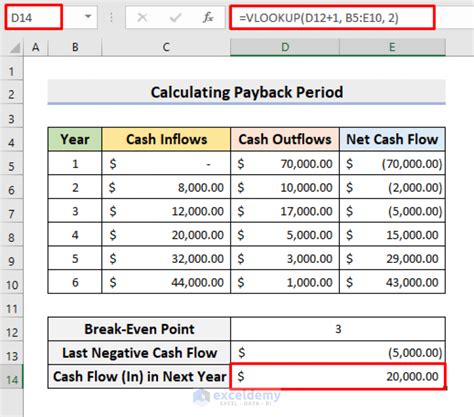
Let's consider an investment with the following annual cash flows: Year 1 = $10,000, Year 2 = $20,000, Year 3 = $30,000, and Year 4 = $40,000, with an initial investment of $80,000. The cumulative cash flows would be calculated as follows:

• Year 1: $10,000
• Year 2: $10,000 + $20,000 = $30,000
• Year 3: $30,000 + $30,000 = $60,000
• Year 4: $60,000 + $40,000 = $100,000

From this calculation, it's evident that the payback period is between 3 and 4 years because the cumulative cash flow exceeds the initial investment of $80,000 in the fourth year.

Interpreting Payback Period Results

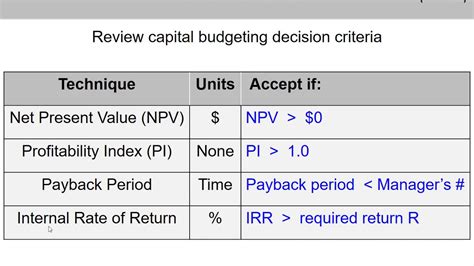
The payback period is a valuable metric for investors and businesses, as it provides insight into the liquidity of an investment. A shorter payback period indicates that an investment will generate returns more quickly, reducing the risk associated with the investment. However, it's essential to consider the payback period in conjunction with other financial metrics, such as the net present value (NPV) and internal rate of return (IRR), to get a comprehensive view of an investment's potential.

Limitations of the Payback Period

While the payback period is a useful tool for evaluating investments, it has several limitations. It does not account for the time value of money, meaning it treats cash flows received today the same as those received in the future. Additionally, it does not consider cash flows beyond the payback period, which can lead to overlooking investments with significant long-term potential. Therefore, it's crucial to use the payback period in conjunction with other financial analysis tools to make informed investment decisions.

Conclusion and Future Directions

In conclusion, the payback period is a fundamental concept in finance that helps investors and businesses evaluate the feasibility of projects and investments. By understanding how to calculate the payback period, both manually and using Excel, individuals can make more informed decisions about where to allocate their resources. As financial markets continue to evolve, the importance of thorough investment analysis will only grow, making the payback period an essential tool in the investor's toolkit.

Gallery of Payback Period Calculations

Payback Period Image Gallery

What is the payback period, and why is it important in finance?

+

The payback period is the time it takes for an investment to generate returns equal to its initial cost. It's crucial for evaluating the feasibility and risk of investments.

How do you calculate the payback period for an investment with uniform annual cash flows?

+

The payback period is calculated by dividing the initial investment by the annual cash flow.

What are the limitations of using the payback period for investment analysis?

+

The payback period does not account for the time value of money and does not consider cash flows beyond the payback period, which can lead to overlooking investments with significant long-term potential.

How can Excel be used to calculate the payback period for investments with non-uniform annual cash flows?

+

Excel can be used by listing the annual cash flows, calculating the cumulative cash flow, and identifying the year when the cumulative cash flow equals or exceeds the initial investment.

What other financial metrics should be considered alongside the payback period for comprehensive investment analysis?

+

Net Present Value (NPV) and Internal Rate of Return (IRR) are essential metrics that provide a more comprehensive view of an investment's potential and should be considered alongside the payback period.

We hope this comprehensive guide to the payback period formula in Excel has been informative and helpful. Whether you're an investor, a business owner, or simply looking to understand more about financial analysis, the payback period is a fundamental concept that can aid in making informed decisions. Feel free to share your thoughts, ask questions, or explore more topics related to finance and investment analysis in the comments below.