Intro
Learn 5 ways to create a bell curve, understanding normal distribution, data analysis, and statistical modeling to visualize skewed data, outliers, and probability density.
Understanding and creating a bell curve is essential in statistics and data analysis. A bell curve, also known as a normal distribution or Gaussian distribution, is a probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean. In this article, we will explore five ways to create a bell curve, including theoretical explanations, practical examples, and statistical software applications.
The bell curve is crucial because it helps in understanding the distribution of data in various fields, including social sciences, economics, and natural sciences. It is characterized by its bell-shaped curve, where the majority of data points cluster around the mean, and the probability of data points decreases as you move away from the mean. The creation and analysis of bell curves are fundamental skills for anyone working with data.
To delve into the specifics of creating a bell curve, it's essential to understand that there are multiple approaches, each suited to different contexts and requirements. Whether you're working with theoretical distributions, real-world data, or using statistical software, understanding how to generate and interpret bell curves is vital for data-driven insights.
Understanding the Basics of a Bell Curve
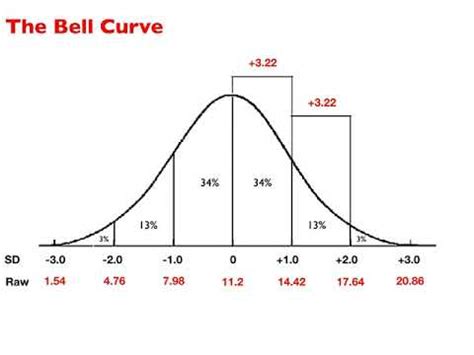
Before diving into the methods of creating a bell curve, it's essential to grasp the basics. A bell curve is defined by three main parameters: the mean (μ), which is the central tendency of the distribution; the standard deviation (σ), which measures the amount of variation or dispersion of a set of values; and the total area under the curve, which represents the total probability and is always equal to 1 in a probability distribution.
Theoretical Creation of a Bell Curve
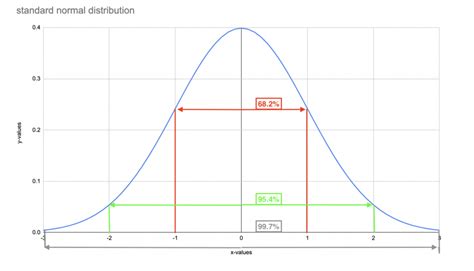
Theoretically, a bell curve can be created using the probability density function (PDF) of the normal distribution, which is given by the formula: f(x | μ, σ) = (1/σ√(2π)) * e^(-((x-μ)^2)/(2σ^2)). This formula allows you to calculate the probability density of any given value x, given the mean μ and standard deviation σ of the distribution.
Steps for Theoretical Creation
- Define the mean (μ) and standard deviation (σ) of your distribution.
- Use the PDF formula to calculate the probability density for a range of x values.
- Plot these x values against their corresponding probability densities to visualize the bell curve.
Practical Creation of a Bell Curve with Real Data

In practice, creating a bell curve involves analyzing real-world data to see if it follows a normal distribution. This can be done by collecting a dataset, calculating the mean and standard deviation, and then plotting a histogram of the data. If the data is normally distributed, the histogram will approximate a bell curve.
Steps for Practical Creation
- Collect a dataset relevant to your study or analysis.
- Calculate the mean and standard deviation of the dataset.
- Create a histogram of the data, with the x-axis representing the data values and the y-axis representing the frequency or density of these values.
- Compare the histogram to a bell curve to visually assess if the data is normally distributed.
Using Statistical Software to Create a Bell Curve
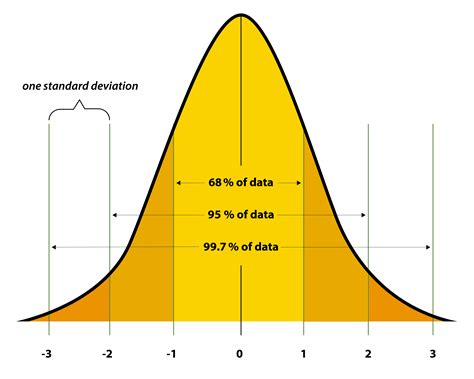
Statistical software packages such as R, Python libraries (e.g., NumPy, SciPy), and Excel can be used to create and analyze bell curves efficiently. These tools provide functions to calculate the mean, standard deviation, and to plot normal distributions, making it easier to work with bell curves.
Steps for Using Statistical Software
- Choose appropriate statistical software based on your familiarity and the complexity of the task.
- Input your data into the software or generate a theoretical dataset based on a normal distribution.
- Use built-in functions to calculate the mean and standard deviation of your data.
- Utilize plotting functions to visualize the bell curve.
Creating a Bell Curve for Specific Distributions
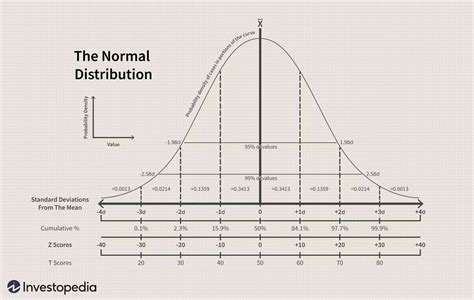
Sometimes, you might need to create a bell curve for specific distributions, such as a standard normal distribution (Z-distribution) where μ=0 and σ=1, or for distributions with specific mean and standard deviation values. This can be useful for comparing different datasets or for theoretical analyses.
Steps for Specific Distributions
- Define the parameters (mean and standard deviation) of the specific distribution you are interested in.
- Use these parameters in the PDF formula or in statistical software to generate the bell curve.
- Analyze and interpret the curve in the context of your study or application.
Visualizing and Interpreting Bell Curves
Visualizing and interpreting bell curves involve understanding the shape of the curve and what it tells you about the distribution of your data. A bell curve that is tall and narrow indicates that the data points tend to be close to the mean, while a short and wide curve indicates that the data points are spread out over a larger range of values.
Steps for Visualization and Interpretation
- Plot the bell curve using your chosen method.
- Observe the shape of the curve and note its characteristics, such as skewness and kurtosis.
- Interpret these characteristics in the context of your data and research questions.
Bell Curve Image Gallery
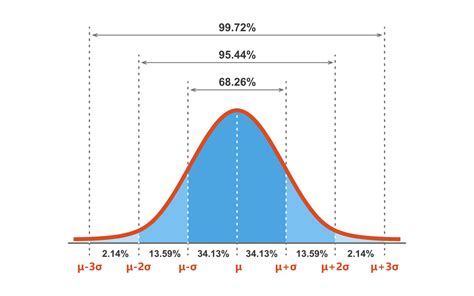
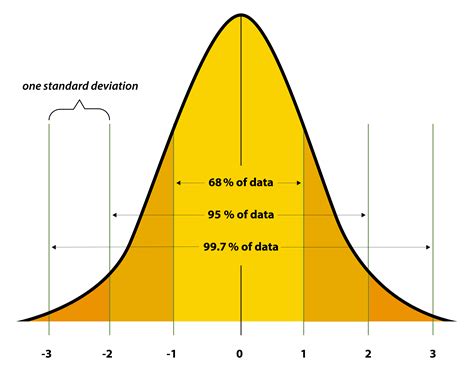


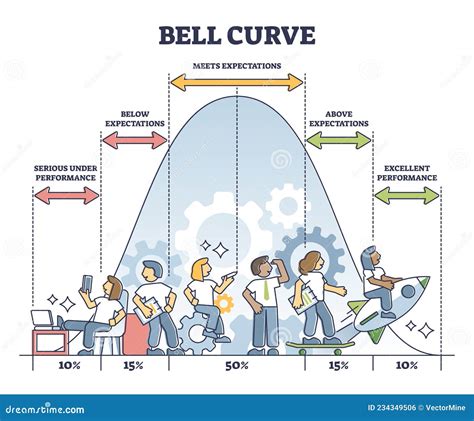
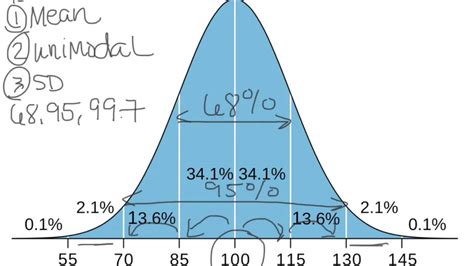
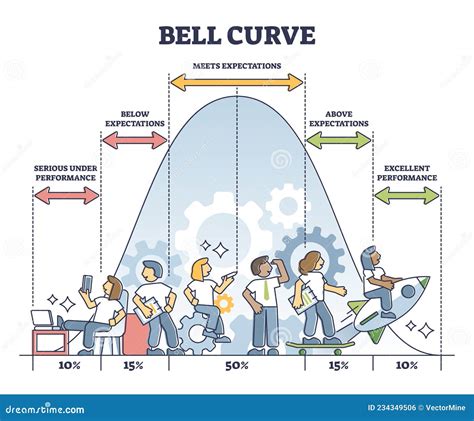
What is a bell curve and why is it important in statistics?
+A bell curve, or normal distribution, is a probability distribution that is symmetric about the mean, indicating that data near the mean are more frequent in occurrence than data far from the mean. It's crucial for understanding data distribution in various fields.
How do I determine if my data follows a normal distribution?
+To determine if your data follows a normal distribution, you can use statistical tests such as the Shapiro-Wilk test, visualize the data with a histogram or Q-Q plot, and calculate summary statistics like skewness and kurtosis.
What are the parameters that define a bell curve?
+A bell curve is defined by two main parameters: the mean (μ), which is the central tendency of the distribution, and the standard deviation (σ), which measures the amount of variation or dispersion of a set of values.
In conclusion, creating and understanding bell curves is a fundamental aspect of statistical analysis, offering insights into the distribution of data. Whether through theoretical calculations, practical applications with real data, or using statistical software, the ability to generate and interpret bell curves is essential for anyone working with data. By following the methods and steps outlined in this article, individuals can enhance their understanding and application of bell curves in their respective fields. We invite readers to share their experiences and questions regarding the creation and interpretation of bell curves, contributing to a broader discussion on the importance of statistical literacy in today's data-driven world.