Intro
The Spearman Rank Correlation Coefficient is a statistical measure that calculates the strength and direction of the relationship between two variables. It is a non-parametric test, meaning it doesn't require the data to be normally distributed, making it a useful tool for analyzing data that doesn't meet the assumptions of parametric tests. In this article, we will explore how to calculate the Spearman Rank Correlation Coefficient in Excel, its benefits, and its applications.
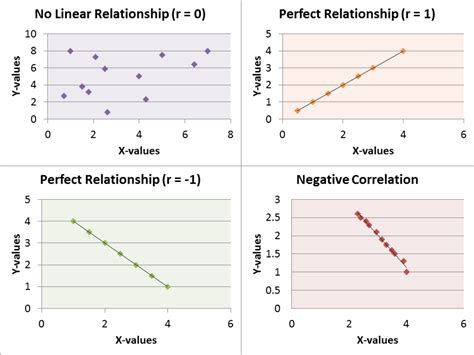
The Spearman Rank Correlation Coefficient is widely used in various fields, including finance, economics, and social sciences. It is particularly useful when dealing with ordinal data or data that has outliers, as it is more robust than other correlation coefficients. The coefficient ranges from -1 to 1, where 1 indicates a perfect positive correlation, -1 indicates a perfect negative correlation, and 0 indicates no correlation.
To calculate the Spearman Rank Correlation Coefficient in Excel, you can use the CORREL function or the RSQ function. However, these functions calculate the Pearson correlation coefficient, which is a parametric test. To calculate the Spearman Rank Correlation Coefficient, you need to use the following formula:
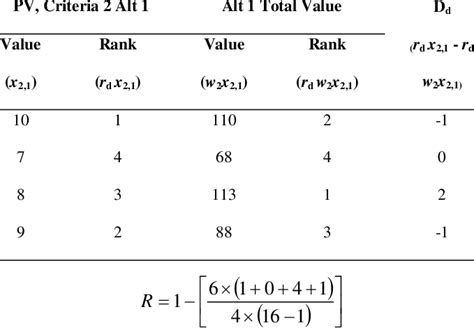
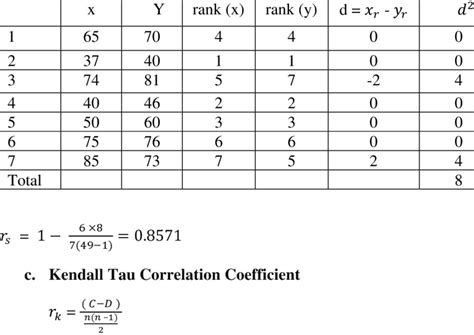
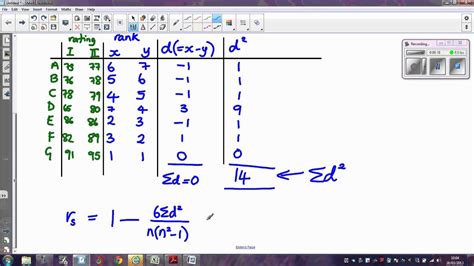
RS = 1 - (6 * Σd^2) / (n^3 - n)
where RS is the Spearman Rank Correlation Coefficient, d is the difference between the ranks of the two variables, and n is the number of observations.
Calculating Spearman Rank Correlation Coefficient in Excel
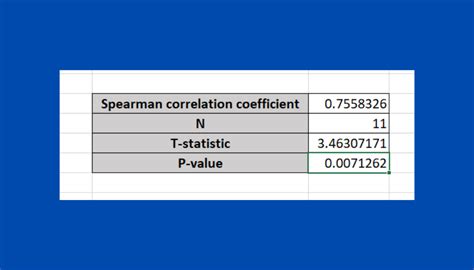
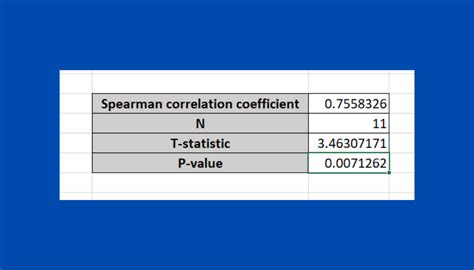
To calculate the Spearman Rank Correlation Coefficient in Excel, follow these steps:
- Enter your data into two columns, A and B.
- Rank the data in each column using the RANK function.
- Calculate the difference between the ranks of the two variables.
- Calculate the square of the differences.
- Calculate the sum of the squared differences.
- Calculate the Spearman Rank Correlation Coefficient using the formula: RS = 1 - (6 * Σd^2) / (n^3 - n)
You can also use the following Excel formula to calculate the Spearman Rank Correlation Coefficient:
=1-(6*SUM((RANK(A1:A10)-RANK(B1:B10))^2))/(10^3-10)
where A1:A10 and B1:B10 are the ranges of the two variables.
Benefits of Using Spearman Rank Correlation Coefficient

The Spearman Rank Correlation Coefficient has several benefits, including:
- It is a non-parametric test, making it suitable for analyzing data that doesn't meet the assumptions of parametric tests.
- It is robust to outliers, making it a useful tool for analyzing data with outliers.
- It is easy to calculate and interpret.
- It can be used to analyze ordinal data.
Applications of Spearman Rank Correlation Coefficient

The Spearman Rank Correlation Coefficient has several applications, including:
- Finance: to analyze the relationship between stock prices and trading volumes.
- Economics: to analyze the relationship between economic indicators, such as GDP and inflation.
- Social sciences: to analyze the relationship between social variables, such as education and income.
- Medicine: to analyze the relationship between medical variables, such as disease severity and treatment outcomes.
Interpreting the Results
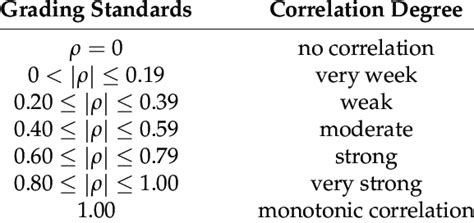
The results of the Spearman Rank Correlation Coefficient can be interpreted as follows:
- A coefficient of 1 indicates a perfect positive correlation.
- A coefficient of -1 indicates a perfect negative correlation.
- A coefficient of 0 indicates no correlation.
- A coefficient between 0 and 1 indicates a positive correlation.
- A coefficient between -1 and 0 indicates a negative correlation.
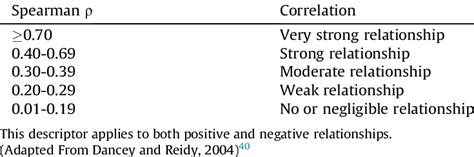
The strength of the correlation can be interpreted as follows:
- A coefficient between 0 and 0.3 indicates a weak correlation.
- A coefficient between 0.3 and 0.6 indicates a moderate correlation.
- A coefficient between 0.6 and 1 indicates a strong correlation.
Common Mistakes to Avoid

When using the Spearman Rank Correlation Coefficient, there are several common mistakes to avoid, including:
- Using the wrong formula or function.
- Failing to check for outliers.
- Failing to check for normality.
- Interpreting the results incorrectly.
Gallery of Spearman Rank Correlation Coefficient
Spearman Rank Correlation Coefficient Image Gallery
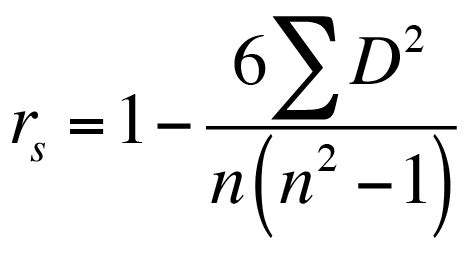


What is the Spearman Rank Correlation Coefficient?
+The Spearman Rank Correlation Coefficient is a statistical measure that calculates the strength and direction of the relationship between two variables.
What are the benefits of using the Spearman Rank Correlation Coefficient?
+The Spearman Rank Correlation Coefficient is a non-parametric test, making it suitable for analyzing data that doesn't meet the assumptions of parametric tests. It is also robust to outliers and easy to calculate and interpret.
How do I calculate the Spearman Rank Correlation Coefficient in Excel?
+To calculate the Spearman Rank Correlation Coefficient in Excel, you can use the following formula: RS = 1 - (6 * Σd^2) / (n^3 - n), where RS is the Spearman Rank Correlation Coefficient, d is the difference between the ranks of the two variables, and n is the number of observations.
What are the common mistakes to avoid when using the Spearman Rank Correlation Coefficient?
+Common mistakes to avoid when using the Spearman Rank Correlation Coefficient include using the wrong formula or function, failing to check for outliers, failing to check for normality, and interpreting the results incorrectly.
What are the applications of the Spearman Rank Correlation Coefficient?
+The Spearman Rank Correlation Coefficient has several applications, including finance, economics, social sciences, and medicine. It can be used to analyze the relationship between two variables, such as stock prices and trading volumes, or disease severity and treatment outcomes.
In conclusion, the Spearman Rank Correlation Coefficient is a useful statistical tool for analyzing the relationship between two variables. It is a non-parametric test, making it suitable for analyzing data that doesn't meet the assumptions of parametric tests. By following the steps outlined in this article, you can calculate the Spearman Rank Correlation Coefficient in Excel and interpret the results. We encourage you to share your experiences and ask questions in the comments section below. Additionally, if you found this article helpful, please share it with others who may benefit from it.