Intro
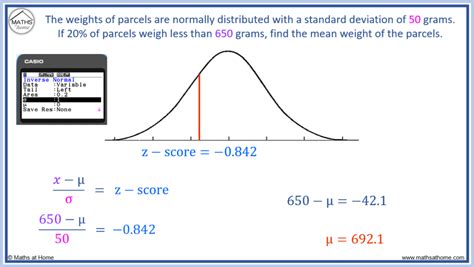
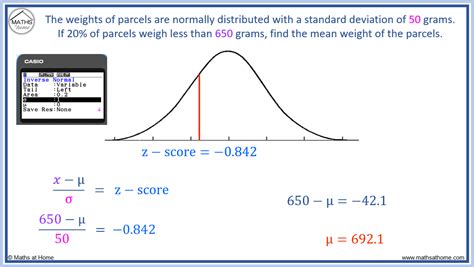
Understanding and working with z scores is a fundamental aspect of statistics, enabling the comparison of data points within a dataset to the average, or mean, value. The z score, also known as a standard score, indicates how many standard deviations an element is from the mean. A z score can be calculated using the formula: z = (X - μ) / σ, where X is the value of the element, μ is the mean of the dataset, and σ is the standard deviation. Mastering the calculation and interpretation of z scores is crucial for data analysis and statistical inference. Here are five practice tips to help improve your understanding and proficiency with z scores.
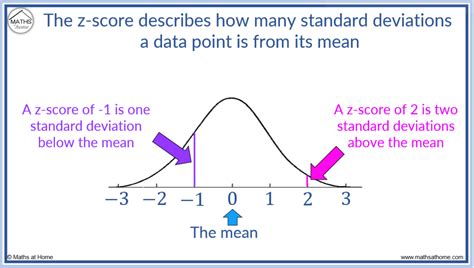
The first step in mastering z scores is to understand the concept thoroughly. This involves not just memorizing the formula but also grasping what the z score represents. For instance, a z score of 0 means the data point is equal to the mean, a positive z score indicates the data point is above the mean, and a negative z score signifies that the data point is below the mean. The greater the absolute value of the z score, the more extreme the data point is relative to the mean.
Moreover, practicing the calculation of z scores with various datasets is essential. Start with simple examples where the mean and standard deviation are given or easy to calculate. As you become more comfortable, move on to more complex datasets or scenarios where you might need to calculate the mean and standard deviation before finding the z score. Utilizing online calculators or spreadsheet software like Excel can also aid in practice, allowing you to quickly verify your manual calculations.
Understanding the Concept of Z Scores

To further enhance your skills, it's beneficial to learn how to interpret z scores in different contexts. For example, in psychology, z scores can be used to understand how an individual's score on a test compares to the average score of the population. In finance, z scores can be part of more complex calculations to assess the creditworthiness of companies. Understanding these applications can make the concept more engaging and relevant, motivating you to practice more.
Calculating Z Scores
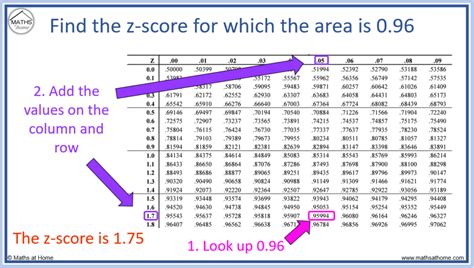
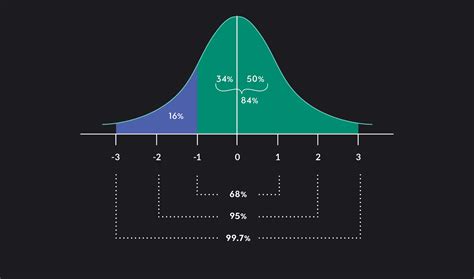
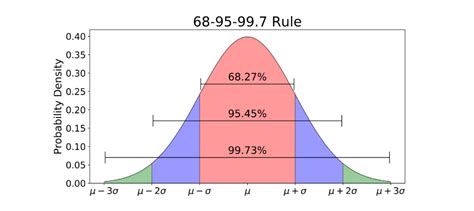
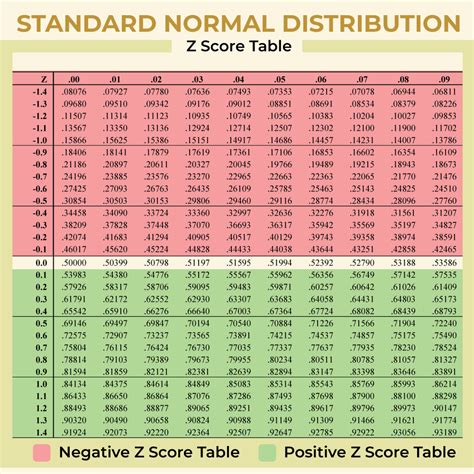
Another critical aspect of working with z scores is learning how to use them for hypothesis testing and confidence intervals. This involves understanding the z distribution (standard normal distribution) and how to look up z scores in a z table to find probabilities. Practicing how to read a z table and calculate probabilities associated with different z scores is vital. This skill is essential for statistical inference, where you might need to determine if an observed difference is statistically significant.
Interpreting Z Scores
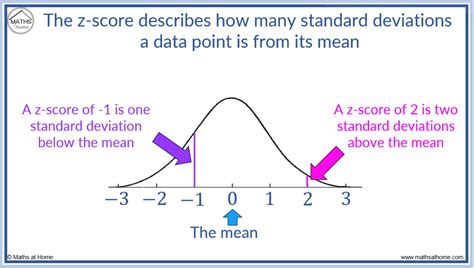
Lastly, applying z scores to real-world problems can make the concept more tangible and interesting. Look for scenarios in your daily life or in the news where z scores could be applied, such as understanding election polling results, analyzing stock performance, or evaluating the effectiveness of a new drug. By seeing the practical applications of z scores, you can better appreciate their utility and be more motivated to practice and master the concept.
Applying Z Scores in Real-World Scenarios

In addition to these tips, utilizing online resources such as video tutorials, practice quizzes, and interactive statistical software can provide a comprehensive learning experience. These resources can offer step-by-step explanations, examples, and exercises that cater to different learning styles and preferences.
Utilizing Online Resources for Z Score Practice

For those interested in a more structured approach, enrolling in a statistics course or workshop can provide a systematic way to learn about z scores and other statistical concepts. These courses often include practice sessions, assignments, and feedback from instructors, which can be invaluable for improving understanding and proficiency.
Enrolling in Statistics Courses

Furthermore, joining online communities or forums dedicated to statistics and data analysis can connect you with peers and professionals who can share insights, resources, and advice on learning and applying z scores. These communities can be a great place to ask questions, share knowledge, and learn from the experiences of others.
Joining Online Communities for Statistics Learners

In conclusion, mastering z scores requires a combination of understanding the concept, practicing calculations, interpreting results, applying to real-world scenarios, and utilizing various learning resources. By following these practice tips and staying committed to learning, you can enhance your proficiency in working with z scores and improve your overall statistical analysis skills.
Gallery of Z Score Applications
Z Score Applications Gallery
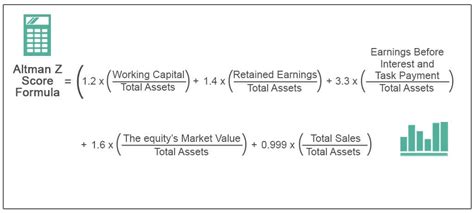
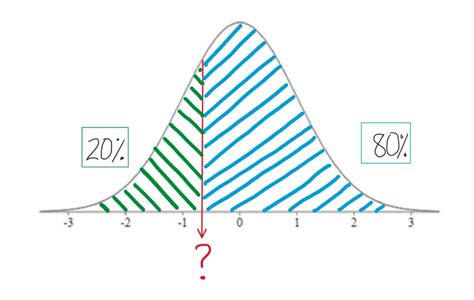


What is the formula for calculating a z score?
+The formula for calculating a z score is z = (X - μ) / σ, where X is the value of the element, μ is the mean of the dataset, and σ is the standard deviation.
How do I interpret a z score?
+A z score indicates how many standard deviations an element is from the mean. A positive z score means the element is above the mean, a negative z score means it is below the mean, and a z score of 0 means it is equal to the mean.
What are some real-world applications of z scores?
+Z scores have applications in finance, psychology, data analysis, business, research, statistics, economics, and academics, among other fields, to compare and understand data points relative to the average.
How can I practice calculating and interpreting z scores?
+You can practice by using online calculators, working through examples in textbooks or online resources, and applying z scores to real-world scenarios or datasets.
Why are z scores important in statistics?
+Z scores are important because they allow for the comparison of data points from different datasets and provide a way to understand how extreme a data point is relative to the mean, which is crucial for statistical inference and analysis.
We hope this comprehensive guide to z scores has been informative and helpful. Whether you are a student looking to understand statistical concepts better, a professional aiming to improve your data analysis skills, or simply someone interested in statistics, mastering z scores can open up new avenues for understanding and working with data. If you have any questions, need further clarification on any of the points discussed, or would like to share your experiences with z scores, please do not hesitate to comment below. Your engagement and feedback are invaluable to us, and we look forward to hearing from you.