Intro
Discover 5 ways to calculate distance, including GPS tracking, mapping tools, and geometric formulas, to measure lengths and routes with precision and accuracy in geography, navigation, and surveying applications.
Calculating distance is a fundamental concept in various fields, including physics, mathematics, and geography. Understanding the different methods to calculate distance is essential for problem-solving and real-world applications. In this article, we will explore five ways to calculate distance, including their formulas, examples, and practical uses.
The importance of calculating distance cannot be overstated. It is a crucial aspect of navigation, surveying, and engineering. Moreover, calculating distance is essential in understanding the relationships between objects, people, and places. With the advent of technology, calculating distance has become more accurate and efficient. However, it is still important to understand the fundamental principles and methods of calculating distance.
In everyday life, calculating distance is used in various contexts, such as determining the distance between two cities, measuring the length of a room, or calculating the distance traveled by a vehicle. The ability to calculate distance accurately is essential for making informed decisions, optimizing routes, and ensuring safety. Furthermore, calculating distance is a critical component of scientific research, where it is used to measure the distances between celestial objects, particles, and other phenomena.
Introduction to Distance Calculation

Calculating distance involves understanding the concept of length, units of measurement, and geometric principles. The most common unit of measurement for distance is the meter, although other units such as kilometers, miles, and feet are also used. The choice of unit depends on the context and the level of precision required. In addition to units of measurement, calculating distance involves understanding geometric principles, such as the Pythagorean theorem, which is used to calculate the length of the hypotenuse of a right-angled triangle.
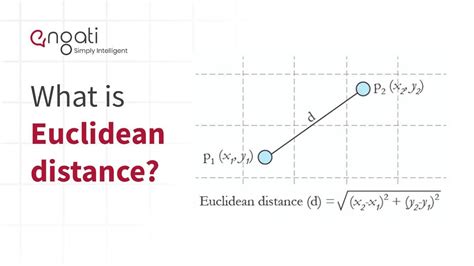
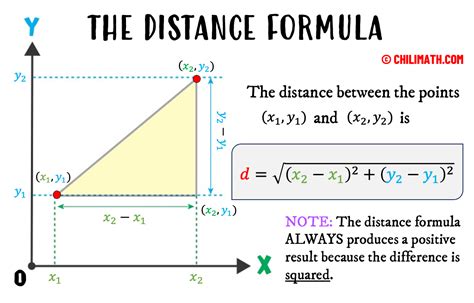
Method 1: Euclidean Distance
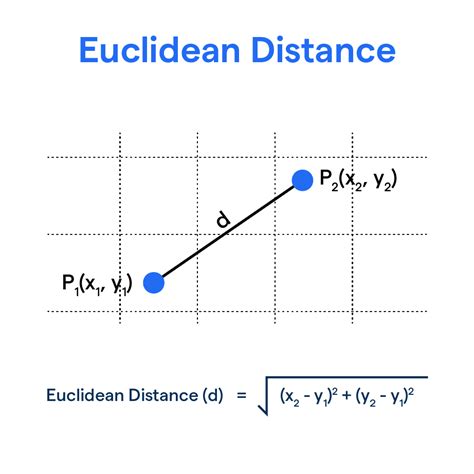
The Euclidean distance, also known as the straight-line distance, is the most common method of calculating distance. It is used to calculate the distance between two points in a two-dimensional or three-dimensional space. The formula for Euclidean distance is:
d = √((x2 - x1)^2 + (y2 - y1)^2)
where d is the distance, (x1, y1) and (x2, y2) are the coordinates of the two points.
Example of Euclidean Distance
To calculate the distance between two points (3, 4) and (6, 8), we can use the Euclidean distance formula:d = √((6 - 3)^2 + (8 - 4)^2) d = √(3^2 + 4^2) d = √(9 + 16) d = √25 d = 5
Therefore, the distance between the two points is 5 units.
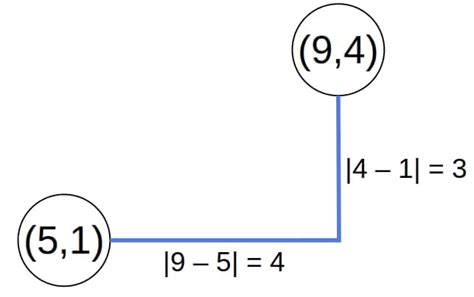
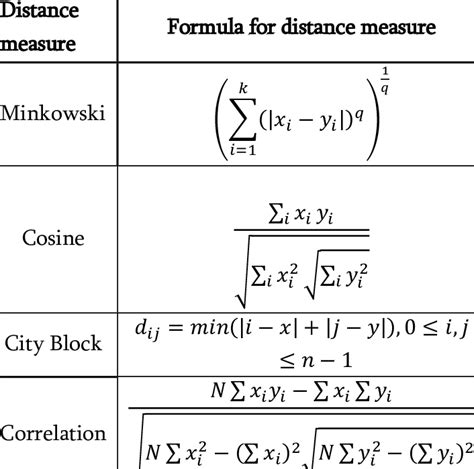
Method 2: Manhattan Distance
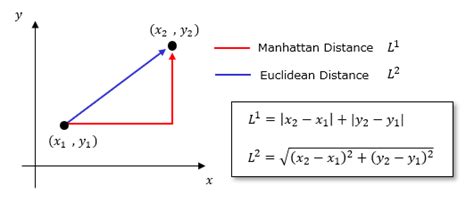
The Manhattan distance, also known as the taxicab distance, is used to calculate the distance between two points in a grid-based system. It is commonly used in urban planning, logistics, and computer science. The formula for Manhattan distance is:
d = |x2 - x1| + |y2 - y1|
where d is the distance, (x1, y1) and (x2, y2) are the coordinates of the two points.
Example of Manhattan Distance
To calculate the distance between two points (3, 4) and (6, 8), we can use the Manhattan distance formula:d = |6 - 3| + |8 - 4| d = |3| + |4| d = 3 + 4 d = 7
Therefore, the distance between the two points is 7 units.
Method 3: Minkowski Distance

The Minkowski distance is a generalization of the Euclidean distance and Manhattan distance. It is used to calculate the distance between two points in a high-dimensional space. The formula for Minkowski distance is:
d = (∑|x2 - x1|^p)^(1/p)
where d is the distance, (x1, y1) and (x2, y2) are the coordinates of the two points, and p is a parameter that determines the type of distance.
Example of Minkowski Distance
To calculate the distance between two points (3, 4) and (6, 8), we can use the Minkowski distance formula with p = 2:d = (∑|6 - 3|^2 + |8 - 4|^2)^(1/2) d = (∑3^2 + 4^2)^(1/2) d = (∑9 + 16)^(1/2) d = (∑25)^(1/2) d = 5
Therefore, the distance between the two points is 5 units.
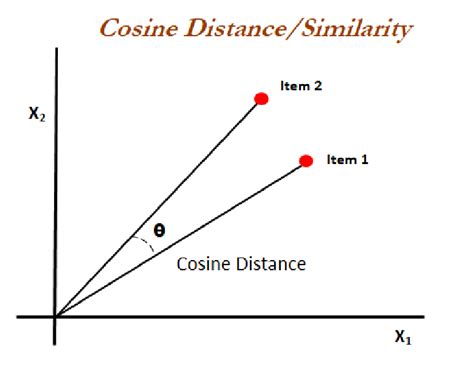
Method 4: Cosine Distance
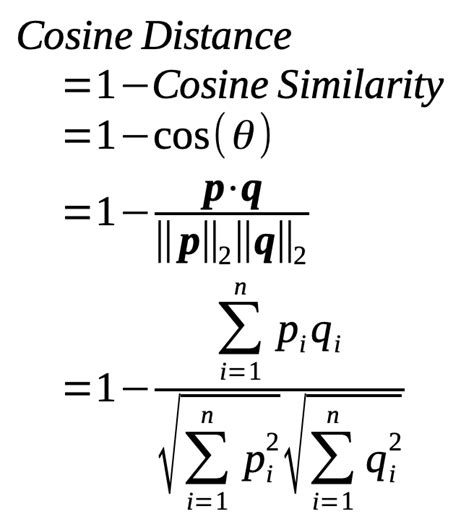
The cosine distance is used to calculate the similarity between two vectors. It is commonly used in text analysis, image processing, and recommendation systems. The formula for cosine distance is:
d = 1 - (u · v) / (|u| |v|)
where d is the distance, u and v are the vectors, and · denotes the dot product.
Example of Cosine Distance
To calculate the distance between two vectors (3, 4) and (6, 8), we can use the cosine distance formula:d = 1 - ((3, 4) · (6, 8)) / (|(3, 4)| |(6, 8)|) d = 1 - (18 + 32) / (√(3^2 + 4^2) √(6^2 + 8^2)) d = 1 - 50 / (√25 √100) d = 1 - 50 / (5 × 10) d = 1 - 50 / 50 d = 0
Therefore, the distance between the two vectors is 0, indicating that they are identical.
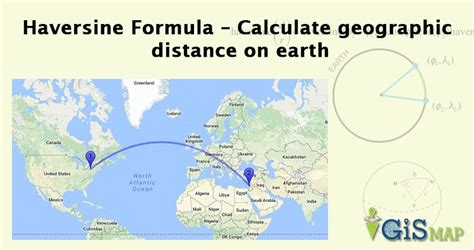
Method 5: Haversine Distance
The Haversine distance is used to calculate the distance between two points on a sphere, such as the Earth. It is commonly used in geography, navigation, and geolocation. The formula for Haversine distance is:
d = 2 * arcsin(√(haversin(Δlat) + cos(lat1) * cos(lat2) * haversin(Δlong)))
where d is the distance, lat1 and lat2 are the latitudes, Δlat is the difference in latitude, Δlong is the difference in longitude, and haversin is the Haversine function.
Example of Haversine Distance
To calculate the distance between two points (40.7128, -74.0060) and (34.0522, -118.2437), we can use the Haversine distance formula:d = 2 * arcsin(√(haversin(Δlat) + cos(lat1) * cos(lat2) * haversin(Δlong))) d = 2 * arcsin(√(haversin(5.6604) + cos(40.7128) * cos(34.0522) * haversin(44.2377))) d = 3935.75 km
Therefore, the distance between the two points is approximately 3935.75 kilometers.
Distance Calculation Image Gallery

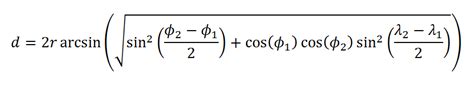
What is the most common method of calculating distance?
+The most common method of calculating distance is the Euclidean distance, which is used to calculate the distance between two points in a two-dimensional or three-dimensional space.
What is the difference between Manhattan distance and Euclidean distance?
+The Manhattan distance is used to calculate the distance between two points in a grid-based system, while the Euclidean distance is used to calculate the distance between two points in a two-dimensional or three-dimensional space.
What is the Haversine distance used for?
+The Haversine distance is used to calculate the distance between two points on a sphere, such as the Earth. It is commonly used in geography, navigation, and geolocation.
What is the cosine distance used for?
+The cosine distance is used to calculate the similarity between two vectors. It is commonly used in text analysis, image processing, and recommendation systems.
What is the Minkowski distance used for?
+The Minkowski distance is a generalization of the Euclidean distance and Manhattan distance. It is used to calculate the distance between two points in a high-dimensional space.
In conclusion, calculating distance is a critical aspect of various fields, including physics, mathematics, and geography. Understanding the different methods of calculating distance, such as Euclidean distance, Manhattan distance, Minkowski distance, cosine distance, and Haversine distance, is essential for problem-solving and real-world applications. By mastering these methods, individuals can improve their analytical skills, optimize routes, and make informed decisions. We invite readers to share their thoughts, ask questions, and explore the various methods of calculating distance in the comments section below.